
"Mechanics is the paradise of the mathematical sciences because by means of it one comes to the fruits of mathematics."
Leonardo da Vinci

William Leybourn, (1626-1719). Image courtesy National Oceanic & Atmospheric Administration, photographed by Sean Linehan.
The inspiration for this article comes from a slightly unusual source: The Proceedings of the Old Bailey from April 18th 1694. On this particular day 29 death sentences were passed at the court house, as well as numerous orders for brandings; there would have been 30 death sentences had not one lady's pregnancy saved her — she had successfully "pleaded her belly". The business part of the document ends with a list of the 29 unfortunates and continues to another list; this time of advertisements. Surprising though it may seem, advertisements for anything from quack remedies to religious texts formed an important part of the court proceedings between the 1680s and the 1750s. On April 18th 1694 the second item on the list was an advert for a book:
Pleasure with Profit: Consisting of Recreations of divers kinds, viz. Numerical, Geometrical, Mathematical, Astronomical, Arithmetical, Cryptographical, Magnetical, Authentical, Chymical, and Historical. Published to Recreate Ingenious Spirit, and to induce them to make further scrutiny how these (and the like) Sublime Sciences. And to divert them from following such Vices, to which Youth (in this Age) are so much inclin'd. By William Laybourn, Philomathes.
If the author of these lines is to be believed, then those who were tried in the docks that day may well have been spared their gruesome fate, had they only been given access to this work. We will touch on only a small part of it ourselves: to be precise, pages 12 and 13.
A detail of page 12 of Pleasure with Profit.
William Leybourn (1626-1719) (alias Oliver Wallingby) was in his time a distinguished land and quantity surveyor (although he began his working life as a printer). Such was his prestige, he was frequently employed to survey the estates of gentlemen, and he also helped to survey the remnants of London after the great fire of 1666. A prolific and eclectic author, his work The Compleat Surveyor, which was first published in 1653 and ran to five editions, is regarded as a classic of its kind and (in collaboration with one Vincent Wing) the 1649 volume Urania Practica, was the first book in English devoted to astronomy.
In 1694 he had published the recreational volume Pleasure with Profit. It contained a delightful mechanical puzzle, attributed to one "J.P.", which has become known as the Uphill Roller.
Pages 12 and 13 of the book detail the construction of a double cone and two inclined rails along which the cone can roll — uphill! His final paragraph explains the paradox: even though the cone does ascend the slope, its centre of gravity will actually move downwards, if the experiment is set up in the right way. Although one's senses might be confounded, the law of gravity is not.
This animation shows a virtual uphill roller in action. In the animation below you can see the downward movement of the centre of gravity of the double cone.
Before we examine his explanation, we will look at the matter through modern eyes, using elementary trigonometry. The experiment consists of two inclined rails and a double cone. The cone will roll "uphill" resting on the top surfaces of the two rails.
Figure 1 shows a vertical section of the set-up. The inclined line represents the top surfaces of the rails. The bottom end of the slope, shown at the left-hand side of figure 1, is at a distance a from the ground. The top end of the slope, on the right-hand side of figure 1, is at a distance b from the ground. The figure also shows the cross-section of the double cone after it has rolled some way up the slope. The point in the middle of this cross section is the double cone's centre of gravity, which we call G. The angle of inclination of the rails is $\alpha.$ Imposing a coordinate system on this plane as shown, we give the point G the coordinates (x,y). As the double cone rolls up the rails, its centre of gravity G moves along a path given by some equation y = f(x). Our aim is to find this equation.
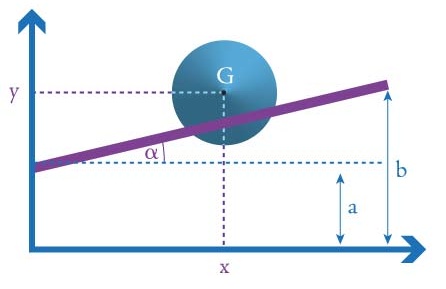
Figure 1
Figure 2 shows the view from the front, in other words from the point where the two rails meet. We see the cone as if it had been sliced vertically and lengthwise. Again we see the centre of gravity G, as well as the points P and Q where the top surfaces of the two rails meet the double cone. The points G1, P1 and Q1 are the projections of these three points to the ground. The angle $\gamma$ is half of the angle at the apex of the cone.
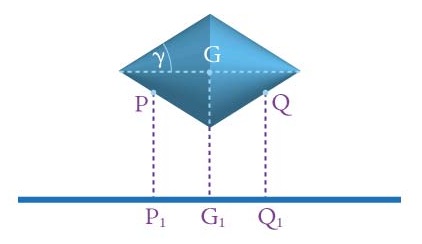
Figure 2
Figure 3 shows the projection of the whole set-up to the floor. The diamond shape is the shadow the double cone casts on the floor and the two lines emanating from the points P1 and Q1 are the shadows cast by the two rails. They meet at the point O and at an angle 2β. As before, the points G1, P1 and Q1 are the projections of G, P and Q.
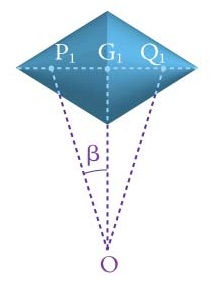
Figure 3
With the coordinate system from figure 1 in place we can find the equation of the path of the centre of gravity of the double cone as it rolls up the slope. For convenience we write XY for the straight line segment running from a point X to a point Y.
First consider figure 3. The distance between O and G1 is precisely the x-coordinate of the point G. Using basic trigonometry we have that $$tan(\beta) = \frac{P_1 G_1}{x}= \frac{P_1 Q_1}{2x}.$$
Since P1Q1 = PQ we get $$PQ = 2x \tan(\beta).$$
Now let's take the front view from figure 2. Write S for the point that lies on the line from G to G1 at the same height as P and write R for the apex of the cone which lies on the line from G to G1. See figure 4.
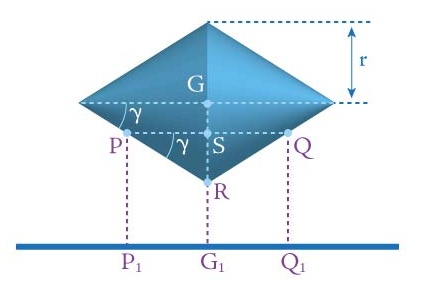
Figure 4
Then $\frac{RS}{SP} = \tan(\gamma)$ so $RS = SP \tan{\gamma} = \frac{PQ \tan(\gamma)}{2}.$ We know that $PQ = 2x\tan(\beta)$, so $$RS = SP \tan(\gamma) = \frac{PQ \tan(\gamma)}{2} = x \tan(\beta) \tan(\gamma).$$
Now the height y of G is SG1 + SG. For the second part we have SG = r-RS, where 2r is the thickness of the double cone at its centre (see figure 4). So $$SG = r - RS = r - x\tan(\beta)\tan(\gamma).$$ This gives $$ y = SG_1 + SG = SG_1 + (r - x \tan(\beta)\tan(\gamma)).$$ Figure 5 below shows the same view as figure 1. Noting that the point G1 is at distance x from the origin of the coordinate system, we get $(SG_1 - a)/x = \tan(\alpha)$ and hence $SG_1 - a = x \tan(\alpha)$.
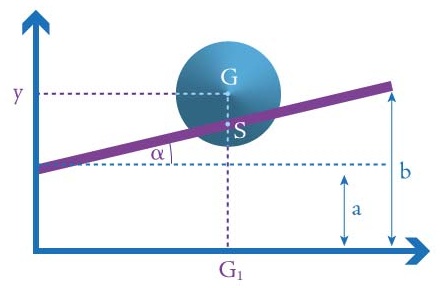
Figure 5
Therefore we have $$ y=(a+x\tan(\alpha))+(r-x\tan(\beta) \tan(\gamma))=a+r+x(\tan(\alpha)-\tan(\beta)\tan(\gamma)). $$
The path of the centre of gravity of the cone is, then, the straight line $$y = a + r + x(\tan(\alpha) - \tan(\beta) \tan(\gamma)),$$ which has the gradient $\tan(\alpha) - \tan(\beta) \tan(\gamma)$. For the motion to be possible this straight line has to be sloping downward, as the centre of gravity can only move downhill. This means that the gradient has to be negative, and so the defining condition for the paradox to exist is that $$\tan(\alpha) < \tan(\beta)\tan(\gamma).$$
Of course, to properly appreciate the paradox a physical model is needed. The author's model (made by his long-term friend Brian Caswell) has: $$\alpha = 4.6, \beta = 15.3, \gamma = 25.4,$$ measured in degrees, from which it is plain that the inequality holds.
An excerpt from Leybourn's recipe for an uphill roller
The things necessary for this Experiment are, First, A Roller of Wood [...] of two Cones (or Sugar Loaves). Let the thickness in the middle be about 5 or 6 Inches, the length [of the cone] about 3 times the thickness. [...] You must provide two straight smooth Rulers about a Yard in length, and strong enough to bear the weight of the Roller. Lastly, you must have three pieces of Wood to support the ends of the rulers; the first about two or three inches thick [to support the rulers at the bottom of the slope]; the other two [to support the rulers at the top of the slope] must be thicker than the first by somewhat less than half the diameter of the ruler.
Leybourn's recipe
Now that we have a clear criterion to use, we can look more closely at Leybourn's instructions for building an uphill roller (which we've reproduced on the right) and check that they really do give rise to angles that satisfy the required relationships. The instructions specify that each of the cones that make up the double cone should be between 5 and 6 inches in thickness, so taking the upper limit of 6 we get r=3. The length of each of the two cones is to be three times its thickness, so it is 9. The rails are to be one yard in length, and since one yard is 36 inches, the length of the slope is 36.
The blocks supporting the end of the slope should be thicker than those supporting the beginning of the slope by "somewhat less" than half the diameter of the cone, in other words by less than r (as marked in the left-hand diagram in figure 6 below). We can choose the thicknesses of the blocks so that their difference is less than, but very close to r. Then the difference in height between the bottom of the slope and the top of the slope, b - a, is roughly equal to r.
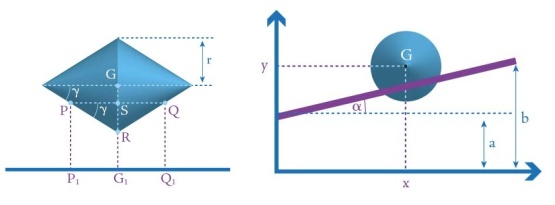
Figure 6
From this and the right-hand diagram in figure 6, we now deduce that $$\sin(\alpha) = \frac{b-a}{length \; of \; slope} = \frac{3}{36} = \frac{1}{12}.$$ This means that $\alpha$ is an angle of a right-angled triangle with a hypothenuse of length 12 and the side opposite $\alpha$ having length 1. Using Pythagoras's Theorem we can work out the third side of this triangle to have length $\sqrt{12^2 - 1^2} = \sqrt{143}$ and therefore evaluate $$ \cos(\alpha) = \frac{\sqrt{143}}{12}, \tan(\alpha) = \frac{1}{\sqrt{143}}.$$

Figure 7
Now let's turn to the angle β. The right hand diagram in figure 6 shows that the sloped rail and the dotted horizontal line form a right angled triangle with an angle $\alpha$ between them. The slope is the hypothenuse of this triangle, and the dotted line has the same length as the shadow the rail casts on the ground, so $$\cos(\alpha) = \frac{length \; of \; shadow \;of \; rail}{length\; of \; slope} = \frac{length \; of \; shadow \; of \; rail}{36},$$ so the length of the rail's shadow is equal to $36 \cos(\alpha)$.
At the end of the cone's journey, the point P1, shown in figure 7, will be at the left-hand apex of the double cone, and its distance to G will be the length of one cone, which is 9. This gives $$\sin(\beta) = \frac{length \; of \; one \; cone}{length \; of \; shadow \;of \; rail} = \frac{9}{36 \cos(\alpha)} = \frac{3}{\sqrt{143}}.$$ Again we have a right angled triangle whose third side is $ \sqrt{143 - 9} = \sqrt{134}$, making $\cos(\beta) = \frac{\sqrt{134}}{\sqrt{143}}$, so $\tan(\beta) = \frac{3}{\sqrt{134}}$.

Figure 8
From figure 8 we get that $$\tan(\gamma) = \frac{r}{length \; of \; one \; cone} = \frac{3}{9} = \frac{1}{3}.$$
In summary, Leybourn's instructions reduce to: $$\tan(\alpha) = \frac{1}{\sqrt{143}}, \tan(\beta) = \frac{3}{\sqrt{134}}, \tan(\gamma) = \frac{1}{3}$$ our inequality requires that $$\frac{3}{\sqrt{134}} \times 1/3 > \frac{1}{\sqrt{143}}$$ or that 143 > 134 — which indeed it is! (Using the same analysis, his lower limit of 5 inches requires that 5159>4934).
With the mystery of the uphill roller explained we will leave the reader with the following sentiment expressed in the book, with which we whole-heartedly agree:
But leaving those of the Body, I shall proceed to such Recreations as adorn the Mind; of which those of the Mathematicks are inferior to none.
About the author
