
This article is a runner up in the general public category of the Plus new writers award 2008
"The universe, which others call the Library, is composed of an indefinite and perhaps infinite number of hexagonal galleries..."
Thus begins The Library of Babel, a short story by the Argentinean writer Jorge Luis Borges.

Later on, he recalls that "Like all men of the Library, I have travelled in my youth; I have wandered in search of a book, perhaps the catalogue of catalogues." And he adds, "There are five shelves for each of the hexagon's walls; each shelf contains thirtyfive books of uniform format; each book is of four hundred and ten pages; each page, of forty lines, each line, of some eighty letters ..."

Sergey Brin, one of the two founders of Google. Image courtesy James Duncan Davidson/O'Reilly Media, Inc. Reproduced under Creative Commons Attribution 2.0.
Perhaps Borges was anticipating in his portentous library the vastness of the World Wide Web, and longing for the perfect librarian who could resolve the despair of a search. Alas, Borges died in 1986, three years before Tim Berners-Lee, working at the European Organization for Nuclear Research, launched the idea of the Web as an information conglomerate. Another nine years had to pass until in 1998 two graduate students at Stanford University, Sergei Brin and Larry Page, published The Anatomy of a Large-Scale Hypertextual Web Search Engine, where they introduced Google and revolutionised the design of Web search engines.
As Brin and Page tell in their article, google is a common spelling for googol, the name of the impossibly large number 10100. There is no doubt that Google, the search engine, and Google, the company, have both lived up to the expectations of their name. A single number can give us the proof:
This was the estimated market value of the company, in dollars, when it went public in 2004, and it is the approximate number of documents ranked by Google.

Larry Page, one of the two founders of Google. Image courtesy aweigend. Reproduced under Creative Commons Attribution 2.0.
For the sake of brevity, we will concentrate on how Google decides the relative importance of a page, ignoring all other aspects. But we must not forget that before doing any ranking, a Web search engine has to identify the public pages and it has to index them, so key words or phrases can be found easily.
The importance of being connected
Google judges the importance of a page on the basis of the importance of the pages linked to it. In this simple principle resides much of Google's success. Rather than using word of mouth, expert advice or other human interventions, Google lets the Web do the ranking, using the Web's own linking structure.
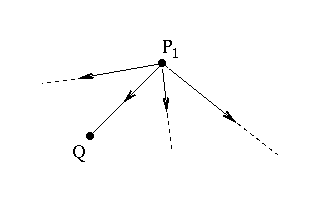
The alert reader might have noticed the troubling fact that our stated criterion did not really define what importance is. It merely referred the importance of one page to the importance of other pages. So, we ask now, how does Google quantify this notion of importance?
Although the full story of what Google does is not quite known, here is the gist of it: if the page $P_1$ has a total of, say, 10 links to other pages, among them the page $Q$, then $P_1$ will transfer one tenth of its importance to $Q$.
Now suppose that the pages that link to page $Q$ are $P_1$, $P_2$, etc, up to page $P_n.$ These pages are called the back links of $Q$. Write $I_1$, $I_2$, etc, for the importance of the pages $P_1$, $P_2$, etc. In the same way, write $l_1$, $l_2$, etc, for the total number of links on page $P_1$, $P_2$, etc. Then we can work out the importance of page $Q$ as $$I_Q = \frac{I_1}{l_1} + \frac{I_2}{l_2} + ... + \frac{I_n}{l_n}.$$ So the importance of the page $Q$ is a \emph{weighted sum} of the importance of its back links.
To make more apparent how this formula works for a whole web, first label all the pages in the web by $P_1$, $P_2$, $P_3$, etc. Now build an array $H$ of numbers, in which the entry corresponding to the $ith$ row and $jth$ column is $$\frac{1}{l_j}$$ if page $P_j$ has a link to page $P_i$ and 0 if it doesn't. For example, the mini web
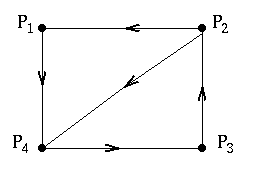
has the array $$H = \left(\begin{array}{cccc} 0 & 1/2 & 0 & 0 \\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \\ 1 & 1/2 & 0 & 0 \end{array}\right).$$ Here the second entry in the first row is 1/2 because $P_2$ links to $P_1$ and has a total of two links. The array for
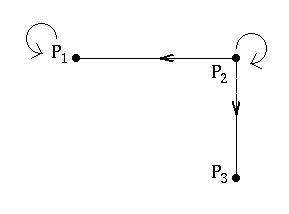
is $$H = \left(\begin{array}{ccc} 1 & 1/3 & 0\\ 0 & 1/3 & 0\\ 0 & 1/3 & 0\end{array}\right).$$ This array is called the \emph{link matrix} of the web. For a web with $n$ pages it has exactly $n$ rows and $n$ columns.
Now let's pretend for a moment that we know the importance of each page and collect this information in a vector $$I = (I_1, I_2, ..., I_n)$$ of length $n$. An area of mathematics called \emph{linear algebra} tells us how to multiply a matrix by a vector. The result is also a vector. And it turns out that the product of our link matrix $H$ and the importance vector $I$ is equal to ... the vector $I$ itself! In other words we have $$HI = I.$$ (See here for an easy explanation.)
This is independent of the nature and size of the web, and of the actual values in the vector $I$ $-$ it always works because of the way we have defined them in general terms.
And here comes the crucial bit: linear algebra also provides the tools to solve the matrix equation $$HI = I,$$ to find the vector $I$ when $H$ is known and $I$ is not. It's linear algebra, rather than human assessment, that teases the importance of each page out of the web's link structure.
The property that $HI = I$ is mathematically described by saying that the importance vector is an \emph{eigenvector} of the link matrix, with \emph{eigenvalue} 1. (In general, a vector $V$ is an eigenvector of $H$ with eigenvalue $k$, if $H$ multiplied by $V$ produces the vector $V$ with each entry multiplied by $k$.)
Going back to our first mini web, the eigenvector we are looking for turns out to be $$(1/7,2/7, 2/7, 2/7).$$ So, Google tells us that the first page is half as important as the other three pages, which are equally ranked. This is not a conclusion we could have drawn by just staring at our mini web, and it signals how cryptic the transference of importance between pages can be. But in the end, all that counts is Google's ability to turn out the good stuff at the top of the list.
We should point out here that the equation $HI = I$ remains true if we multiply each entry of the vector $I$ by some number $a$. This means that there are infinitely many eigenvectors of eigenvalue 1. It is customary to choose the only one whose entries add up to 1, as is the case in our example here. The zero vector always satisfies the above equation, but it will not give us any information about the relative importance of the pages. Therefore we always look for a non-zero eigenvector.
Problem rankings
Much remains to be said and done if instead of our mini web we are dealing with the real Web. Finding the eigenvectors of a matrix with 25,000,000,000 rows and columns is a tremendous task. There is not much hope for finding these eigenvectors in a reasonable time, and instead one aims at capturing good enough approximations. Other mathematical techniques are brought into this effort. We will not dwell in the details, because more challenges lie ahead.
You see, so far we have taken for granted that if we put enough mathematics to work, we will be able to find exactly one solution to our problem. But this might not be true, regardless of the size of the web. Disconnected webs, such as
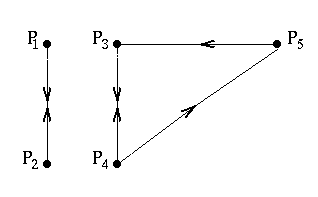
are bad news. The link matrix $$\left(\begin{array}{ccccc}0&1&0&0&0\\ 1&0&0&0&0\\ 0&0&0&1/2&1\\ 0&0&1&0&0\\ 0&0&0&1/2&0\end{array}\right)$$ has two eigenvectors with eigenvalue 1 that are not multiples of each other, for example $(1, 1, 0, 0, 0)$ and $(0, 0, 2, 2, 0)$. Here it is not possible to find a unique importance vector.
The disconnection of this web is reflected in the block structure of the link matrix. It has two sub-matrices $$\left(\begin{array}{cc}0&1\\1&0\end{array}\right)$$ in the upper left corner, and $$\left(\begin{array}{ccc}0&1/2&1\\1&0&0\\0&1/2&0\end{array}\right)$$ in the lower right corner. Both of these submatrices have eigenvectors with eigenvalue 1. The vector $(1, 1)$ is an eigenvector for the first submatrix, while $(2, 2, 0)$ is an eigenvector for the second. Filling in with zeros, we obtain the eigenvectors $(1, 1, 0, 0, 0)$ and $(0, 0, 2, 2, 0)$ for the full link matrix. It is not surprising that a disconnected web will not have a well defined importance vector, because in our scheme of things, it does not make much sense to compare pages that are not linked at all.
In spite of this problem, Google still manages to come up with a sensible solution. It does it by creating a new matrix that combines the original link matrix $H$ and the matrix $A$ for which all the entries are equal to 1/5 (because there are 5 pages in our web). The new matrix is calculated as $$(1-m)H + mA,$$ for some number $m$ between 0 and 1. This means "multiply all entries of $H$ by $1-m$ and all entries of $A$ by $m$ and then add the corresponding entries of the two matrices". The choice $m = 0$ brings us back to the original link matrix $H$, while $m = 1$ gives us $A$, the link matrix for a web where each of the five pages is a back link for all the pages:
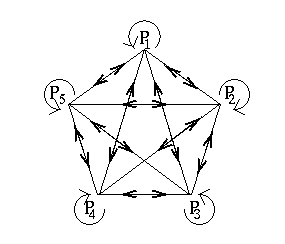
Google does not publicise its recent choices for $m$, but it is known that in the past it has used the value $m = 0.15$, which gives us the combined matrix $$\left(\begin{array}{ccccc}0.03&0.88&0.03&0.03&0.03\\0.88&0.03&0.03&0.03&0.03 \\0.03 &0.03&0.03&0.455&0.88\\0.03&0.03&0.88&0.03&0.03\\ 0.03&0.03&0.03&0.455&0.03\end{array}\right)$$ This matrix does have eigenvectors of eigenvalue 1 that are, approximately, all the non-zero multiples of the vector $(0.43895, 0.43895, 0.52331, 0.51066, 0.28287)$. This means that the importance vector is now uniquely defined.
Another problem that might arise is that the link matrix has no non-zero eigenvectors at all. This can occur when there are dangling pages, which do not have any back links. But thankfully, linear algebra provides the techniques for dealing with these cases too. In the real Web, one would have to keep track of both, dangling pages and disconnected pages.
All the steps we have described, together with its modifications and more, constitute the so-called PageRank algorithm. We can think of it as a mathematical evaluation of the Web. Google runs its PageRank algorithm monthly, counteracting in this way the ever changing nature of the Web.
I do not want to leave you with the idea that Google is the only path to a rewarding Web search. Other successful search engines do exist, but Google still enjoys a lion's share of the market, inspiring millions of fans to search the Web with confidence. One of these fans, the cartoonist Gerry Trudeau, describes Google as "the Swiss Army knife of information retrieval".
About the author

Josefina (Lolina) Alvarez was born in Spain. She earned a doctorate in mathematics from the University of Buenos Aires in Argentina, and is currently a professor of mathematics at New Mexico State University in the United States. Her research interests lie in the areas of functional and harmonic analysis. She is on the editorial board of Matematicalia and writes the column What if...?. She likes to hike, and with husband Larry and dogs Brandywine and Sofia, she has walked many kilometres along the beautiful trails of New Mexico and elsewhere. You can read more about her on her website.
Plus would like to thank the London Mathematical Society and the Maths, Stats and Operational Research Network, as well as the journal Nature for their kind support of this competition.
 |
 |