
This article is the winner of the schools category of the Plus new writers award 2008. Students were asked to write about the life and work of a mathematician of their choice.
"But the best problem I ever found, I found in my local public library."

Andrew Wiles. Image © C. J. Mozzochi, Princeton N.J.
There is a problem that not even the collective mathematical genius of almost 400 years could solve. When the ten-year-old Andrew Wiles read about it in his local Cambridge library, he dreamt of solving the problem that had haunted so many great mathematicians. Little did he or the rest of the world know that he would succeed...
"Here was a problem, that I, a ten-year-old, could understand and I knew from that moment that I would never let it go. I had to solve it."

Pierre de Fermat
The story of the problem that would seal Wiles' place in history begins in 1637 when Pierre de Fermat made a deceptively simple conjecture. He stated that if $n$ is any whole number greater than 2, then there are no three whole numbers $a$, $b$ and $c$ other than zero that satisfy the equation \\ \\ $a^n + b^n = c^n.$ \\ \\ (Note that if $n = 2$, then whole number solutions do exist, for example $a=3$, $b=4$ and $c=5$.)
Fermat claimed to have proved this statement but that the "margin [was] too narrow to contain" it. It is the seeming simplicity of the problem, coupled with Fermat's claim to have proved it, which has captured the hearts of so many mathematicians.
"Then when I reached college, I realized that many people had thought about the problem during the 18th and 19th centuries and so I studied those methods."

Leonhard Euler
Andrew Wiles was born in Cambridge, England on April 11 1953. At the age of ten he began to attempt to prove Fermat's last theorem using textbook methods. He then moved on to looking at the work of others who had attempted to prove the conjecture. Fermat himself had proved that for n=4 the equation had no solution, and Euler then extended Fermat's method to n=3. The problem was that to prove the general form of the conjecture, it does not help to prove individual cases; infinity minus something is still infinity. Wiles had to try a different approach in order to solve the problem.
"However impenetrable it seems, if you don't try it, then you can never do it."
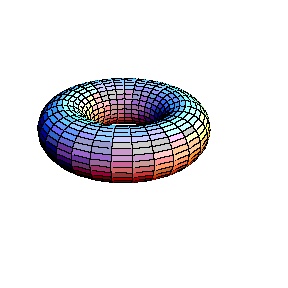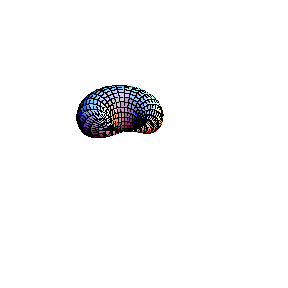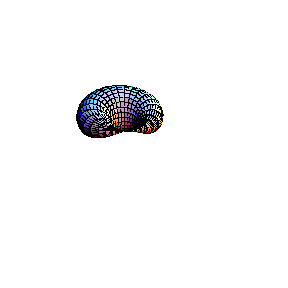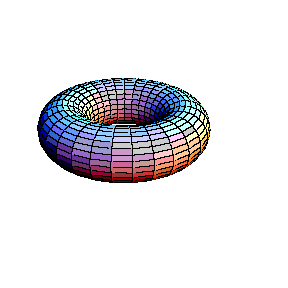
A family of elliptic curves. Animation courtesy Aleksandar T. Lipkovski.
Wiles earned a bachelors degree from Oxford University in 1974 and a PhD from Cambridge in 1980. It was while at Cambridge that he worked with John Coates on the arithmetic of elliptic curves. Elliptic curves are confusingly not much like an ellipse or a curve! They are defined by points in the plane whose co-ordinates $x$ and $y$ satisfy an equation of the form \\ \\ $y^2 = x^3 + \mu x + \lambda,$ \\ \\ where $\mu$ and $\lambda$ are constants, and they are usually doughnut-shaped. When Wiles began studying elliptic curves they were an area of mathematics unrelated to Fermat's last theorem. But this was soon to change. Since the 1950s the Taniyama-Shimura conjecture had stated that every elliptic curve can be matched to a modular form — a mathematical object that is symmetrical in an infinite number of ways. Then in the summer of 1986 Ken Ribet, building on work of Gerhard Frey, established a link between Fermat's last theorem, elliptic curves and the Taniyama-Shimura conjecture. By showing a link between these three vastly different areas Ribet had changed the course of Wiles' life forever.
"I was electrified. I knew that moment the course of my life was changing."
What Ribet had managed to show, and what Frey had intuited, was that if Fermat's last theorem were false, that is if there were three non-zero whole numbers $a$, $b$ and $c$, and a whole number $n$ greater than 2 so that $$a^n + b^n = c^n,$$ then this would have very special consequences for the elliptic curve $$y^2 = x(x-a^n)(x-b^n),$$ which is known as the Frey curve: this curve would be unrelated to a modular form. If such an elliptic curve existed, then the Taniyama-Shimura conjecture would be false. Looking at this from a different perspective we can see that if the Taniyama-Shimura conjecture could be proved to be true, then the curve could not exist, hence Fermat's last theorem must be true. So to prove Fermat's last theorem, Wiles had to prove the Taniyama-Shimura conjecture.
"You can't really focus yourself for years unless you have undivided concentration, which too many spectators would have destroyed"
Proving the Taniyama-Shimura conjecture was an enormous task, one that many mathematicians considered impossible. Wiles decided that the only way he could prove it would be to work in secret at his Princeton home. He still performed his lecturing duties at the university but no longer attended conferences or told anyone what he was working on. This led many to believe he had finished as a mathematician; simply run out of ideas. After six years working alone, Wiles felt he had almost proved the conjecture. But he needed help from a friend called Nick Katz to examine one part of the proof. No problems were found and the moment to announce the proof came later that year at the Isaac Newton Institute in Cambridge. There it was that in June 1993 Andrew Wiles announced his historic proof of Fermat's Last Theorem.
"It was so indescribably beautiful; it was so simple and elegant."

Andrew Wiles
Unfortunately for Wiles this was not the end of the story: his proof was found to contain a flaw. The flaw in the proof cannot be simply explained; however without rectifying the error, Fermat's last theorem would remain unsolved. After a year of effort, partly in collaboration with Richard Taylor, Wiles managed to fix the problem by merging two approaches. Both of the approaches were on their own inadequate, but together they were perfect. So it came to be that after 358 years and 7 years of one man's undivided attention that Fermat's last theorem was finally solved.
"I think I'll stop here."
About the author

Neil Pieprzak is currently in year 12 studying for his A levels at Notre Dame Sixth Form in Sheffield. His interest in this particular problem was sparked by reading the book Fermat's last theorem by Simon Singh, which gives a great insight into the history of the theorem for those who want to know more. Neil hopes to study maths at university in 2009, where he is looking forward to tackling some problems of his own. In his spare time he enjoys watching football and has a season ticket for Sheffield Wednesday Football Club.
Plus would like to thank the London Mathematical Society and the Maths, Stats and Operational Research Network, as well as the journal Nature for their kind support of this competition.
 |
 |
This article now forms part of our coverage of the cutting-edge research done at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
