
What is proof? Philosophers have argued for centuries about the answer to this question, and how (and if!) things can be proven; no doubt they will continue to do so! Mathematicians, on the other hand, have been using "working definitions" of proof to advance mathematical knowledge for equally long.
Starting in this issue, PASS Maths is pleased to present a series of articles introducing some of the basic ideas behind proof and logical reasoning and showing their importance in mathematics.
In this article, we shall present a brief introduction to deductive reasoning, and take a look at one of the earliest known examples of mathematical proof.
Deductive reasoning
Given a set of facts that are known or assumed to be true, deductive reasoning is a powerful way of extending that set of facts. In deductive reasoning, we argue that if certain premises (P) are known or assumed, a conclusion (C) necessarily follows from these. For example, given the following (rather famous!) premises
P: Socrates is a man.
then the conclusion
follows via deductive reasoning. In this case, the deductive step is based on the logical principle that if A implies B, and A is true, then B is true, a principle that mediaeval logicians called modus ponens.
Of course, deductive reasoning is not infallible: the premises may not be true, or the line of reasoning itself may be wrong! This is how you can sometimes "prove" something that isn't actually true. There are any number of ways of "proving" that 1 = 2, for example. Here's an old favourite:
| \begin{array} {\bf } {\bf Let } $a$ = $b$ \\ {\bf Thus,}\\ $a^2 = ab$\\ $a^2 + a^2 = a^2 + ab$\\ $2a^2 = a^2 + ab$\\ $2a^2 - 2ab = a^2 + ab - 2ab$\\ $2a^2 - 2ab = a^2 - ab$\\ \\ {\bf Rewrite this as:}\\ $2(a^2 - ab) = 1(a^2 - ab)$\\ {\bf Dividing both sides by} $a^2 - ab$, {\bf we thus have:}\\ $2 = 1$\\ \\ {\bf QED.} \end{array} |
Can you spot the flaw in the argument?
Now, if a conclusion doesn't follow from its premises, the argument is said to be invalid and no reliable judgement can be made about whether the conclusion is true, regardless of whether or not the premises are true.
If the argument is valid but the premises are not true, then again the conclusion may or may not be true, but the argument can't help us decide this.
Finally, if the argument is valid and the premises are true, then the argument is described as sound, and we deem the conclusion to be true. From a pragmatic point of view, we can be said to have proved something if we can find a sound argument for it.
Table 1 summarises these different kinds of deductive arguments, and table 2 provides an example of each.
|
|
|
|
|
|
|
|
|
|
|
|
Table 1: Different kinds of deductive arguments.
|
P: Fish are mammals. P: Fish are warm-blooded. |
P: Mammals are cold-blooded. P: Humans are mammals. |
|
P: Fish are cold-blooded. P: Humans are not fish. |
P: Humans are warm-blooded. P: Fishermen are human. |
Table 2: Some example deductive arguments.
As the two invalid arguments in table 2 suggest, the conclusion of an invalid argument doesn't necessarily have to be false - it's just unproven by that particular argument!
In the beginning: Euclid's geometry
Euclid was born about 365 BC in Alexandria, Egypt, and died about 300 BC. Little is known of his life other than that he taught mathematics in Alexandria.
Euclid wrote a number of treatises, but the most famous is his Elements, a work on geometry that has been used as a textbook for over 2000 years! Rather than representing Euclid's original work, the Elements are now thought to be a summary of the geometrical knowledge current during his time. However, they represent one of the earliest uses of proof in the history of mathematics.
In his Elements, Euclid begins with a list of twenty-three definitions describing things like points, lines, plane surfaces, circles, obtuse and acute angles and so on (here, these are given in the appendix).
Euclid's definitions are neither true nor false: they simply act as a kind of dictionary, explaining what is meant by the various terms he will be using.
He then presents a set of ten assumptions. Five of these are not specific to geometry, and he calls them common notions:
- 1. Things which are equal to the same thing are also equal to one another.
- 2. If equals be added to equals, the wholes are equal.
- 3. If equals be subtracted from equals, the remainders are equal.
- 4. Things which coincide with one another are equal to one another.
- 5. The whole is greater than the part.
The other five assumptions are specifically geometric, and he calls them postulates :
- 1. It is possible to draw a straight line from any point to any point.
- 2. It is possible to produce a finite straight line continuously in a straight line.
- 3. It is possible to describe a circle with any centre and distance.
- 4. All right angles are equal to one another.
- 5. If a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
(Note that Playfair's Axiom (originally due to Proclus) that "through a point not on a given line, there passes not more than one parallel to the line" is a rather neater way of expressing postulate 5! In addition, in the nineteenth century, Legendre went on to show that postulate 5 is equivalent to the postulate that "the sum of the angles of a triangle is equal to two right angles").
Together, these common notions and postulates represent the axioms of Euclid's geometry. An axiom is a logical principle which is assumed to be true rather than proven, and which can be used as a premise in a deductive argument.
Euclid's set of axioms, or axiomatic system, represents a collection of "first principles" from which other principles can be produced using deductive reasoning. Of course, any deductive arguments are only sound if Euclid's common notions and postulates really are true!
An example proposition and proof
Euclid goes on in his Elements to present various geometric propositions, and shows them to be true using deductive inference within his axiomatic system.
An example is proposition 6: "If in a triangle two angles be equal to one another, the sides which subtend the equal angles will also be equal to one another."
Euclid's actual proof of this proposition is as follows:
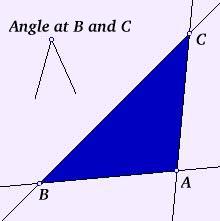
Figure 1: Euclid's proposition 6.
"Let ABC be a triangle having the angle ABC equal to the angle ACB;
I say the side AB is also equal to the side AC. For, if AB is unequal to AC, one of them is greater. Let AB be greater; and from AB the greater, let DB be cut off equal to AC the less; let DC be joined.
Then, since DB is equal to AC, and BC is common, the two sides DB, BC are equal to the two sides AC, CB respectively, and the angle DBC is equal to the angle ACB.
Therefore, the base DC is equal to the base AB, and the triangle DBC will be equal to the triangle ACB, the less to the greater, which is absurd. Therefore AB is not unequal to AC; it is therefore equal to it."
If you have a Java capable browser you can try a dynamic version of this drawing here.
Are Euclid's postulates true?
Both the Greeks of Euclid's time, and later Arabic mathematicians, had an intuition that the fifth postulate could actually be proven using the definitions and common notions and the first four postulates.
Many attempts to prove the fifth postulate in this manner were made, and often a putative proof would be accepted for a long period before being shown to be flawed. Typically, the flawed proofs contained a "circular argument": in one way or another, they assumed that what they were trying to prove (the fifth postulate) was true in order to prove it!
In fact, the fifth postulate is not derivable from the other postulates and notions, and nor is it universally true. Mathematicians continued to be fascinated by the fifth postulate throughout the centuries, but it was not until the nineteenth and twentieth centuries (through the efforts of a number of famous mathematicians including Legendre, Gauss, Bolyai, Lobachevsky, Riemann, Beltrami and Klein), that we came to know about geometries (called non-Euclidian geometries) where the fifth postulate is not true.
The fifth postulate can be shown to be true in a plane (or Euclidian) geometry. However, there are many other geometries where it is not true. Surprisingly enough, this is easy to illustrate! Consider the simple case of a sphere's surface.
It is impossible to draw a true straight line on a sphere without leaving the surface, So in spherical geometry the Euclidean idea of a line becomes a great circle. Thinking of the Earth, any line of longitude is a great circle - as is the equator. In fact the shortest path between any two points on a sphere is a great circle. (More generally, a minimal path on any surface is known as a geodesic.)
One of the consequences of Euclid's first four postulates is that if two different lines cross, they meet at a single point. This presents a small problem on the sphere, since distinct great circles always cross at two antipodal points! Two lines of longitude always cross at both the North and the South Pole!
But remember, we haven't yet said what the spherical analogue of a Euclidean point is! All we have to do is define a point in spherical geometry to be a pair of antipodal points and the problem promptly disappears.
According to Euclid's definition number 23, "Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction".
Given these definitions, it is easy to see that Euclid's first four postulates still make good sense. The fifth postulate, however, fails because it is impossible to draw two different lines that do not meet. In spherical geometry there are no parallel lines!
One of the consequences of the failure of the 5th postulate is that it is no longer true that the sum of the angles of a triangle is always 180 degrees.
In fact, there's a famous lateral-thinking puzzle that depends implicitly on this non-Euclidian geometry:
A hunter leaves his house one morning and walks one mile due south. He then walks one mile due west and shoots a bear, before walking a mile due north back to his house.
What colour is the bear?Euclid and deductive reasoning
The story of Euclidian geometry, and the subsequent discovery of non-Euclidian geometries, show the benefits and disadvantages of using deductive reasoning from axioms as a proof system.
Using his definitions, common notions and postulates as an axiomatic system, Euclid was able to produce deductive proofs of a number of important geometric propositions. His axioms and proofs have been a useful set of tools for many subsequent generations of mathematicians, and show how powerful and beneficial deductive reasoning can be!
However, the long and painful process of discovering non-Euclidian geometries has shown one of the limitations of deductive reasoning in an axiomatic system: that any proof is only as good as the axioms it starts off with! In the Euclidian plane, Euclid's fifth postulate is true, and his valid proofs are sound. In non-Euclidian geometries such as the surface of a sphere, however, the fifth postulate is not true, and Euclid's proofs are therefore unsound.
Bibliography
- There are plenty of good introductory texts about logic and reasoning. "Thinking Things Through" by Clark Glymour (MIT Press, 1997) is a good place to start, and Critical Thinking by Francis W. Dauer (OUP, 1989) is a more comprehensive guide.
- The University of Toronto Mathematics Network has some nicely-annotated Classic Fallacies, including a detailed look at our initial example.
- There is an interactive html version of Euclid's Elements at Clark University.
About the author

Image © Kerry Rodden 1998
Appendix - Euclid's Definitions
- 1. A point is that which has no part.
- 2. A line is breadthless length.
- 3. The extremities of a line are points.
- 4. A straight line is a line which lies evenly with the points on itself.
- 5. A surface is that which has length and breadth only.
- 6. The extremities of a surface are lines.
- 7. A plane surface is a surface which lies evenly with the straight lines on itself.
- 8. A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
- 9. And when the lines containing the angle are straight, the angle is called rectilineal.
- 10. When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.
- 11. An obtuse angle is an angle greater than a right angle.
- 12. An acute angle is an angle less than a right angle.
- 13. A boundary is that which is an extremity of anything.
- 14. A figure is that which is contained by any boundary or boundaries.
- 15. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another;
- 16. And the point is called the centre of the circle.
- 17. A diameter of the circle is any straight line drawn through the centre and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.
- 18. A semicircle is the figure contained by the diameter and the circumference cut off by it. And the centre of the semicircle is the same as that of the circle.
- 19. Rectilineal figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
- 20. Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.
- 21. Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute.
- 22. Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia.
- 23. Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.