
Euclidean Geometry
The famous mathematician Euclid is credited with being the first person to axiomatise the geometry of the world we live in - that is, to describe the geometric rules which govern it. Based on these axioms, he proved theorems - some of the earliest uses of proof in the history of mathematics. Euclid's work is discussed in detail in The Origins of Proof, from Issue 7 of Plus.
Euclid's famous treatise, the Elements, was most probably a summary of what was known about geometry in his time, rather than being his original work. In it, he sets out five geometric "postulates", the fifth of which is this:
If a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.In the nineteenth century, this postulate was shown by Legendre to be equivalent to the statement that
The sum of the angles of a triangle is equal to two right angles.
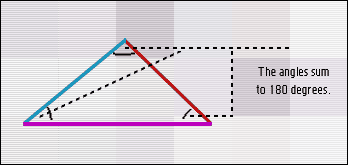
The angles of a triangle sum to 180 degrees.
The fifth postulate, as Euclid stated it, seemed sufficiently complicated that it should be provable from the other postulates, rather than something to be taken as given. In the two thousand years following Euclid, many mathematicians, professional and amateur, tried to prove that the fifth postulate followed from the first four - and failed.
Geometry in which the fifth postulate is assumed is known as "Euclidean" or "flat" geometry. Its defining characteristic is that the angles of a triangle always sum to 180 degrees.
The famous artist Escher was fascinated by geometry. In the picture below, he illustrates a flat geometry with interlocking angels and devils.
![[IMAGE: Regular division of the plane]](/issue18/xfile/flat.jpg)
M.C. Escher's "Regular division of the plane".
All M.C. Escher works © 2002 Cordon Art - Baarn - Holland (www.mcescher.com).
All rights reserved. Used by permission.
Eventually, in the nineteenth century, an example of a geometry was found in which the fifth postulate did not hold, although the other four did. Surprisingly for something that took so long, one example is quite easy to visualise. It is the geometry of the surface of a sphere, known as "spherical geometry".
Spherical Geometry
In spherical geometry the Euclidean idea of a line becomes a great circle, that is, a circle of maximum radius. It is no longer true that the sum of the angles of a triangle is always 180 degrees. Very small triangles will have angles summing to only a little more than 180 degrees (because, from the perspective of a very small triangle, the surface of a sphere is nearly flat). Bigger triangles will have angles summing to very much more than 180 degrees.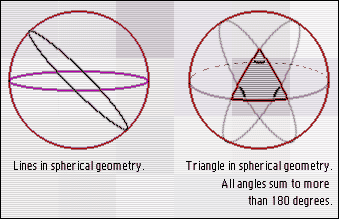
The angles of a triangle sum to more than 180 degrees.
One funny thing about the length of time it took to discover spherical geometry is that it is the geometry that holds on the surface of the earth! But we never really notice, because we are so small compared to the size of the earth that if we draw a triangle on the ground, and measure its angles, the amount by which the sum of the angles exceeds 180 degrees is so tiny that we can't detect it.
Here is Escher's depiction of spherical geometry, again using the angel/devil motifs.
![[IMAGE: Sphere with Angels and Devils]](/issue18/xfile/sperical.jpg)
M.C. Escher's "Sphere with Angels and Devils".
All M.C. Escher works © 2002 Cordon Art - Baarn - Holland (www.mcescher.com).
All rights reserved. Used by permission.
Now you might ask, is there a geometry in which Euclid's fifth postulate fails, but in the opposite way? That is, is there a geometry in which the angles of a triangle sum to less than 180 degrees?
The answer is that there is. It is known as hyperbolic geometry.
Hyperbolic Geometry
Hyperbolic geometry isn't so easy to visualise as spherical geometry is, because it can't be modelled in three-dimensional Euclidean space without distortion. In hyperbolic geometry, as in spherical geometry, Euclid's first four postulates hold, but the fifth does not. We assume that there exists a line and a point not on the line with at least two parallels to the given line passing through the given point.One way of visualising hyperbolic geometry is called the Poincaré half-plane model. The relationship between this model and "real" hyperbolic space is similar to that between flat maps and our spherical world. For example, if you fly a plane in a straight line from London to San Francisco, and then draw your route on a map, the route won't look straight any more, because maps distort straight lines. (In the standard "Mercator projection" maps, distances near the Poles are greatly distorted.) In the Poincaré half-plane model, the hyperbolic plane is flattened into a Euclidean half-plane. As part of the flattening, many of the lines in the hyperbolic plane appear curved in the model. Lines in the hyperbolic plane will appear either as lines perpendicular to the edge of the half-plane or as circles whose centres lie on the edge of the half-plane.
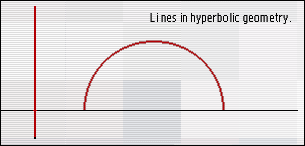
Lines in hyperbolic geometry.
As you get nearer and nearer to the edge of the halfplane, distances get greater and greater, so that you can only approach the edge, but never arrive. A triangle is then the intersection of three "lines", and if you experiment a little, you should be able to convince yourself that the angles of a hyperbolic triangle always add up to strictly less than 180 degrees.
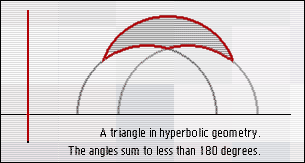
The angles of a triangle sum to less than 180 degrees.
There are other ways to model hyperbolic geometry on the flat plane. One is to represent the hyperbolic plane on a circle, with distances getting greater and greater as you approach the circumference. A third Escher angel/devil picture illustrates this beautifully.
![[IMAGE: Circle limit IV]](/issue18/xfile/hyperbolic.jpg)
M.C. Escher's "Circle limit IV".
All M.C. Escher works © 2002 Cordon Art - Baarn - Holland (www.mcescher.com).
All rights reserved. Used by permission.
Both spherical and hyperbolic geometries are examples of curved geometries, unlike Euclidean geometry, which is flat. In spherical geometry, the curvature is positive, in hyperbolic geometry, it is negative.
Curved space?
A question that has interested cosmologists for quite some time now is whether the universe we live in is flat, in this sense that the angles of a triangle always add up to 180 degrees. It certainly seems to be, but as we know from history, this isn't necessarily a good guide! Einstein's theory of relativity tells us that gravity causes space to curve locally. Around massive objects, like stars, space is distorted. This can be seen by the way beams of light are bent as they pass near to such objects. Near black holes, the distortion is so strong that beams of light that go too close are "sucked in" to the black hole, never to reemerge. So if you imagine drawing triangles with beams of light as your sides, there will be no guarantee that the angles will sum to 180o, unless you have chosen your location carefully, far away from massive objects!But there is another way in which the universe might not be flat, and that is on the very large scale. As we see further and further away, using ever more powerful telescopes, we could eventually realise that the whole of space is slightly curved, so slightly that it was not apparent except on enormous scales.
Elsewhere in this issue of Plus, (see No place like home), Sir Martin Rees discusses this very question. He tells us that the current view, using very recent data, is that in fact we do live in a flat universe, or if there is a curvature, it is very slight.
About the author
Helen Joyce is an assistant editor of Plus.