Bisecting a given angle using only a pair of compasses and a straight edge is easy. But trisecting it - dividing it into three equal angles - is in most cases impossible. Why?

Bisecting an angle

If we have a pair of lines meeting at a point O, and we want to bisect the angle between them, here's how we do it.

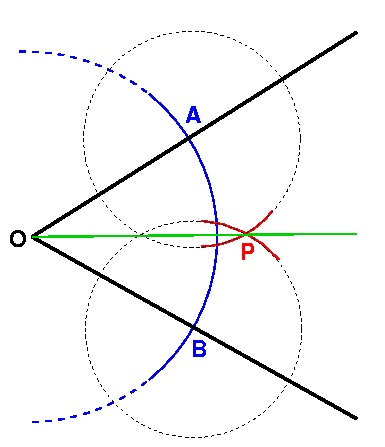
Bisecting angle AOB using straight edge and compasses.

Put the point of the compass at O and draw a circle (of any radius you like). This is the blue arc in the diagram. The circle will cross the two lines at two points: call these A and B.

Now put the point of the compass at A and draw an arc of a circle, as shown in the diagram. Without changing the radius at which the compass is set, move its point to B and draw another arc of a circle. These are the red arcs in the diagram. The point where the two arcs cross, P, can then be joined to O using the straight edge (the green line), and angle POB is half of angle AOB. If the arcs don't cross, then of course you need to use larger circles!

Trisecting an angle

What about trisecting an angle? Why is it so difficult? There are a few special cases of angles for which it can be done - for example, pi/2 radians (90 degrees). For the general case, however, the Greeks couldn't work out how to do it, despite expending vast amounts of energy on the problem.

Trisecting an arbitrary angle can be done if you cheat by using a measuring ruler instead of a plain straight edge (you can find out how in the sci.math FAQ file), or even if you simply draw two little marks on your straight edge. However, to "play by the rules" you aren't allowed any marks on the straight edge at all - it must be completely blank.

The problem of whether trisection could be done in the general case remained a mathematical mystery for millennia - it was only in 1837 that it was eventually proved to be impossible by Pierre Wantzel, a French mathematician and expert on arithmetic. This was a great achievement for a man of 23, who subsequently died at the tragically young age of 33.

So why is it impossible? Pierre showed that the two problems of trisecting an angle and of solving a cubic equation are equivalent. Moreover, he showed that only a very few cubic equations can be solved using the straight-edge-and-compass method - most cannot. He thus deduced that most angles cannot be trisected.

Footnote : The real mystery

Despite the fact that Wantzel's proof means that we now know that it's impossible to trisect a general angle, people keep trying. The mathematics department where PASS Maths is based receives quite serious letters every so often from individuals who think they've cracked the problem, offering famous people in the department the opportunity to "buy" the "proof" (sometimes for large amounts of money!). One such letter even missed out several pages of the "proof" on the grounds of security of the writer's copyright!

Needless to say, all these so-called proofs contain flaws and are worthless. If the writers really wanted to convince anyone that it is possible to trisect the angle, their time would be better spent trying to find an error in Wantzel's proof. The real mystery here is why people keep trying to solve the problem in the face of a proof of its impossibility. How would you reply to them?