
One of the buzz words in the sciences of complexity is emergence. As you build up a complex situation step by step, it appears that thresholds of complexity can be reached which herald the appearance of new structures and new types of behaviour which were not present in the building blocks of the complexity. The World-Wide Web, or the stock market, or human consciousness, seem to be phenomena of this sort. They exhibit collective behaviour which is more than the sum of their parts. If you reduce them to their elementary components, then the essence of the complex behaviour disappears. Such phenomena are common in physics too. A collective property of a liquid, like viscosity, which describes its resistance to flowing, emerges when a large number of molecules combine. It is real but you won't find a little bit of viscosity on each atom of hydrogen and oxygen in your cup of tea.

The World Wide Web
Emergence is itself a complex, and occasionally controversial, subject. Philosophers and scientists attempt to define and distinguish between different types of emergence, while a few even dispute whether it really exists. One of the problems is that the most interesting scientific examples, like consciousness or life, are not understood and so there is an unfortunate extra layer of uncertainty attached to these iconic examples. Here, mathematics can help. It gives rise to many interesting emergent structures which are well defined and which suggest ways in which to generalise them into whole families of related examples.
Take finite collections of positive integers like [1,2,3,6,7,9]. Then, no matter how large they are, they will not possess the properties that emerge when a collection of integers becomes infinite. As Georg Cantor first showed clearly in the 19th century, infinite collections of numbers possess properties not shared by any finite subset of them, no matter how large it may be. Infinity is not just a big number. Add one to it and it stays the same; subtract infinity from it and it can stay the same. The whole is not only bigger than its parts, it also possesses emergent features that are qualitatively different to those of its parts.
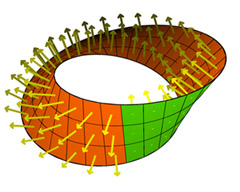
Even though the individual squares that make up the surface of the Möbius strip are two-sided, when they are joined together and twisted, the surface as a whole only has one side.
Many other examples can be found in topology, where the global structure of a space can be strikingly different to its local structure. The most familiar is the Möbius strip. We make one by taking a rectangular strip of paper and gluing the ends together after adding a single twist to the paper. It is possible to make up that strip of paper by sticking together small squares of paper in a patchwork. The Möbius strip then begins to look like a type of emergent structure. All the squares that were put together to make the strip had two sides. But when the ends are twisted and stuck together to form the whole Möbius strip, it has only one side. Again, the whole has an "emergent" property that is not shared by any of its component parts. It emerges only as a consequence of how those parts are organised.
Perhaps you can think of some other examples of emergent mathematics?