Which gives a tighter fit: a square peg in a round hole or a round peg in a square hole? (The tighter fit is the one for which the ratio of peg area to hole area is greater.)

Solution

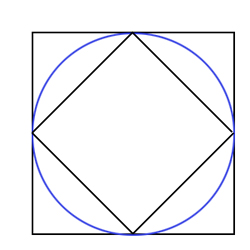
Consider the following picture:

Suppose that the side length of the large square is so its area is Then the circle has radius so its area is By Pythagoras’ theorem the small square has side length so it’s got area

The square peg in round hole fit is given by the ratio of the area of the small square to the area of the circle, which is

The round peg in square hole fit is given by the ratio of the area of the circle to the area of the large square, which is

Since we have so Dividing by 4 gives so the round peg in a square hole gives the better fit.

Back to original puzzle

This puzzle was contributed by Colm Mulcahy, Associate Professor of Mathematics at Spelman College in Atlanta, Georgia. Colm's own puzzles have appeared in Math Horizons and in the New York Times. He is a long-time columnist for the Mathematical Association of America and has his own blog. You can follow Colm on Twitter.