Add new comment

Triples and quadruples: from Pythagoras to Fermat

Pythagoras' theorem. Image: Wapkaplet.

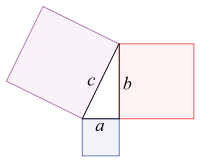
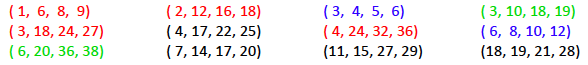If there’s one bit of maths you remember from school it’s probably Pythagoras’ theorem. For a right-angled triangle with sides $a$ , $b$ , $c$ , where $c$ is the side opposite the right angle, we have

$a^2+b^2=c^2.$

If three positive whole numbers $a$ , $b$ and $c$ satisfy this equation — if they form the sides of a right-angled triangle — they are said to form a Pythagorean triple.

One question that intrigued Pythagoras himself, as well as other ancient Greek mathematicians, is how to generate Pythagorean triples. If I give you a positive number $a$ , can you find two numbers $b$ and $c$ so that $a$ , $b$ and $c$ form a Pythagorean triple? In this article we’ll explore this question, and we’ll also see how the idea extends to sets of four numbers, called Pythagorean quadruples.

Pythagorean triples

First of all, here are some examples of Pythagorean triples:

Some Pythagorean triples.

The triples written in red are multiples of each other and so are the triples written in blue: you get $(6, 8, 10),$ $(9,12,15)$ and $(12, 16, 20)$ by multiplying the components of $(3, 4, 5)$ by 2, 3 and 4 respectively, and you get $(10, 24, 26)$ by multiplying the components of $(5, 12, 13)$ by 2.

In general, if $k$ is a positive whole number and $(a,b,c)$ is a Pythagorean triple, then so is $(ka, kb, kc)$ , since

$(ka)^2+(kb)^2 = k^2a^2+k^2b^2 = k^2(a^2+b^2)=k^2c^2=(kc)^2.$

Geometrically, if one Pythagorean triple is a multiple of another, then the corresponding triangles are similar.

Pythagoras as depicted by Raffaello Sanzio in his painting The school of Athens.

If a Pythagorean triple isn’t a multiple of another Pythagorean triple, then we say that it is a primitive triple. You can recognise a primitive Pythagorean triple by the fact that the numbers $a$ and $b$ do not have a common divisor. In our example $(3, 4, 5)$ is a primitive Pythagorean triple while $(6, 8, 10),$ $(9, 12, 15)$ and $(12, 16, 20)$ are not. Similarly $(5, 12, 13)$ is a primitive triple whereas $(10, 24, 26)$ is not.

If you're given a Pythagorean triple it's easy to generate new non-primitive ones simply by taking its multiples. But given just a number, can you find a Pythagorean triple with that number as one of its components? One method for doing this has been attributed to Pythagoras himself. First note that if

$a^2+b^2=c^2$

then

$c^2-b^2=a^2.$

Now consider the two expressions

$(a^2+1)^2 = a^4+2a^2+1$

and

$(a^2-1)^2 = a^4-2a^2+1.$

They differ by exactly $4a^2,$ so the two expressions

$\frac{(a^2+1)^2}{4}$

and

$\frac{(a^2-1)^2}{4}$

differ by $a^2.$

Plato (left) with Aristotle (right) as depicted by Raffaello Sanzio in his painting The school of Athens.

Therefore, if we choose

$b=\sqrt{\frac{(a^2-1)^2}{4}}=\frac{(a^2-1)}{2}$

and

$c=\sqrt{\frac{(a^2+1)^2}{4}}=\frac{(a^2+1)}{2}$

we have

$a^2+b^2 = a^2 + \frac{(a^2-1)^2}{4} = \frac{(a^2+1)^2}{4} = c^2.$

For the numbers $a$ , $b$ and $c$ to represent a Pythagorean triple we need

$b =\frac{(a^2-1)}{2}$

and

$c = \frac{(a^2+1)}{2}$

to be whole numbers. This means that both

$a^2-1$

and

$a^2+1$

need to be even, which in turn implies that $a^2$ needs to be odd. But the square of a number is odd only if the number itself is odd, so this method only works for odd $a$ .

There is however an easy way to derive a formula for even values from the above. If $a$ , $b$ and $c$ form a Pythagorean triple of the form described above, then so do

$a_1=2a,$

$b_1=2b=a^2-1=\left(\frac{a_1}{2}\right)^2-1$

$c_1=2c=a^2+1=\left(\frac{a_1}{2}\right)^2+1.$

This method for generating triples from even numbers $a_1$ has been attributed to Plato. Here is a list of Pythagorean triples generated from both even and odd numbers using these two methods:

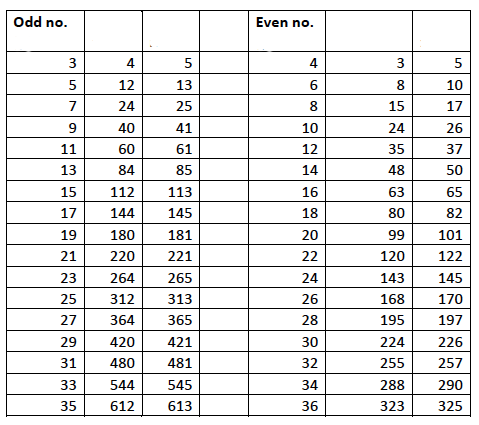
Since the methods give us a triple for every positive whole number we see that there are infinitely many Pythagorean triples. But can these methods generate all of them? The answer is no. For example, the triple $(20, 21, 29)$ is absent from the list above. A general formula was described by Euclid in his famous book The Elements. Take any two positive whole numbers $m$ and $n$ with $m>n$ . Similarly to our reasoning above, notice that

$(m^2-n^2)^2 = m^4-2m^2n^2 +n^4$

and

$(m^2+n^2)^2 = m^4+2m^2n^2 +n^4$

differ by $4m^2n^2.$ So setting

$a = m^2-n^2$

$b=\sqrt{4m^2n^2} = 2mn$

$c=m^2+n^2$

gives

$a^2+b^2=c^2.$

Since $m$ and $n$ are positive whole numbers and $m>n$ all three numbers $a$ , $b$ and $c$ are also positive whole numbers, so we have a Pythagorean triple. Every primitive Pythagorean triple can be generated from a unique pair of numbers $m$ and $n$ , one of which is even. And once you have the primitive ones you can generate all Pythagorean triples simply by multiplying. So Euclid’s formula really does give you all the triples there are.

Pythagorean quadruples

Now let’s look at Pythagorean quadruples which consist of four positive whole numbers instead of three. In a Pythagorean quadruple the sum of squares of first three numbers gives us the square of the fourth:

$a^2+b^2+c^2=d^2.$

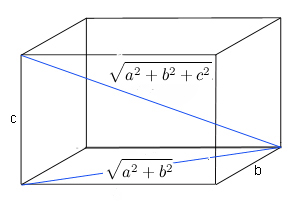
Geometrically we can think of a Pythagorean quadruples in terms of a rectangular box with sides $a$ , $b$ and $c$ . The length of the diagonal of this box is

$\sqrt{a^2+b^2+c^2}.$

Hence the sides together with the diagonal form a Pythagorean quadruple. This is why Pythagorean quadruples are also called Pythagorean boxes. As before, if $(a,b,c,d)$ is a Pythagorean quadruple, then so is $(ka,kb,kc,kd)$ for any positive whole number $k$ . If the greatest common divisor of $a$ , $b$ and $c$ is 1 then the quadruple is called primitive. Here are some examples of Pythagorean quadruples with members that are multiples of each other in the same colour (red, blue or green):

Some Pythagorean quadruples.

We can generate a Pythagorean quadruple from any two numbers $m$ and $n$ simply by noting that

$(m+n)^2=m^2+2mn+n^2.$

Thus, setting

$a = m^2, b = 2mn, c= n^2$ and $d=(m+n)^2$ gives us a Pythagorean quadruple.

This also gives us a way of generating a Pythagorean quadruple from a single even number $p$ . Firstly, note that if $p$ is even, then $p^2$ is even. Now find two numbers $m$ and $n$ so that $m n = p^2/2.$ Set

$a=m$

$b=p=\sqrt{2mn}$

$c=n$

and

$d=(m+n)^2.$

Then

$a^2+b^2+c^2 = m^2+ 2mn + n^2 = (m+n)^2 = d^2$

gives us our Pythagorean quadruple. For example, if $p=2$ , then $p^2/2=2$ so choose $m=1$ and $n=2.$ We get the quadruple $(1, 2, 2, 3)$ with

$1^2+2^2+2^2 = 1+4+4=9=3^2.$

For $p=4$ we have $p^2/2=8.$ We now have two choices as $8=2 \times 4$ and $8=1 \times 8.$ The first choice gives the quadruple $(2, 4, 4, 6)$ with

$2^2+4^2+4^2 = 4+16+16 = 36 = 6^2.$

The second choice gives the quadruple $(1, 4, 8, 9)$ with

$1^2 + 4^2+8^2 = 1 + 16 + 64 = 81 = 9^2.$

You can continue to generate quadruples from even numbers $p$ in this way.

Can we generate all Pythagorean quadruples?

Not all Pythagorean quadruples are of the form

$(m+n)^2=m^2+2mn+n^2,$

so not all of them can be generated using the method we just described — we need to be a little cleverer. Suppose that you’re given two numbers $a$ and $b.$ Now find a number $p$ which divides $a^2+b^2$ but so that $p^2 < a^2+b^2.$ If $a$ and $b$ are both even, then we also require that $p$ itself is even.

Euclid (the man with the compass) as depicted by Raffaello Sanzio in his painting The school of Athens.

Now let

$c= \frac{a^2+b^2-p^2}{2p}.$

Then

$\displaystyle a^2+b^2+c^2$	$\displaystyle =$	$\displaystyle a^2+b^2+\frac{(a^2+b^2)^2-2(a^2+b^2)p^2+p^4}{4p^2}$
$\displaystyle$	$\displaystyle =$	$\displaystyle a^2+b^2 +\frac{(a^2+b^2)^2}{4p^2}-\frac{(a^2+b^2)}{2}+\frac{p^2}{4}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \frac{(a^2+b^2)^2}{4p^2}+\frac{(a^2+b^2)}{2}+\frac{p^2}{4}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \left(\frac{(a^2+b^2+p^2)}{2p}\right)^2.$

So letting

$d = \frac{(a^2+b^2+p^2)}{2p}$

we have

$a^2+b^2+c^2=d^2.$

But are $a$ , $b$ , $c$ and $c$ positive whole numbers? This is why we’ve imposed conditions on $p.$ You can show that as long as $a$ and $b$ are either both even, or if one is even and one is odd, then the conditions ensure that $a$ , $b$ , $c$ and $d$ are positive whole numbers.

(Click here to see why.)

If $a$ and $b$ are both odd it is impossible to generate a Pythagorean quadruple from them by this method.

But the important point is that you can construct every primitive Pythagorean quadruple from two numbers $a$ and $b$ in the way we’ve just shown. And again, once you have the primitive ones, you can get all the others just by multiplying.

Generating a series of squares

Another nice thing to notice is that using our mechanism for generating triples, we can make sums of squares of any length. Let’s start with the triple $(3,4,5).$ We can generate another triple starting with the number 5: it’s $(5,12, 13).$ Thus we have

$3^2 + 4^2 = 5^2$

and

$5^2 + 12^2 = 13^2.$

Rearranging the second equation gives

$5^2 = 13^2-12^2.$

Substituting this into the first equation and rearranging gives

$3^2+4^2+12^2=13^2,$

so we have the quadruple $(3,4,12,13).$ Proceeding in a similar way, always using the biggest of the current set of numbers to generate a new triple, we can construct the quintuple $(3, 4, 12, 84, 85)$ and the sextuple $(3, 4, 12, 84, 3612, 3613)$ and so on, ad infinitum.

Cubes and beyond

Pythagorean quadruples consist of a sum of squares, but what if we look at sums of cubes of the form

$a^3+b^3+c^3=d^3.$

These are called cubic quadruples. Here are a few examples (again, quadruples written in red, blue or green are multiples of each other).

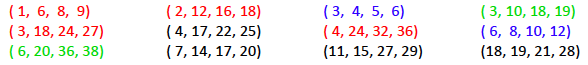
Some cubic quadruples.

We won’t explore how to generate them here, but instead ask a question that turns out to be more interesting: are there also cubic triples? This question is the subject of one of the most famous results in mathematics: Fermat’s last theorem. The theorem says that there are no three positive whole numbers $a$ , $b$ and $c$ such that

$a^3+b^3=c^3.$

In fact, the theorem says more than that: for any positive whole number $n$ greater than two it is impossible to find three positive whole numbers $a$ , $b$ and $c$ such that

$a^ n+b^ n=c^ n.$

The result was made famous by the French mathematician Pierre de Fermat in 1637. Fermat wrote in the margin of his book that he had "discovered a truly marvelous proof of this, which this margin is too narrow to contain". For over 300 years mathematicians desperately tried to reconstruct this marvellous proof, but they didn't succeed. It was not until 1995 that the mathematician Andrew Wiles proved the result, using sophisticated mathematics Fermat could not possibly have known about.

About the author

Chandrahas Halai is a mathematics enthusiast from the land of the Shulba sutras, the Bakhshali manuscript, and mathematicians like Aryabhatt, Brahmagupta, Bhaskaracharya, Ramanujan and many more. He is a consultant in the field of computer aided engineering, engineering optimisation, computer science and operations research. He writes research papers, articles and books on mathematics, physics, engineering, computer science and operations research. In his spare time he likes doing nature photography and painting.

Plus.Maths.org