The Sun, the Moon and trigonometry
How much further away is the Sun than the Moon? How much bigger is the Sun than the Moon? And how are you supposed to work out the answers if you are an ancient Greek who doesn't even have a telescope?
If you are Aristarchus of Samos, who lived around 2300 years ago, then you'll rely on your excellent geometrical expertise combined with an important insight: that the Moon shines at night because it is illuminated by the Sun. On the face of it, this latter fact is far from obvious, but then Aristarchus was a pioneer. Unlike many, many astronomers who came after him, he recognised that the Earth moved around the Sun, rather than the other way around.
Armed with the knowledge that the Sun illuminates the Moon, Aristarchus realised that at half Moon, the triangle formed by the Earth (E), the Moon (M) and the Sun (S) has a right angle at M.
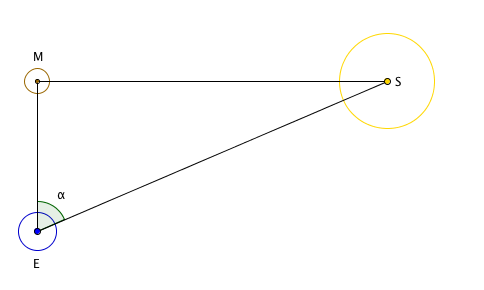
Diagram not to scale.
You can convince yourself of this by imagining the Sun in different places in the diagram above and checking that the parallel rays of light emanating from it illuminate exactly half of the Moon (as seen from Earth) only when there is a right angle at M.
Aristarchus was after the relative distance to the Sun and the Moon, that is, he was after the ratio 
, where 
is the distance from the Earth to the Sun and 
is the distance from the Earth to the Moon. If you know your trigonometry you know that
![\[ \frac{EM}{ES} = \cos {\alpha }, \]](/MI/32af15a24776bf257c6cce461bfa3fe9/images/img-0004.png) |
where 
is the angle at the corner 
of the triangle. Therefore
![\[ \frac{ES}{EM} = \frac{1}{\cos {\alpha }}. \]](/MI/32af15a24776bf257c6cce461bfa3fe9/images/img-0007.png) |
Taking the estimate 
gives the answer
![\[ \frac{ES}{EM} = \frac{1}{\cos {89.85^\circ }} \approx 382. \]](/MI/32af15a24776bf257c6cce461bfa3fe9/images/img-0009.png) |
So the Sun is just short of 400 times further from Earth than the Moon. Aristarchus also noticed that during a solar eclipse the Moon completely covers the Sun. This gives us the following diagram: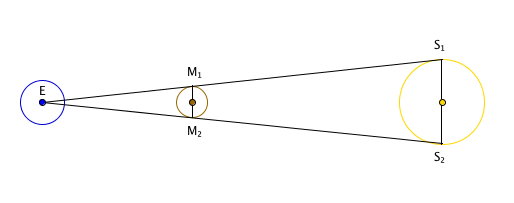
Diagram not to scale.
Using the fact that the ratio between 
and 
is the same as the ratio between 
and 
(because we are looking at two similar triangles) we can deduce that the Sun’s diameter is about 400 times bigger than the Moon’s diameter.
The result Aristarchus came up with was very different. He estimated the Sun to be between 18 and 20 times further away than the Moon. This is partly because he didn’t have the means to measure 
accurately enough and took it to be equal to 
Using this value in the calculation above gives that the Sun is about 19 times further away than the Moon: a small variation in an angle close to 
leads to a large variation in 
.
The reason why Aristarchus could only come up with the range from 18 to 20, rather than a single number, is that trigonometry hadn’t been developed yet. He didn’t have the notion of a cosine, let alone any tables in which to look up the cosine of a given angle. Instead, he had to use a more complicated geometric argument to come up with his approximate answer. Which illustrates why trigonometry is so useful for astronomers.
About the author
Marianne Freiberger is Editor of Plus.