

A different solution to noisy phone calls (Image by Christian Hessmann, CC BY 2.0)
When you next admire a stack of oranges, you'll agree with the greengrocer that it's useful to know how to pack round things so that you waste as little space as possible. But it is hard to imagine that packing round things, balls, in higher dimensions should have practical application. In fact, it is hard to imagine packing balls in higher dimensions at all. And yet, seemingly exotic mathematics such as this regularly finds important practical applications. In this case, to problems arising in digital communications. Before I explain the ideas involved, let me give a flavour of a typical question.
The problem we set to understand is how to efficiently transmit a signal or message in the presence of noise. For instance, we might be interested in transmitting human voice over the phone, data to a CD or information via the internet. Naturally, the signal should be transmitted with the least amount of errors and in the most cost-efficient manner possible.
Shannon's sampling theorem
Typically a signal – say, a human voice to be transmitted over the phone – varies continuously over time. A signal of this type is called analog. Analog signals suffer from some disadvantages, such as susceptibility to noise and often being very complex. For these practical reasons it is desirable to convert it to digital form, a form in which the signal takes only finitely many values and varies more simply. Such a conversion intuitively leads to a loss of information. However, real-life signals are band-limited, meaning that their range of frequencies is limited. For example, a human voice ordinarily does not exceed 8,000 hertz (cycles per second) and conventional orchestra music has no frequencies higher than 20,000 hertz. This allows them to be converted without any loss of information thanks to a theorem by Claude Shannon, the father of computer science and information theory. (You can read more about Shannon's work in these articles.)
To convert the signal to digital form we must sample it. Sampling means to record the level of the signal at various times. It is intuitively clear that the more frequently one samples the signal, the better the result. Surprisingly this is not strictly true. Shannon's sampling theorem states that given a band limited signal, there is a certain rate at which we can sample the signal and be able to completely recover the signal from these samples; any faster sampling produces no improvement. (In the presence of noise, however, it is wise to sample more because some of the samples might be misleading.)
To illustrate this discussion, consider the following signal, which is being sampled too slowly:
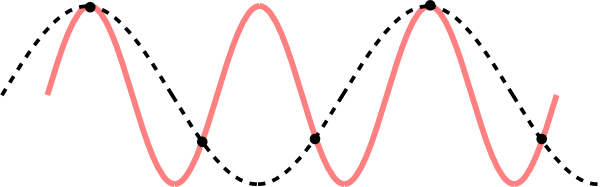
The red curve is the signal. The black dots correspond to samples. The dashed curve is another signal which would result in the same values for samples taken at the same points. This plot shows that the sampling frequency here is not sufficient because we cannot uniquely reconstruct the original signal.
As the figure shows, we cannot reconstruct the original signal from the samples because there are other signals that may have given rise to the same samples. However, if we had sampled faster, then the sampling theorem would guarantee that we could recover the signal uniquely.
In a higher dimension...
We can apply the sampling theorem to our problem of communication in the presence of noise. Imagine that we have a radio signal. We sample it, and these samples uniquely determine the signal. Hypothetically, suppose that the sampling occurs at each microsecond up to 1000 microseconds. At each of these times we measure the signal, assigning it a numerical value, thus obtaining 1000 numbers. Just as the location of a landmark on the globe can be specified using two coordinates (ie, latitude and longitude), so these 1000 numbers specify the signal. We can think of these 1000 numbers as coordinates and imagine the signal they describe to be a point in 1000-dimensional space. (You can read more about higher-dimensional spaces here.)
At this point one might wonder: why should we want to represent a signal in this weird fashion? The reason that Shannon did so was to prove an important theorem in the theory of communication concerning the effect of noise on signal transmission. (You can find the details in his 1949 paper.) His goal was to understand how to transmit the signal through a noisy channel (eg, speech recognition in the presence of noise) with a minimum amount of error.

Suppose I send you a signal, think of it as the point "Signal sent" in the image on the right. Then the presence of noise means that you will not necessarily receive this signal, this point in space. Rather you will potentially receive some other point ("Signal received") within a small ball (the "error ball"), centred on the signal sent, containing the signal received. (A ball in a higher-dimensional space is defined in exactly the same way as for three-dimensional space: as the set of points less than or equal to some set distance – the radius – from a central point.) The size of the error ball is determined by how noisy the channel is – the noisier the channel, the larger the ball and the possible error.
So how can we communicate if the signal sent is not necessarily the signal received? To do this we must agree ahead of time on a restricted vocabulary of signals. When we receive a signal, we pick the geometrically closest possible signal in the vocabulary.
Having received a signal ("Signal received"), we assume that it is actually within an error ball centred on some point in our agreed vocabulary of signals. The situation we don't want is one in which it is ambiguous where the signal came from, such as in the image below, on the left. Here the two error balls overlap, introducing the ambiguity. So we must choose the words of the vocabulary sufficiently far apart, as in the image below, on the right, so there is no ambiguity.
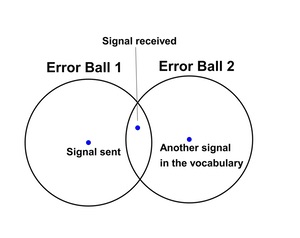
If the agreed vocabulary of signals are too close together, the error balls will intersect, leading to ambiguity.
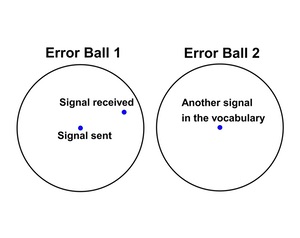
However if there is no overlap, then there is no ambiguity.
In order to have as large a vocabulary as possible, we clearly want to pack as many balls as possible into our space of signals. Therefore ball packing in higher dimensions tells us both how to efficiently code the signals we are interested in and also what the limit is on the size of our vocabulary. Just another example of how exotic maths can lead to important everyday applications.
About the author

Emmanuel Tsukerman is a PhD candidate in applied mathematics at UC Berkeley. Before starting his PhD, he completed his BS in mathematics and MSc in Computational and Mathematical Engineering at Stanford University.