
In this article we explore some of the symmetries that hide within the multiplication table of positive whole numbers.
Let us start with the standard multiplication table. The table below contains the numbers 1 to 10 in the first row and the first column. Any other square contains the product of the first number in its row and the first number in its column.
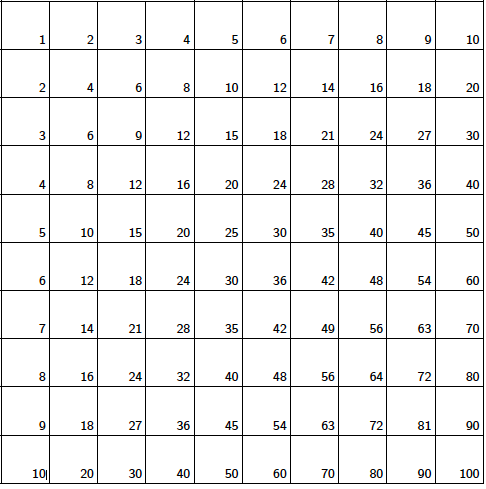
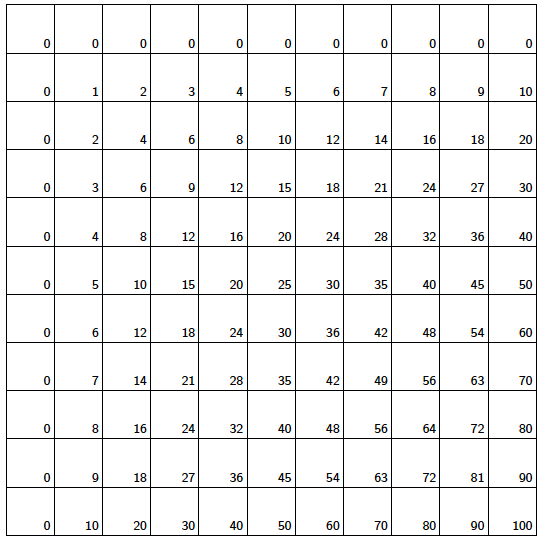
Single multiples
We begin with $k=2$: we assign the colour blue to every square in the multiplication table that is a multiple of $2$. (The number $0$ is a multiple of $2$, so all the $0$ squares are blue.)
Here we have extended the table a bit so that it runs until the number 15 in the horizontal direction. Indeed, since the complete multiplication table on positive integers is infinite on two sides, we will continue to tweak the dimensions of the tables in what follows to display the emerging patterns more clearly.
Note that the whole pattern above can be pieced together using the fundamental building block:
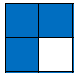

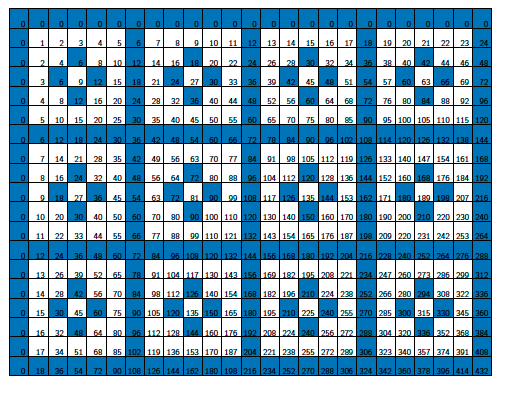
Multiple multiples of consecutive numbers
A more interesting pattern emerges if we use multiple multiples, and corresponding to them, multiple colours. In the following figure, the numbers that are multiples of $2$ are coloured red, and those that are multiples of $3$ are coloured orange (with the orange taking precedence over the red in the case of multiples of both $2$ and $3$, that is, multiples of $6$).This gives the following pattern.


We can carry on playing this game indefinitely. The next four figures use multiples of four, five, six and seven consecutive numbers respectively, and four, five, six and seven colours respectively. What patterns can you discern? Can you find any axes of (reflectional) symmetry? What should be the size of the fundamental (repeating) building blocks of symmetry in each case? Remember that you can post your answers in the comment field below, and in case you can't work them out, we'll publish the answers in a few weeks' time.
(Click on the images to see a larger version.)




Multiples of non-consecutive numbers
Next we use some non-consecutive values of $k$. The following figure uses blue for numbers that are multiples of $6$, and green for numbers that are multiples of $9$.(Click on the image to see a larger version.)

Here are a few more patterns for you to admire. In each case we colour the multiples of non-consecutive numbers. Can you tell what numbers these are and describe the patterns that emerge? Remember that you can post your answers in the comment field below, and in case you can't work them out, we'll publish the answers in a few weeks' time.
(Click on the images to see a larger version.)





Remainders
Finally, if we fix a number $k$ and assign colours to cells depending on their remainder with respect to $k$, then all the squares can be filled in. For example, let multiples of $5$ be black, numbers with a remainder $1$ with respect to $5$ be green, numbers with a remainder $2$ with respect to $5$ be red, numbers with a remainder $3$ with respect to $5$ be purple, and numbers with a remainder $4$ with respect to $5$ be yellow; the following figure is obtained.:(Click on the image to see a larger version.)

Conclusion
We've discovered some of the symmetries that hide within the multiplication table of positive integers. It's easy to create these patterns (for example, using Excel) and they can all be explained without much difficulty using the arithmetic of whole numbers and divisibility criteria. Displaying these symmetries using colours introduces a new facet to the maths. These images and others created in similar ways may appeal to students of mathematics and the arts, and may lead to new collaborations. At the very least such images may, we hope, intrigue, amaze, and inspire.
About this article
Zoheir Barka , from Laghouat in Algeria, is an amateur and self-educated mathematician. He has a Masters degree in French language from Laghouat University and is currently a French teacher in elementary school.
A version of this article first appeared as The hidden symmetries of the multiplication table in the Journal of Humanistic Mathematics, Volume 7, Issue 1 (January 2017), pages 189-203.