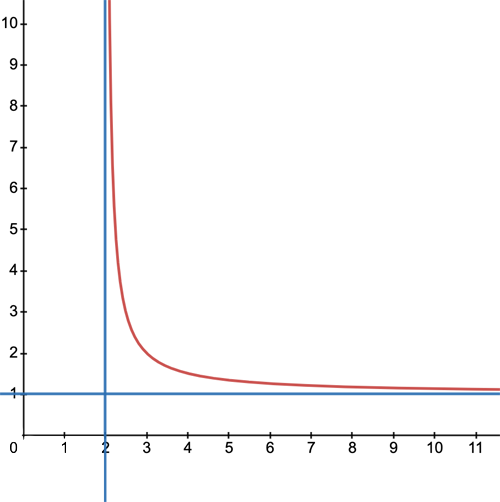
Not all curves look like a straight line as $x$ or $y$ tend to infinity, so not all curves have asymptotes. But if they do (and of you are comfortable with limits which you can read about here) then you can find the asymptotes by taking the limit of the function describing the curve as $x$ or $y$ tend to infinity. In our example above this gives $$\lim_{x \rightarrow \infty} y = \lim_{x \rightarrow \infty}\frac{1}{x-2}+1=1.$$ That gives you the horizontal asymptote. Rearranging the expression (1) to phrase it in terms of $y$ gives $$x=\frac{1}{y-1}+2,$$ so $$\lim_{y \rightarrow \infty} x = \lim_{y \rightarrow \infty}\frac{1}{y-1}+2=2.$$ This gives you the vertical asymptote.
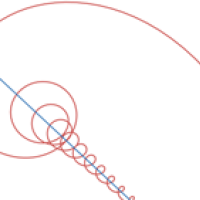
We leave you with an example of a pretty crazy curve and its perfectly uncrazy asymptote. The curve is given by a more complex \emph{parametric} equation $$x=t+\frac{\cos{(14t)}}{t}, y=t+\frac{\sin{(14t)}}{t}, t>0.$$ The asymptote (to the wriggly part of the curve) as $x$ goes to infinity is the line $y=x$.
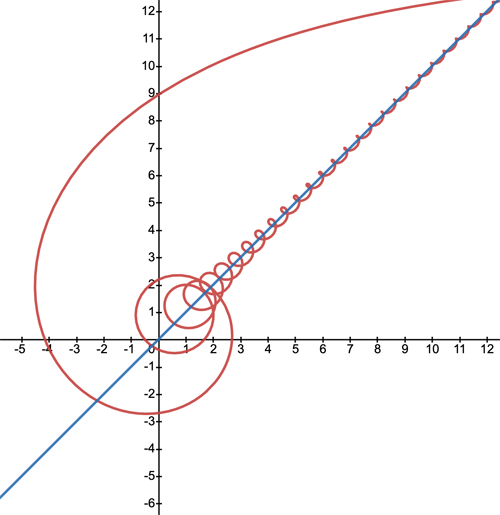
Thanks to Guillaume Jacquenot for posting this example on on Wikipedia.
This example again highlights how useful asymptotes are. It's not easy to work out the exact value of $y$ for a given $x$, but knowing the asymptote gives you a good approximation of $y$ for large $x$ — the larger $x$, the better the approximation.About this article
This article relates to the Applicable resurgent asymptotics research programme hosted by the Isaac Newton Institute for Mathematical Sciences (INI). You can see more articles relating to the programme here.
This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
