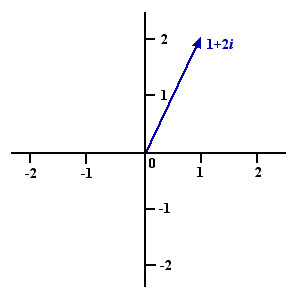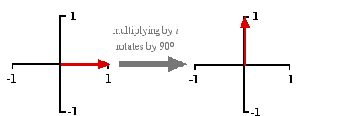Solving equations often involves taking square roots of numbers and if you're not careful you might accidentally take a square root of something that's negative. That isn't allowed of course, but if you hold your breath and just carry on, then you might eventually square the illegal entity again and end up with a negative number that's a perfectly valid solution to your equation.
People first noticed this fact in the 15th century. A lot later on, in the 19th century, William Rowan Hamilton noticed that the illegal numbers you come across in this way can always be written as $x+iy$ where $x $ and $y$ are ordinary numbers and $i$ stands for the square root of $-1.$ The number $i$ itself can be represented in this way with $x=0$ and $y=1.$ Numbers of this form are called complex numbers.
You can add two complex numbers like this:
$$(x+iy) + (u+iv) = (x+u) + i(y+v).$$
And you multiply them like this:
$$(x+iy)(u+iv) = xu + i(xv+yu) + i^2yv = xu - yv + i(xv+yu).$$
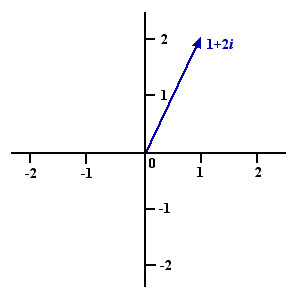
The complex number 1+2i.
But how can we visualise these numbers and their addition and multiplication? The $x$ and $y$ components are normal numbers so we can associate to them the point with coordinates $(x,y)$ on the plane, which is where you get to if you walk a distance $x$ in the horizontal direction and a distance $y$ in the vertical direction. So the complex number $(x+u) + i(y+v),$ which is the sum of $(x+iy)$ and $(u+iv),$ corresponds to the point you get to by walking a distance $x+u$ in the horizontal direction and a distance $y+v$ in the vertical direction. Makes sense.
What about multiplication? Think of the numbers that lie on your horizontal axis with coordinates $(x,0).$ Multiplying them by $-1$ flips them over to the other side of the point $(0,0)$: $(1,0)$ goes to $(-1,0),$ $(2,0)$ goes to $(-2,0),$ and so on. In fact, you can think of multiplication by $-1$ as a rotation: you rotate the whole plane through 180 degrees about the point $(0,0).$
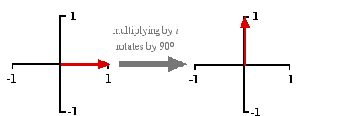
Multiplying by i.
What about multiplication by $i,$ the square root of $-1$? Multiplying twice by $i$ is the same as multiplying by $-1.$ So if the latter corresponds to a rotation through 180 degrees, the former should correspond to rotation by 90 degrees. And this works. Try multiplying any complex number, say $2+i5,$ by $i$ and you will see that the result corresponds to the point you get to by rotating through 90 degrees (counter-clockwise) about $(0,0).$
And what about multiplying not just by $i$ but by a more difficult complex number $u+iv?$ Well, multiplying by an ordinary positive number corresponds to stretching or shrinking the plane: multiplication by 2 takes a point $(x,y)$ to $(2x,2y)$ which is further away from $(0,0)$ (that's stretching) and multiplication by 1/2 takes it to $(x/2,y/2)$ which is closer to $(0,0)$ (shrinking).
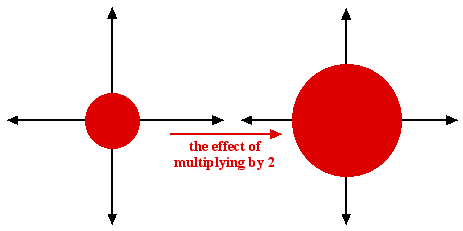
Multiplying by 2 is stretching.
It turns out that multiplication by a complex number $u+iv$ corresponds to a combination of rotation and shrinking/stretching. For example, multiplication by $-1+1.732i$ is rotation through 120 degrees followed by stretching by a factor of 2. So complex numbers are not just weird figments of the imagination designed to help you solve equations, they've got a geometric existence in their own right.
You can find out more about complex numbers and things you can do with them in this introductory package and in our teacher package.
Return to the Plus advent calendar 2021.
This article now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.