Euler's polyhedron formula

Leonhard Euler, 1707 - 1783
Let's begin by introducing the protagonist of this story — Euler's formula:
Simple though it may look, this little formula encapsulates a fundamental property of those three-dimensional solids we call polyhedra, which have fascinated mathematicians for over 4000 years. Actually I can go further and say that Euler's formula tells us something very deep about shape and space. The formula bears the name of the famous Swiss mathematician Leonhard Euler (1707 - 1783), who would have celebrated his 300th birthday this year.
What is a polyhedron?
Before we examine what Euler's formula tells us, let's look at polyhedra in a bit more detail. A polyhedron is a solid object whose surface is made up of a number of flat faces which themselves are bordered by straight lines. Each face is in fact a polygon, a closed shape in the flat 2-dimensional plane made up of points joined by straight lines.
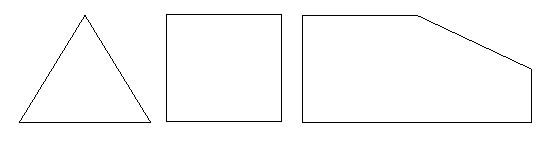
Figure 1: The familiar triangle and square are both polygons, but polygons can also have more irregular shapes like the one shown on the right.
Polygons are not allowed to have holes in them, as the figure below illustrates: the left-hand shape here is a polygon, while the right-hand shape is not.
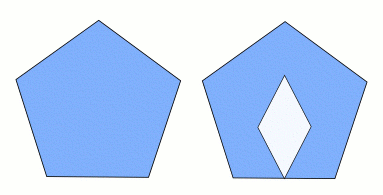
Figure 2: The shape on the left is a polygon, but the one on the right is not, because it has a 'hole'.
A polygon is called regular if all of its sides are the same length, and all the angles between them are the same; the triangle and square in figure 1 and the pentagon in figure 2 are regular.
A polyhedron is what you get when you move one dimension up. It is a closed, solid object whose surface is made up of a number of polygonal faces. We call the sides of these faces edges — two faces meet along each one of these edges. We call the corners of the faces vertices, so that any vertex lies on at least three different faces. To illustrate this, here are two examples of well-known polyhedra.
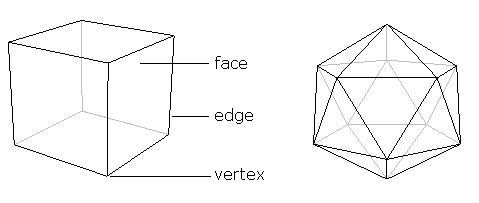
Figure 3: The familiar cube on the left and the icosahedron on the right. A polyhedron consists of polygonal faces, their sides are known as edges, and the corners as vertices.
A polyhedron consists of just one piece. It cannot, for example, be made up of two (or more) basically separate parts joined by only an edge or a vertex. This means that neither of the following objects is a true polyhedron.
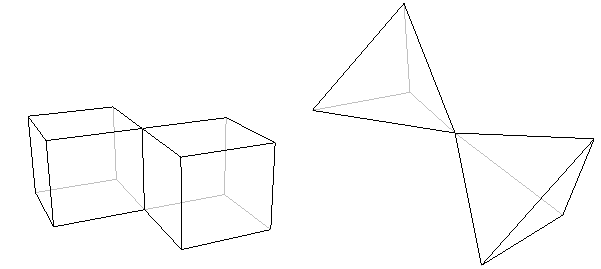
Figure 4: These objects are not polyhedra because they are made up of two separate parts meeting only in an edge (on the left) or a vertex (on the right).
What does the formula tell us?
We're now ready to see what Euler's formula tells us about polyhedra. Look at a polyhedron, for example the cube or the icosahedron above, count the number of vertices it has, and call this number V. The cube, for example, has 8 vertices, so V = 8. Next, count the number of edges the polyhedron has, and call this number E. The cube has 12 edges, so in the case of the cube E = 12. Finally, count the number of faces and call it F. In the case of the cube, F = 6. Now Euler's formula tells us that
or, in words: the number of vertices, minus the number of edges, plus the number of faces, is equal to two.
In the case of the cube, we've already seen that V = 8, E = 12 and F = 6. So,
which is what Euler's formula tells us it should be. If we now look at the icosahedron, we find that V = 12, E = 30 and F = 20. Now,
Euler's formula is true for the cube and the icosahedron. It turns out, rather beautifully, that it is true for pretty much every polyhedron. The only polyhedra for which it doesn't work are those that have holes running through them like the one shown in the figure below.
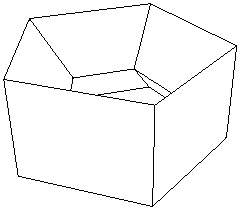
Figure 5: This polyhedron has a hole running through it. Euler's formula does not hold in this case.
These polyhedra are called non-simple, in contrast to the ones that don't have holes, which are called simple. Non-simple polyhedra might not be the first to spring to mind, but there are many of them out there, and we can't get away from the fact that Euler's Formula doesn't work for any of them. However, even this awkward fact has become part of a whole new theory about space and shape.
The power of Euler's formula
Whenever mathematicians hit on an invariant feature, a property that is true for a whole class of objects, they know that they're onto something good. They use it to investigate what properties an individual object can have and to identify properties that all of them must have. Euler's formula can tell us, for example, that there is no simple polyhedron with exactly seven edges. You don't have to sit down with cardboard, scissors and glue to find this out — the formula is all you need. The argument showing that there is no seven-edged polyhedron is quite simple, so have a look at it if you're interested.
Using Euler's formula in a similar way we can discover that there is no simple polyhedron with ten faces and seventeen vertices. The prism shown below, which has an octagon as its base, does have ten faces, but the number of vertices here is sixteen. The pyramid, which has a 9-sided base, also has ten faces, but has ten vertices. But Euler's formula tells us that no simple polyhedron has exactly ten faces and seventeen vertices.
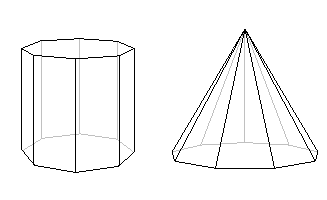
Figure 6: Both these polyhedra have ten faces, but neither has seventeen vertices.
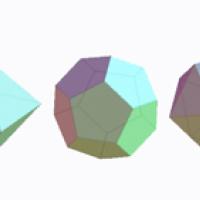
It's considerations like these that lead us to what's probably the most beautiful discovery of all. It involves the Platonic Solids, a well-known class of polyhedra named after the ancient Greek philosopher Plato, in whose writings they first appeared.
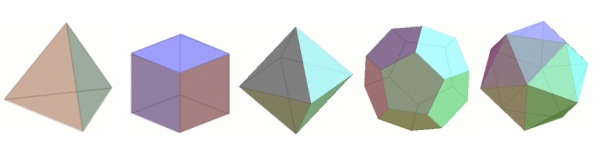
Figure 7: The Platonic solids. From left to right we have the tetrahedon with four faces, the cube with six faces, the octahedron with eight faces, the dodecahedron with twelve faces, and the icosahedron with twenty faces.
Although their symmetric elegance is immediately apparent when you look at the examples above, it's not actually that easy to pin it down in words. It turns out that it is described by two features. The first is that Platonic solids have no spikes or dips in them, so their shape is nice and rounded. In other words, this means that whenever you choose two points in a Platonic solid and draw a straight line between them, this piece of straight line will be completely contained within the solid — a Platonic solid is what is called convex. The second feature, called regularity, is that all the solid's faces are regular polygons with exactly the same number of sides, and that the same number of edges come out of each vertex of the solid.
The cube is regular, since all its faces are squares and exactly three edges come out of each vertex. You can verify for yourself that the tetrahedron, the octahedron, the icosahedron and the dodecahedron are also regular.
Now, you might wonder how many different Platonic Solids there are. Ever since the discovery of the cube and tetrahedron, mathematicians were so attracted by the elegance and symmetry of the Platonic Solids that they searched for more, and attempted to list all of them. This is where Euler's formula comes in. You can use it to find all the possibilities for the numbers of faces, edges and vertices of a regular polyhedron.What you will discover is that there are in fact only five different regular convex polyhedra! This is very surprising; after all, there is no limit to the number of different regular polygons, so why should we expect a limit here? The five Platonic Solids are the tetrahedron, the cube, the octahedron, the icosahedron and the dodecahedron shown above.
The proof

René Descartes,
(1596 - 1650)
Playing around with various simple polyhedra will show you that Euler's formula always holds true. But if you're a mathematician, this isn't enough. You'll want a proof, a water-tight logical argument that shows you that it really works for all polyhedra, including the ones you'll never have the time to check.

Adrien-Marie Legendre, (1752 - 1833)
Despite the formula's name, it wasn't in fact Euler who came up with the first complete proof. Its history is complex, spanning 200 years and involving some of the greatest names in maths, including René Descartes (1596 - 1650), Euler himself, Adrien-Marie Legendre (1752 - 1833) and Augustin-Louis Cauchy (1789 - 1857).

Augustin-Louis Cauchy, (1789 - 1857)
It's interesting to note that all these mathematicians used very different approaches to prove the formula, each striking in its ingenuity and insight. It's Cauchy's proof, though, that I'd like to give you a flavour of here. His method consists of several stages and steps. The first stage involves constructing what is called a network.
Forming a network
Imagine that you're holding your polyhedron with one face pointing upward. Now imagine "removing" just this face, leaving the edges and vertices around it behind, so that you have an open "box". Next imagine that you can hold onto the box and pull the edges of the missing face away from one another. If you pull them far enough the box will flatten out, and become a network of points and lines in the flat plane. The series of diagrams below illustrates this process as applied to a cube.
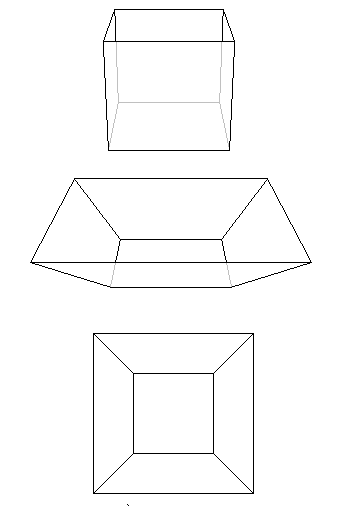
Figure 8: Turning the cube into a network.
As you can see from the diagram above, each face of the polyhedron becomes an area of the network surrounded by edges, and this is what we'll call a face of the network. These are the interior faces of the network. There is also an exterior face consisting of the area outside the network; this corresponds to the face we removed from the polyhedron. So the network has vertices, straight edges and polygonal faces.
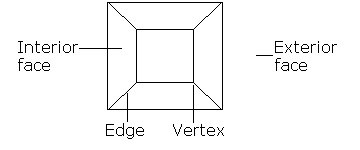
Figure 9: The network has faces, edges and vertices.
When forming the network you neither added nor removed any vertices, so the network has the same number of vertices as the polyhedron — V. The network also has the same number of edges — E — as the polyhedron. Now for the faces; all the faces of the polyhedron, except the "missing" one, appear "inside" the network. The missing face has become the exterior face which stretches away all round the network. So, including the exterior face, the network has F faces. Thus, you can use the network, rather than the polyhedron itself, to find the value of V - E + F. We'll now go on to transform our network to make this value easier to calculate.
Transforming the Network
There are three types of operation which we can perform upon our network. We'll introduce three steps involving these.
Step 1 We start by looking at the polygonal faces of the network and ask: is there a face with more than three sides? If there is, we draw a diagonal as shown in the diagram below, splitting the face into two smaller faces.
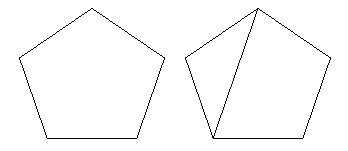
Figure 10: Dividing faces.
We repeat this with our chosen face until the face has been broken up into triangles.
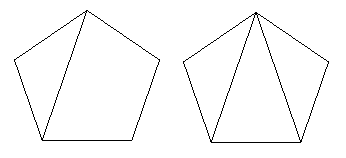
Figure 11: In the end we are left with triangular faces.
If there is a further face with more than three sides, we use Step 1 on that face until it too has been broken up into triangular faces. In this way, we can break every face up into triangular faces, and we get a new network, all of whose faces are triangular. We illustrate this process by showing how we would transform the network we made from a cube.
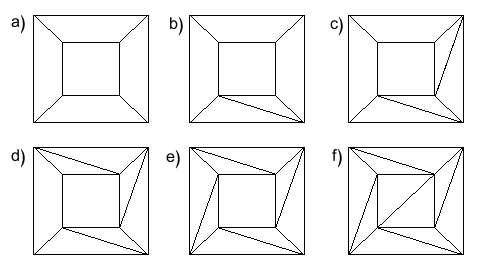
Figure 12: This is what happens to the cube's network as we repeatedly perform Step 1.
We go back to Step 1, and look at the network we get after performing Step 1 just once. Now, by drawing a diagonal we added one edge. Our original face has become two faces, so we have added one to the number of faces. We haven't changed the number of vertices. The network now has V vertices, E + 1 edges and F + 1 faces. So how has V - E + F changed after we performed Step 1 once? Using what we know about the changes in V, E and F we can see that V - E + F has become V - (E + 1) + (F + 1). Now we have
So V - E + F has not changed after Step 1! Because each use of Step 1 leaves V - E + F unchanged, it is still unchanged when we reach our new network made up entirely of triangles! The effect on V - E + F as we transform the network made from the cube is shown in the table below.
| Round | V | E | F | V - E + F |
| (a) | 8 | 12 | 6 | 2 |
| (b) | 8 | 13 | 7 | 2 |
| (c) | 8 | 14 | 8 | 2 |
| (d) | 8 | 15 | 9 | 2 |
| (e) | 8 | 16 | 10 | 2 |
| (f) | 8 | 17 | 11 | 2 |
We now introduce Steps 2 and 3. They will remove faces from around the outside of the network, reducing the number of faces step by step. Once we begin to do this the network probably won't represent a polyhedron anymore, but the important property of the network is retained.
Step 2 We check whether the network has a face which shares only one edge with the exterior face. If it does, we remove this face by removing the one shared edge. The area which had been covered by our chosen face becomes part of the exterior face, and the network has a new boundary. This is illustrated by the diagram below for the network made from the cube.
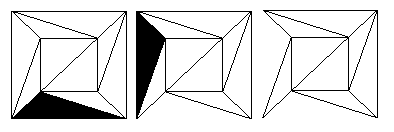
Figure 13: Removing faces with one external edge.
Now, we will take V, E and F to be the numbers of vertices, edges and faces the network made up of triangular faces had before we performed Step 2. We now look at how the number V - E + F has changed after we perform Step 2 once. We have removed one edge, so our new network has E - 1 edges. We have not touched the vertices at all, so we still have V vertices. The face we used for Step 2 was merged with the exterior face, so we now have F - 1 faces. So V - E + F has become V - (E - 1) + (F - 1) and
So once again V - E + F has not changed.
Step 3 We check whether our network has a face which shares two edges with the exterior face. If it does, we remove this face by removing both these shared edges and their shared vertex, so that again the area belonging to our chosen face becomes part of the exterior face. This is illustrated below in the case of the network made from the cube, as it is after performing Step 2 twice.
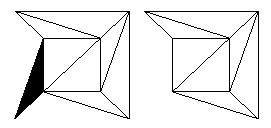
Figure 14: Removing faces with two external edges.
As we did before we now take V, E and F to be the numbers of vertices, edges and faces of the network we're starting with. Now how has the number V - E + F been affected by Step 3? We have removed one vertex — the one between the two edges — so there are now V - 1 vertices. We have removed two edges, so there are now E - 2 edges. Finally, our chosen face has merged with the exterior face, so we now have F - 1 faces. So V - E + F has become (V - 1) - (E - 2) - (F - 1) and
So once more V - E + F has not changed.
The secret of the proof lies in performing a sequence of Steps 2 and 3 to obtain a very simple network. Recall that we had repeatedly used Step 1 to produce a network with only triangular faces. This network will definitely have a face which shares exactly one edge with the exterior face, so we take this face and perform Step 2. We can perform Step 2 on several faces, one at a time, until a face sharing two edges with the exterior face appears. We can then perform Step 3 using this face. We carry on performing Steps 2 and 3, and keep removing faces in this way.
There are two important rules to follow when doing this. Firstly, we must always perform Step 3 when it's possible to do so; if there's a choice between Step 2 and Step 3 we must always choose Step 3. If we do not, the network may break up into separate pieces. Secondly, we must only remove faces one at a time. If we don't we may end up with edges sticking out on their own into the exterior face, and we'll no longer have a proper network. To illustrate the process, we'll perform several steps on the cube network, continuing from where we left it in the last diagram.
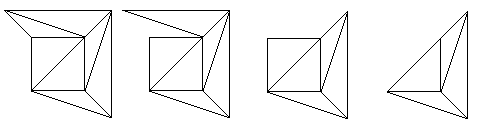
Figure 15: Applying our algorithm to the network of the cube.
Now we can ask ourselves one or two questions. Does this process of removing faces ever stop, and, if it does, what are we left with? A little consideration will show you that it must stop — there are only finitely many faces and edges we can remove — and that when it does, we are left with a single triangle. You can see some diagrams describing the whole process for the network formed from a dodecahedron (recall that this was one of the Platonic solids introduced earlier).
Now look at the numbers of vertices, edges and faces present in our final network — the single triangle. We have V=3, E=3, and F=2 — we must still include the exterior face. Now
Throughout the whole process, starting with the complete polyhedron and ending with a triangle, the value of V - E + F has not changed. So if V - E + F = 2 for the final network, we must also have V - E + F = 2 for the polyhedron itself! The proof is complete!
Beyond polyhedra
I will finish by mentioning some consequences of Euler's formula beyond the world of polyhedra. I'll start with something very small: computer chips. Computer chips are integrated circuits, made up of millions of minute components linked by millions of conducting tracks. These are reminiscent of our networks above, except that usually it is not possible to lay them out in a plane without some of the conducting tracks — the edges — crossing. Crossings are a bad thing in circuit design, so their number should be kept down, but figuring out a suitable arrangement is no easy task. Euler's polyhedron formula, with its information on networks, is an essential ingredient in finding solutions.
Now let's move to the very large: our universe. To this day cosmologists have not agreed on its exact shape. Pivotal to their consideration is topology, the mathematical study of shape and space. In the 19th century mathematicians discovered that all surfaces in three-dimensional space are essentially characterised by the number of holes they have: our simple polyhedra have no holes, a doughnut has one hole, etc. Euler's formula does not work for polyhedra with holes, but mathematicians discovered an exciting generalisation. For any polyhedron, V - E + F is exactly 2 minus 2 times the number of holes! It turns out that this number, called the Euler characteristic, is crucial to the study of all three-dimensional surfaces, not just polyhedra. Euler's formula can be viewed as the catalyst for a whole new way of thinking about shape and space.
About the author

Abi grew up in the north of England, and moved south to study maths at Imperial College, London, and Queen Mary, University of London. She now teaches maths at the Open University. Abi's main mathematical interest is group theory. She has really enjoyed exploring the mysteries of Euler's formula when writing this article.
Originally published on 1 June 2007
Comments
Anonymous
it is really a breif but very usefull article.
Regards
A. Minhaj
Secondary Maths Teacher
AIC, Perth, W. Australia
Y SrinivasaRao
Very useful matter and useful for research scholar's in-depth.
Anonymous
Very, very useful and well explained!
Anonymous
Thank you so much:) I'm doing a math project on polyhedra and this was the most helpful website by far =]
Anonymous
Very well done, succinct and clear, and in a friendly voice. I will be showing this to my son, who has recently asked me about how to prove the formula.
Best wishes to you, Abi.
Mark from Seattle
Anonymous
thanks! was really useful!
i liked the step for step explanations.
Anonymous
how did you get 14-12? i dont see it!!!
swob
they added the 8 and the 6 first then took 12 away
Anonymous
She did the 8 + 6 first giving a total of 14 and than subtracted the 12
as in using BEDMAS
but in this case it will work if you just go from left to right
Anonymous
I was asked to research this for homework, and this is the most helpful site I have found about Euler's mathematical theorems.
It really helped me out:)
thanks
Anonymous
Great article. Good if you just need a quick look for a math contest prep or for research. =D I hope you write others like this Abi!
Anonymous
Hi
I have a question - actually it is a question in an assignment: If a solid has 6 faces, what are the possible combinations of vertices and edges it can have?
Using Euler's formula:
V-E+F = 2
=> V-E+6=2
=> 4 = E-V
Which to me says: an unlimited number as long as the difference between the number of Edges and Vertices is always 4. But logically this does not make sense. Please help?
Anonymous
Maybe you would have to experiment using 'sides' of the polyhedron's faces, the way she did here, in proving no polyhedron has seven edges:
http://plus.maths.org/content/os/issue43/features/kirk/proof
but as I could barely follow *that* one, that's all the 'help' I can offer :)
Anonymous
well the question specifically states that what are the possible combinations.. which clearly means there would be an infinite number of solutions..so after the reccomendation of your teacher, you can ask him/her if you could write just a few pairs..thats what i did...
Anonymous
V-E+6=2,
so if you solve it you get
V=-4+E
and E=4+V
see not infinite :)
Anonymous
I think we must have an upper bound of no.of sides for a given no.of faces. It should be (n C 2) for n no. of sides, as 2 faces merge at 1 side.
Satyaki Bhattacharya
student of class xi
India
Sreenadh
Think of a cube. This has 6 faces, 12 edges and 8 vertices, so E-V=4
Now take one of the edges, and add a midpoint vertex. This divides the edge into two, so you also end up adding an edge ( and two of the faces now have 5 edges instead of 4, but that is irrelevant) So now you have E=13,V=9 and still E-V=4
It is clear that this can be repeated as many times as you want. So yes, there are really an unlimited number of possibilities!
oliver
2-6=-4 not 4
Alexander Griessel
Hi! The answer is simple- you can take any edge on the cube, and add a vertex along its length. You've now added one vertex and one edge. This step can be repeated as often as you want.
*-------------*
| |
| |
| |
| |
*-------------*
*-------------*
| |
| |
* |
| |
| |
*-------------*
Anonymous
Fantastic !!!!
A just fabulous pice of work.
Miguel Bader
Maths Teacher
Australia
Anonymous
by far most simple and amazing explanation that i have come across.
Great article
Anonymous
I am only in year 7 but have been very interested in the idea of 3-D. This article is full of amazing facts.
Thanks
Anonymous
Wait you are only 7 years old???
plusadmin
UK school year 7 students are 11-12 years old
Anonymous
He is in seventh grade.
Anonymous
OK HERE IS MY QUESTION
USE EULER'S FORMULA TO ANSWER THE QUESTION
A POLYHEDRA HAS 14 VERTICES AND 16 FACES HOW MANY EDGES DOES IT HAVE?
I KNOW YOU DO THIS
14-E+16=2
BUT WHAT ELSE DO I DO?
Marianne
You need to solve the equation for E to get the number of edges.
Anonymous
14-E+16=2
14+16=E
14+16-2=E
30-2=E
28=E
Krish
14-E = -14
-E = -28
E = 28
Anonymous
Using the fact that every vertex 'u' is connected to d(u) (degree of 'u') faces of the polyhedron, we try and see what happens to |V|,|F| and |E| when a vertex is removed and a new polyhedron is formed with |V'| , |F'| and |E'| (# of vertices, faces and edges).
|V'|= |V|-1 (trivial)
|F'|=|F|-d(u)+1
all the d(u) faces vertex 'u' is connected to will merge into a single face
|E'|=|E|-d(u) (trivial)
observe that |V|+|F|-|E|=|V'|+|F'|-|E'|
repeat this process on the given polyhedron until only a cycle is left.
And we can see that |V|+|F|-|E|=2
(the face formed by merging the faces to be removed and the face already present is the same, i.e our cycle has two faces)
Anonymous
Figure 2: The shape on the left is a polygon, but the one on the right is not, because it has a 'hole'
My question is:
of the regular polygons which have "holes" which are polygon themselves?
And, what kind of regular polygons are "holes" to other polygones?
Anonymous
what about for a sphere, cone and cylinder?
Anonymous
Consider that a cone is what you get if you take a pyramid with a base formed by a polygon, and increase the number of polygon sides to a very large number. A little more formally, if we represent the number of sides of the base polygon with n (we'll call the polygon an n-gon, following the form of a pentagon, a hexagon, etc), then we say that a cone is the limit of our n-gon pyramid as n goes to infinity.
The number of sides of an n-gon is n, by definition, and the number of vertices is also n. As the base of the pyramid, the n-gon is one face.
We add one more vertex at the top of the pyramid, so we have V = n + 1.
We draw n more edges, from the new vertex to each of the n vertices on the n-gon. So, we have E = n + n.
Those new edges define n new faces, one between the vertex and each of the n sides of the cone, so we have F = 1 + n.
Then, we want the limit as n goes to infinity of V - E + F.
lim (V - E + F)
n→∞
lim [(n+1) - (n+n) + (1+n)]
n→∞
The n's cancel out, and we're left with
lim [2]
n→∞
which is simply 2.
You can do a similar thing with a cylinder, considering it to be the limit of a prism with an n-gon base as n goes to infinity.
A sphere is tougher to visualize, but you can consider it the limit of a regular n-hedron as n goes to infinity, and it will still satisfy V - E + F = 2.
gregdavid
Awesome and very elegant proof especially as we know that all closed convex surgaces (n-gon's) must satisfy Eulers equation.
My math skills aren't what they used to be, so instead of using calculus, I cheat. I tend to just imagine a cylinder as a rectangle when when its curved face is cut & flattened. Then consider it to be one face and where the two side edges of that rectanglular face met as a third edge, and where that 3rd edge intersects the 2 top & bottom circular edges as 2 vertices. Doing so, Euler's formula is satisfied. V-E+F=2-3+3=2.
For the closed cone if cut down the face perpendicular to the bottom edge, it flattens out to an isosceles triangle so again one extra edge where those two sides meet and a verticie at each end. Si with only 2 faces, 2 verifies and 2 edges again Eulers equation is satisfied.
For the open cone, that loses a bottom face. You have to count the inner face instead.
For the sphere I realize you make one by rotating a semi circle around an axis 360°. So I consider the arc that they meet at 0° & 360° (or the axis of rotation) as an edge, with the two poles at it's endpoints. So with one face, one edge and 2 verticies, again Eulers equation holds.
Anonymous
Hello,
These solids do not have faces, which must have edges (line segments). So Euler's formula cannot be applied.
Hope this helps.
Mel
Ashleigh
Polyhedron must have flat surfaces
Ashleigh Yr8
Anonymous
Awesome article it helped me so much with my homework Thanks Abi and hope you like teaching!
Anonymous
You said only polyhedra with holes don't follow euler's formula, this seems to be true by the definition that you are using. But I think many people call some nonconvex polyhedra like the ones you eliminated... well, like I said "nonconvex polyhedra". In which case their Euler characteristic would not be 2.
But that is not too important, I thought it might be instructive for some people to see an example of something that some people call a polyhedron (but it wouldn't be under your definition) but to a non mathematicion, might seem like a perfectly reasonable solid to be called such. So if you take two cubes, one smaller than the other, joined at a face so that the smaller cube is not touching any of the bigger cubes big edges. This has Euler Characteristic 3 instead of 2. Great article, just thought people might be interested to know about what restricting faces to being polygons leas you to. Of course there are some nonconvex polyhedra with polygonal sides that do have euler characteristic that isn't 2, but these don't satisfy you condtion about having parts seperated by a 1 manifold. Great article!
Anonymous
I implied that Polygons, cant have holes, but most mathematicians define them so that they can have holes. Anyways, I think you defined them the former, way so I was going with that. In the latter case, my example of a non convex polyhedron with Euler characteristic 3 is a pretty useful one.
Anonymous
Is there a polyhedrion with 10 edges and 6 vertices? (and 6 faces, of course, according to Euler's formula)
Guilherme
guilherme.campos@ua.pt
Anonymous
A pentagonal pyramid consists of 6 faces, 6 vertices and 10 edges (including the base)
Anonymous
Does Euler's formular, generalized for n-dimensions, exist?
Anonymous
This article really helped me with my homework, but what I don't get is can polygon have holes in them or not? A lot of the comments say they can but the article says no. It is not so important to know for my homework but I am just a bit interested in it.
Anonymous
Thank you so much! I haven't been able to find another website that explained Cauchy's proof that made it so easy to understand. This really helped with my project.
Anonymous
This is a wonderful read. I am not a math major, but I am authorized to teach foundational-level mathematics. This helped me understand Euler's theorem much better so that I could teach it to my advanced geometry students.
Anonymous
You might find this interesting:
https://www.awesomemath.org/assets/PDFs/MR4_planar_graphs.pdf
Anonymous
Round V E F V - E + F
(a) 8 12 6 2
(b) 8 13 7 2
(c) 8 14 8 2
(d) 8 15 9 2
(e) 8 16 10 2
(f) 8 16 11 2
I think that 8+16-11 doesn't equal to 2
so that part is a bit confusing.
Anonymous
The final edge added in round f) brings the number E up to 17. One can count the edges in f) in the illo. Therefore the table must contain a typo.
Anonymous
Oh. It is supposed to be 17 edges. When I saw that, it didn't seem right. However it was just a mistake. If you count the number of edges in drawing "F", you'll see that its 17. So 8-17+11=2.
Also you made a mistake here:
"I think that 8+16-11 doesn't equal to 2
so that part is a bit confusing". It should be 8-16+11 because the formula is V-E+F or in this case 8-16+11.
Anonymous
V+F-E=2
8+11-16=3?
What polyhedron are you typing about?