
The golden ratio and aesthetics
Mario Livio is a scientist and self-proclaimed "art fanatic" who owns many hundreds of art books. Recently, he combined his passions for science and art in two popular books, The Accelerating Universe, which appeared in 2000, and The Golden Ratio, reviewed in this issue of Plus. The former book discusses "beauty" as an essential ingredient in fundamental theories of the universe. The latter discusses the amazing appearances of the peculiar number 1.618... in nature, the arts, and psychology. Here he gives us a taster.
The origins of the divine proportion
In the Elements, the most influential mathematics textbook ever written, Euclid of Alexandria (ca. 300 BC) defines a proportion derived from a division of a line into what he calls its "extreme and mean ratio." Euclid's definition reads:
A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.In other words, in the diagram below, point C divides the line in such a way that the ratio of AC to CB is equal to the ratio of AB to AC. Some elementary algebra shows that in this case the ratio of AC to CB is equal to the irrational number 1.618 (precisely half the sum of 1 and the square root of 5).
C divides the line segment AB according to the Golden Ratio
Who could have guessed that this innocent-looking line division would have implications for numerous natural phenomena ranging from the leaf and seed arrangements of plants to the structure of the crystals of some aluminium alloys, and from the arts to the stock market?

Sunflower seeds
In fact, with the increasing realization of the astonishing properties of this number over the centuries since Euclid's definition, the number was given the honorifics "Divine Proportion" and "Golden Ratio."
Here I shall concentrate only on one of the surprising (claimed) attributes of the Golden Ratio - its presumed association with aesthetics, since it provides a wonderful example of an attempt to mingle mathematics with the arts.
The golden ratio in the arts
Many books claim that if you draw a rectangle around the face of Leonardo da Vinci's Mona Lisa, the ratio of the height to width of that rectangle is equal to the Golden Ratio. No documentation exists to indicate that Leonardo consciously used the Golden Ratio in the Mona Lisa's composition, nor to where precisely the rectangle should be drawn. Nevertheless, one has to acknowledge the fact that Leonardo was a close personal friend of Luca Pacioli, who published a three-volume treatise on the Golden Ratio in 1509 (entitled Divina Proportione).

Sacrament of the Last Supper, by Salvador Dali
Another painter, about whom there is very little doubt that he actually did deliberately include the Golden Ratio in his art, is the surrealist Salvador Dali. The ratio of the dimensions of Dali's painting Sacrament of the Last Supper is equal to the Golden Ratio. Dali also incorporated in the painting a huge dodecahedron (a twelve-faced Platonic solid in which each side is a pentagon) engulfing the supper table. The dodecahedron, which according to Plato is the solid "which the god used for embroidering the constellations on the whole heaven," is intimately related to the Golden Ratio - both the surface area and the volume of a dodecahedron of unit edge length are simple functions of the Golden Ratio.
These two examples are only the tip of the iceberg in terms of the appearances of the Golden Ratio in the arts. The famous Swiss-French architect and painter Le Corbusier, for example, designed an entire proportional system called the "Modulor," that was based on the Golden Ratio. The Modulor was supposed to provide a standardized system that would automatically confer harmonious proportions to everything, from door handles to high-rise buildings. But why would all of these artists (there are many more than mentioned above) even consider incorporating the Golden Ratio in their works? The attempts to answer this question have led to a long series of psychological experiments, designed to investigate a potential relationship between the human perception of "beauty" and mathematics.
Is beauty in the eye of the beholder?
The pioneering (rather crude) experiments in this field were conducted by the German physicist and psychologist Gustav Theodor Fechner in the 1860s. Fechner's experiment was simple: ten rectangles varying in their length-to-width ratios were placed in front of a subject, who was asked to select the most pleasing one. The results showed that 76% of all choices centered on the three rectangles having ratios of 1.75, 1.62, and 1.50, with a peak at the "Golden Rectangle" (with ratio 1.62). Fechner went further and measured the dimensions of thousands of rectangular-shaped objects (windows, picture frames in the museums, books in the library), and claimed (in his book Vorschule der Aesthetik) to have found the average ratio to be close to the Golden Ratio.
Many psychologists have repeated similar experiments since then, and obtained rather conflicting results. Michael Godkewitsch of the University of Toronto, for example, pointed out that average group preferences often do not reflect the most preferred choice. For example, the brand of tea that everybody ranks second-best may on the average be rated best, but nobody will ever buy it. Godkewitsch therefore noted that first choices provide a more meaningful measure of preference than averages. Godkewitsch concluded from a study conducted in 1974 that the preference for the Golden Rectangle reported in the earlier experiments was an artifact of the rectangle's position in the range of rectangles presented to the subjects. He noted: "The basic question whether there is or is not, in the Western world, a reliable verbally expressed aesthetic preference for a particular ratio between length and width of rectangular shapes can probably be answered negatively."
Other experiments, however, gave different results. In particular, British psychologist Chris McManus concluded in 1980 that: "There is moderately good evidence for the phenomenon which Fechner championed." Nevertheless, McManus acknowledged that "whether the Golden Section [another name for the Golden Ratio] per se is important, as opposed to similar ratios (e.g. 1.5, 1.6 or even 1.75), is very unclear."
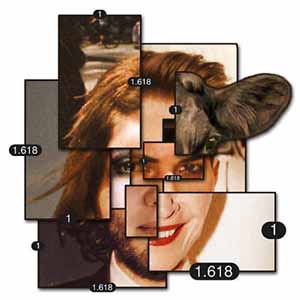
The entire topic received a new twist with a flurry of psychological attempts to determine the origin of facial attractiveness. For example, psychologist Judith Langlois of the University of Texas at Austin and her collaborators tested the idea that a facial configuration that is close to the population average is fundamental to attractiveness. Langlois digitized the faces of male and female students and mathematically averaged them, creating two-, four-, eight-, sixteen-, and thirty-two-face composites. College students were then asked to rate the individual and composite faces for attractiveness. Langlois found that the 16- and 32-averaged faces were rated significantly higher than individual faces. Langlois explained her findings as being broadly based on natural selection (physical characteristics close to the mean having been selected during the course of evolution), and on "prototype theory" (prototypes being preferred over non-prototypes).
Science writer Eric Haseltine claimed (in an article in Discover magazine in September 2002) to have found that the distance from the chin to the eyebrows in Langlois's 32-composite faces divides the face in a Golden Ratio. A similar claim was made in 1994 by orthodontist Mark Lowey, then at University College Hospital in London. Lowey made detailed measurements of fashion models' faces. He asserted that the reason we classify certain people as beautiful is because they come closer to Golden Ratio proportions in the face than the rest of the population.
Many disagree with both Langlois's and Lowey's conclusions. Psychologist David Perret of the University of St. Andrews, for example, published in 1994 the results of a study that showed that individual attractive faces were preferred to the composites. Furthermore, when computers were used to exaggerate the shape differences away from the average, those too were preferred. Perret claimed to have found that his beautiful faces did have something in common: higher cheek bones, a thinner jaw, and larger eyes relative to the size of the face.
An even larger departure from the "averageness" hypothesis was found in a study by Alfred Linney from the Maxillo Facial Unit at University College Hospital. Using lasers to make precise measurements of the faces of top models, Linney and his colleagues found that the facial features of the models were just as varied as those in the rest of the population.
I will certainly not attempt to make the ultimate sense of sex appeal in an article on the Golden Ratio. I would like to point out, however, that the human face provides us with hundreds of lengths to choose from. If you have the patience to juggle and manipulate the numbers in various ways, you are bound to come up with some ratios that are equal to the Golden Ratio.
Furthermore, I should note that the literature is bursting with false claims and misconceptions about the appearance of the Golden Ratio in the arts (e.g. in the works of Giotto, Seurat, Mondrian). The history of art has nevertheless shown that artists who have produced works of truly lasting value are precisely those who have departed from any formal canon for aesthetics. In spite of the Golden Ratio's truly amazing mathematical properties, and its propensity to pop up where least expected in natural phenomena, I believe that we should abandon its application as some sort of universal standard for "beauty," either in the human face or in the arts.
About the author

Dr. Mario Livio is the Head of the Science Division at the Space Telescope Science Institute (STScI), the institute which conducts the scientific program of the Hubble Space Telescope. He received his Ph.D. in theoretical astrophysics from Tel Aviv University in Israel, was a professor in the Physics Dept. of the Technion-Israel Institute of technology from 1981 till 1991, and joined STScI in 1991. Dr Livio has published over 300 scientific papers and received numerous awards for research and for excellence in teaching.
His interests span a broad range of topics in astrophysics, from cosmology to the emergence of intelligent life. Dr. Livio has done much fundamental work on the topic of accretion of mass onto black holes, neutron stars, and white dwarfs, as well as on the formation of black holes and the possibility to extract energy from them. During the past two years Dr. Livio's research focused on supernova explosions and their use in cosmology to determine the rate of expansion of the universe. In particular, he has shown that in spite of some uncertainties that still exist in theoretical models for supernovae, it is very likely that the recent findings that the expansion of our universe is accelerating are correct.
Comments
Anonymous
Dear Dr. Livio,
Thank you for the page with the wealth of information on the Golden Section.
I am a researcher in music cognition. My explanation of a space of music includes calling the Pythagorean intervals the melodic reference elements or artistic universals in music. The sharing of the "strong" spectral information between tones of the Pythagorean intervals is most likely the origin of their auditory pleasantness. From a perspective of neurophysiology, it is possible that the sharing (and the supposed relative ease in processing of these intervals) is related to the lesser cost of neural processing as compared to non-consonant compounds. Most likely, these neuropsychological properties were the foundation for a paleo-scale; they were of importance for the musician’s ear just 400 years ago. Yet today we listen to the slightly mistuned intervals which lost their sonic purity with the introduction of tempered scale.
I am an admirer of Matyla Ghyka and I really like his ideas of "built-into" geometrical universals (for example, log relations) which, I believe, affect our perception of the world.
It is possible that some ratios of natural growth are inherent for our perception.
Best,
Marina
Marina Korsakova-Kreyn, PhD
mnkors@gmail.com
Anonymous
good work!
Anonymous
The ratio of beautiful people to all people is likely phi.
Anonymous
But which group has the value of 1.618 and which has the value of 1?
-Preston Gull
Ryan Hartman
Forgive me if I'm totally wrong(I'm very new to even beginning to understand Phi), but I assume that he means the inverse, which is .618... this would allow the ratio to fit into a proper fraction instead of the improper 1.618 over 1. In this case the ratio of outwardly "beautiful" people would be the smaller of the two fractions, .382.
Anonymous
I am very impressed with your explanation and historical review of the Golden Ratio since the 15th Century, however I am disappointed that you did not go further back to India and the Far East where The golden ratio using the 9 Hindu numerals discovered by Fibonacci existed for centuries and thousands of years. There you would have found a wealth of information regarding the use of the Golden Ratio, particularly in the way the monuments, the places and castles were built. There before Columbus the people designed magic squares called yantras that used the measurement of the Golden Ratio. All this history is missing in your book , I hope that one day you will write book two on this topic. I found your books interesting...
Swami Ram Charran
Arun Tyagi
Can you give the reference where it can be studied
Anonymous
Wow... ! -
Michelle Tygielski :)
Anonymous
Why is your portrait not presented in the "golden" aspect ratio?
Anonymous
because the proportion of head/body to background is?
Anonymous
Please correct your erroneous statement that "Some elementary algebra shows that in this case the ratio of AC to CB is equal to the irrational number 1.618 (precisely half the sum of 1 and the square root of 5)". 1.618 is not an irrational number, nor is it equal to the golden ratio. A better statement would be ""Some elementary algebra shows that in this case the ratio of AC to CB is equal to an irrational number approximately equal to 1.618 (the ratio is precisely half the sum of 1 and the square root of 5)"
Anonymous
We all know what the author meant. We often talk about 1.618 meaning the number phi, because it is too long-winded to utter more decimal places or to be precise about the number. Imagine how long it would take to say 'A half plus half of the square root of five' every time we wished to refer to the number - ten syllables instead of five. Would Anonymous be satisfied with 'One point six one eight dot dot dot' instead? Do we have the permission of Anonymous to give this in print using the ellipsis: 1.618 ... ?
Chris G
A geometric sequence with a common ratio (or ratio constant) of 2 has the recurrence Sn=Sn-1 + Sn-1, where n stands for the index in the sequence S.
The Fibonacci sequence with a ratio constant of roughly 1.618 (known as Phi) has the recurrence Sn=Sn-1 + Sn-2.
The Narayana's Cows sequence (OEIS A000930) with a ratio constant of roughly 1.4656 (call it Moo or the bovine ratio) has the recurrence Sn=Sn-1 + Sn-3.
And so on.
(2^0)+1 = 2^(0+1)
(Phi^1)+1 = Phi^(1+1)
(Moo^2)+1 = Moo^(2+1)
Each of these equations simply shifts the bracket pairs along, so what's unique about the one featuring the golden ratio is that all the numerical values are 1's. Maybe that's what makes it beautiful.