Over the last week or so we have all become familiar with that bell-shaped curve that needs to be flattened to fall below the critical capacity of the NHS. Until the end of last week we were told that this could be achieved by mitigating the effects of the Covid-19 epidemic: no need to attempt the daunting task of eradicating it completely.

Render of the 2019-nCoV virion.

However, a study published yesterday, the same day the government announced more stringent measures than it indicated last week, throws a grim light on this idea. The study by the Imperial College Covid-19 Response Team finds mitigation strategies to be dangerously inadequate, likely to result in NHS capacity being overwhelmed eight times over and lead to at least 250,000 deaths in Great Britain. Instead, it says, we need to try and properly suppress the epidemic using a combination of measures that will need to remain in place for a very long time.

Perhaps surprisingly, given the length of time the virus has been wreaking havoc in other countries, the conclusion has only been reached in the last few days, based on experience in Italy and the UK and more detailed information about NHS capacity.

The results in short

The team behind the study considered two strategies we can try and take in the face of the disease. The first is suppression which aims to reverse the growth of the epidemic, reducing the number of cases to a very low number or even eradicating the disease completely, and keeping in that way. The second is mitigation, which only aims to slow the growth of the epidemic, easing pressure on health care systems, while protecting those at risk.

As far as mitigation is concerned, the team found that the optimal minimal combination of measures is home isolation of suspect cases, home quarantine for those living in the same household as suspect cases, and social distancing of the elderly and other people at high risk. This optimal combination of measures, so the results, might reduce peak health care demand by 2/3 and deaths by 1/2. This sounds good at first, but even the mitigated epidemic would lead to at least 250,000 deaths and overwhelm NHS peak capacity eight times over.

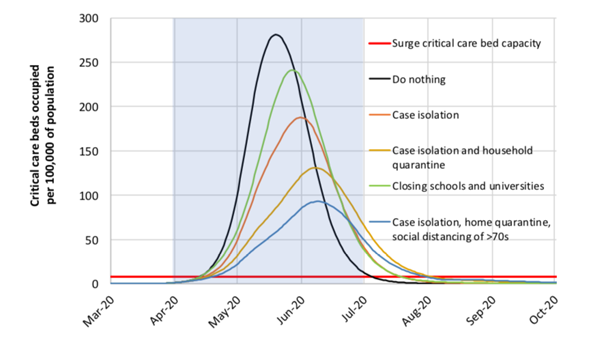
This graph shows mitigation strategy scenarios for GB showing critical care (ICU) bed requirements. The shaded region is the three-month period in which these interventions are assumed to remain in place. The graph is from the paper reporting the results of the new study.

If possible, the authors of the study conclude, countries who can still do so are better off trying to suppress the epidemic. Here the best combination of measures is more severe: isolation of infected people and quarantine for their families, social distancing of the entire population, and possibly also school and university closures (though the team point out that such closures may have a negative effect on the NHS as staff with children may not be able to come to work). The trouble with this suppression strategy is that measures will need to be kept in place until a vaccine becomes widely available — and this could take 18 months or more.

Banning mass gatherings is only predicted to have a relatively small effect because the time people spend in close contact at such gatherings is short compared to the contact people have at home, school or work.

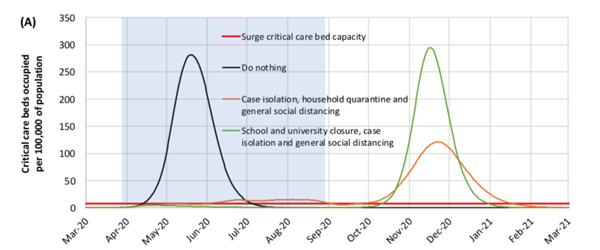
This graph shows suppression strategy scenarios for GB showing ICU bed requirements. The shaded region is the five-month period in which these interventions are assumed to remain in place. The graph is from the paper reporting the results of the new study.

Where do the predictions come from?

The team behind the study stress that there's a huge amount of uncertainty involved here. We are dealing with a new virus whose transmission still isn't fully understood. We also don't know exactly how people will respond to the various measures governments are taking or considering, and that the response may be different in different countries or even regions. In fact, even if governments didn't intervene at all, people might well decide to change their behaviour of their own accord. The authors of the study also stress that they didn't look into the ethical and economic impacts interventions might have, now or as knock-on effects later on — they simply focussed on feasibility and especially on the impact of interventions on health care systems.

The basis of the study is a mathematical model that can simulate the spread of a disease, which has already been used previously in studies of influenza. Loosely speaking, you can think of this a bit like a computer game which has a virtual population of individuals moving about their homes, work or school, and the wider community. The transmission of the disease can occur whenever an individual marked as infectious meets one marked as susceptible. In such epidemiological models the aim is to generate the make-up of a virtual population — the sizes and distributions, etc, of households, schools, workplaces — using as much real-life data as possible. The same goes for the all-important contact patterns between people, which heavily affect the rate of transmission. Data used for the latest study included information from the last Census, as well as data on class sizes and staff to student ratios, and reflected contact patterns that have been observed in studies of social mixing.

The characteristics of the disease we are looking at, Covid-19, are reflected in the model by various parameters. One of the most important numbers here is the reproduction number of the disease: the number of people an infected person goes on to infect on average. It's easy to see why this number is crucial. If the reproduction number is 1, and an infected person infects their victim within the first day of their disease, then every day will see just 1 new infection. If it is 2, however, then on day one we have 2 new infections, on day two 2x4=8 new infections, on day three 2x8=16, etc. The reproduction number describes just how steep the exponential growth involved in the spread of the disease is.

If we want to follow the strategy of suppressing the disease, then the aim should be to get the reproduction number to less than 1. If we're simply mitigating, we're only aiming to reduce it, but not necessarily to below 1. For their study the Covid-19 reproduction number was assumed to be 2.4, but values between 2.0 and 2.6 were also examined.

Other important parameters are the incubation period of the disease (assumed to be 5.1 days) and the amount of time someone is infectious for. As with the reproduction number, the team estimated values for these parameters and their variability based on available data. They also assumed, using data from China as evidence, that once a person has had the disease, they are immune at least in the short term. (For more details on the model and its parameters and assumptions, see the original paper.)

To start the model off, the team "seeded" the infection in each country at an exponentially growing rate, with a doubling of cases every 5 days, from early January 2020. To make things as realistic as possible, this seeding was calibrated so that the epidemics that emerged in the model reproduced the observed number of deaths in Great Britain or the US seen by 14th March 2020.

With the model in place, the team then tested the effect of five different interventions:

• Case isolation: People with the disease isolate at home for seven days,
• Voluntary home quarantine: once someone has symptoms of the disease, all household members remain at home for 14 days,
• Social distancing of those over 70 years of age,
• Social distancing of the entire population,
• Closure of schools and universities.

When looking at the mitigation strategy, the team assumed that the intervention would mostly remain in place for three months, apart from social distancing for over-70s, which would remain in place for four months. For the suppression strategy they assumed interventions to remain in place five months or longer.

Each intervention, or combination of interventions, results in a change of contact rates. For example, the study assumes that social distancing of the entire population results in all households reducing their contacts outside the home, school or workplace by 75%. School contact rates remain unchanged, workplace contact rates reduce by 25%, but household contact rates increase by 25%. These changed contact rates can be reflected in the parameters of the model, and then result in a different evolution of the model epidemic. This, in a nutshell (and ignoring a lot of detail of the modelling process), is what the predictions of how fast and wide Covid-19 will spread under different interventions are based on.

NHS stress

One aim of the study was to see how the pandemic will impact on the NHS. To predict this impact, the team used data from Italy and China, as well as early data from the UK.

For example, adjusting data from China for the UK population led the team to assume an infection to fatality ratio of 0.9% with 4.4% of infected people needing to be hospitalised. Based on early reports from the UK, Italy and China, they assumed that 30% of all hospitalised cases will need critical care, such as invasive mechanical ventilation. Of those that do need critical care 50% are assumed to die. The team calculated the demand for beds assuming that patients stay in hospital for eight days if they don't need critical care, and for 16 days if they do.

The results in more detail

The most significant result of the study, as already mentioned above, is that mitigation alone isn't good enough: we need to try and suppress the disease instead. The optimal minimal combination of interventions to try and bring the all-important reproduction number below 1 is social distancing of the entire population, case isolation and either school and university closures or household quarantine. All four of these interventions together are most likely to ensure that the demand on critical care beds remains within capacity (assuming that school closures don't affect NHS staff so badly that their effect is cancelled out).

When it comes to the length of time the interventions need to remain in place, we face the threat of a second hump to the bell curve. Once the rules are relaxed, more people may become infected again and this may lead to a second epidemic later on. Here, the much-discussed phenomenon of herd immunity comes into play too: the more successful an intervention is at temporarily suppressing the disease, the fewer people become infected and hence immune, and the worse the second epidemic will turn out to be. To be sure the suppression strategy will really work, the study suggests, we need to keep interventions in place until large quantities of a vaccine are available. And this could be eighteen months or more.

Given these grim prospects the team also investigated the idea that interventions, rather than being imposed for some fixed amount of time, can be switched on or off in response to certain triggers — for example when confirmed infections in intensive care units fall above (on) or below (off) a critical number. This appears to be a good idea in general, especially because triggers can take account of regional variations in of the epidemic: what is good for London at a particular moment in time may not be necessary in Scotland. But whichever way you look at it, according to the study, we are in for the long haul.

The authors point out that their drastic conclusions were only reached within the last few days, as better estimates on the demand of intensive care units became available — previous estimates had assumed only half the demand. This late turn-around has drawn criticism from some quarters (which we will report more on once we have the information).

The one thing that is really certain is that there's a lot of uncertainty surrounding all the predictions. As the authors gloomily point out, "it is not at all certain that suppression will succeed long term; no public health intervention with such disruptive effects on society has been previously attempted for such a long duration of time. How populations and societies will respond remains unclear."

But who knows — maybe the uncertainties will play out in our favour for once, and things will not turn out as bad as it currently seems they will. We can only hope.