On Friday the 13th, in April 2029, the asteroid Apophis will pass close enough to the Earth to be viewed with the naked eye. This will be an exciting event for stargazers, but for a short time in 2004 there was concern that this event would be cataclysmic. In December 2004 Apophis, named after the Egyptian serpent god who brings darkness to the Earth, was given a 1 in 37 chance of impacting with the Earth based on initial observations of the asteroid's orbit. Luckily, additional observations showed that the asteroid would just be a near miss in 2029, though there is still a slim chance of a collision during a pass in 2036.
While you breathe a sigh of relief, some people are already making plans for how to deal with any potential armageddons in the future. One such person is David French, a PhD student in aerospace engineering at North Carolina State University, who has worked out how to stop asteroids from colliding with the Earth by attaching a massive ball and chain (a large ballast mass connected by a long tether). By attaching the ballast, French explains, "you change the object's center of mass, effectively changing the object's orbit and allowing it to pass by the Earth, rather than impacting it."
Does this all sound a bit far-fetched, and like some movie Bruce Willis or Tea Leoni should be starring in? NASA's Near Earth Object Program has identified more than 1,000 "potentially hazardous asteroids" and they are finding more all the time. "While none of these objects is currently projected to hit Earth in the near future, slight changes in the orbits of these bodies, which could be caused by the gravitational pull of other objects, push from the solar wind, or some other effect, could cause an intersection," French explains.
So French, and Andre Mazzoleni,NC State Associate Professor of Mechanical and Aerospace Engineering, studied whether an asteroid-tether-ballast system could effectively alter the motion of an asteroid to ensure that it misses the Earth. And encouragingly the answer seems to be: yes, it can.
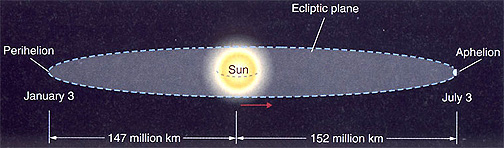
The elliptical orbit of the Earth (shown almost side on in this image) has a closest pass
to the Sun at the perihelion and a furthest pass at the aphelion [Image courtesy NASA]
Kepler discovered in the 17th century that all the planets, as they move around the Sun, trace a path that is shaped like a squashed circle, an ellipse. An ellipse has two foci, and is definied by its greatest width, called the major axis, and eccentricity, a measure of how squashed the shape is. A circle has zero eccentricity, while a very squashed ellipse has eccentricity close to one. For an orbiting body the Sun is located at one of these two foci. The Earth travels on an orbit that is quite close to circular — it has eccentricity of 0.0167 and a semimajor (half the major axis) of 149,597,887.5 km (which is the definition of 1 astronomical unit or AU). The distance between the Earth and the Sun varies from around 147 million to 152 million kilometres.
Asteroids also move in elliptical orbits and most known asteroids move in a band between the orbits of Mars and Jupiter. However, they are defined as Near Earth if their closest pass to the Sun, at a point on their elliptical orbit called the perihelion, is less than 1.3 AU (so the asteroid passes the Sun a third further out than the Earth), and as potentially hazardous if they pass within 0.05 AU of Earth's orbit (which is about twice the distance from the Earth to the Moon).
Mathematics of an ellipse
An ellipse, which looks like a squashed circle, is uniquely described by the semimajor axis 
(half the width) and the semiminor axis 
(half the height).
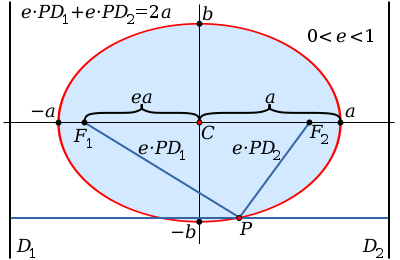
If the centre of the ellipse is placed on the origin, you can describe it by the equation
![\[ \frac{x^2}{a^2} + \frac{y^2}{b^2}=1 \]](/MI/428749478337fefe5a4d50243cad0e48/images/img-0001.png) |
An ellipse has two points on the major axis called the foci, such that the sum of distances from each focus to any point on the ellipse is equal to 
.
The eccentricity, 
, of an ellipse is the amount it differs from a circle (which has an eccentricity of 0). Mathematically it is defined as the ratio of the distance between the foci (say 
) and the length of the major axis, 
.
![\[ e=\frac{2d}{2a} \]](/MI/d40fd76e539a9e69b1cd91cbb1043ade/images/img-0004.png) |
.
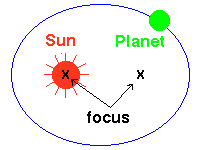
The Sun is at one of the foci of the elliptical orbit [Image courtesy NASA]
The Sun is at one of the foci of an elliptical orbit, so for simplicity let's put the Sun at the origin, and have the semimajor axis of the orbit lying along the 
-axis. Then we can describe the orbit using the equation
![\[ R=\frac{a(1-e^2)}{1+e \cos \theta } \]](/MI/252facb265bcc1fa8f8e7c807e816cf0/images/img-0002.png) |
is the distance from the sun and 
is the angle from the -axis.
The point 
corresponds to the aphelion, the furthest point from the sun at a distance of
![\[ \frac{a(1-e^2)}{1-e}=a+ae. \]](/MI/7c5279ddd53a05ec405170c98064dc3d/images/img-0002.png) |
the orbiting body is at a distance of 
, which you can work out to be 
. The point 
corresponds to the perihelion, the closest point to the sun at a distance of 
French and Mazzoleni studied how the elliptical orbits of these hypothetical asteroids would be affected over the 20 years before any impact by attaching a mass to the asteroid via a long tether. This has an effect of changing the centre of mass of the asteroid, effectively moving the asteroid to another orbit. Their goal was to divert the trajectory of the an Earth-bound asteroid by one Earth radius, a goal set out in NASA's report to US Congress on how to deal with such a situation.
Using NASA's database of potentially hazardous asteroids (PHAs) as examples, they solved the equations of motion for hypothetical Earth-bound versions. They tried many cases to determine the effect of the parameters involved, such as the size of the orbit (semimajor axis), the shape (eccentricity), the tether length (which ranged from 100 to 100,000 km), the ratio of the ballast mass to the asteroid mass (ballasts from one tenth to one millionth the mass of the asteroid), as well as the initial position of the ballast with repect to the asteroid.
French and Mazzoleni found that the system was most effective for smaller asteroids, with smaller and more eccentric (squashed) orbits. But by comparing their results for data for known PHAs, they showed that many similar asteroids could be diverted with tethers of 10,000km, and over half could be diverted with the longest tethers of 100,000km. (The maximum length of 100,000km was taken from other scientific studies of the use of tether systems in space, such as the space elevator.)"It's hard to imagine the scale of both the problem and the potential solutions," French says. "The Earth has been hit by objects from space many times before, so we know how bad the effects could be. For example, about 65 million years ago, a very large asteroid is thought to have hit the Earth in the southern Gulf of Mexico, wiping out the dinosaurs, and, in 1907, a very small airburst of a comet over Siberia flattened a forest over an area equal in size to New York City. The scale of our solution is similarly hard to imagine.
"Using a tether somewhere between 1,000 kilometers (roughly the North-South length of the UK) to 100,000 kilometers (which would wrap around the Earth two and a half times) to divert an asteroid sounds extreme. But compare it to other schemes," French says. "They are all pretty far out. Other schemes include: a call for painting the asteroids in order to alter how light may influence their orbit; a plan that would guide a second asteroid into the threatening one; and of course, there are nukes. Nuclear weapons are an intriguing possibility, but have considerable political and technical obstacles. Would the rest of the world trust [the US] to nuke an asteroid? Would we trust anyone else? And would the asteroid break into multiple asteroids, giving us more problems to solve?"
There is still a lot of work to be done before we could consider sending astronauts up with a very big coil of rope. At the moment the analysis is simplified and doesn't take into account the rotation of the asteroid, or how the tether would be connected to the asteroid. French says that although some of these questions are challenging, they have some ideas how they could be tackled. "We haven't answered all the questions that would arise in the course of implementing this technique. But, having established this concept as viable, we invite the broader scientific community to help us solve such problems."
Further reading
You can read more about ellipses, asteroids and astronomy in Plus:
Comments
minor correction to equation for orbit
Should it be R=a(1-e^2)/(1-ecos(theta))?
Otherwise, great article.