
The life and numbers of Fibonacci
Fibonacci is one of the most famous names in mathematics. This would come as a surprise to Leonardo Pisano, the mathematician we now know by that name. And he might have been equally surprised that he has been immortalised in the famous sequence – 0, 1, 1, 2, 3, 5, 8, 13, ... – rather than for what is considered his far greater mathematical achievement – helping to popularise our modern number system in the Latin-speaking world.
The Roman Empire left Europe with the Roman numeral system which we still see, amongst other places, in the copyright notices after films and TV programmes (2013 is MMXIII). The Roman numerals were not displaced until the mid 13th Century AD, and Leonardo Pisano's book, Liber Abaci (which means "The Book of Calculations"), was one of the first Western books to describe their eventual replacement.

Leonardo Fibonacci c1175-1250.
Leonardo Pisano was born late in the twelfth century in Pisa, Italy: Pisano in Italian indicated that he was from Pisa, in the same way Mancunian indicates that I am from Manchester. His father was a merchant called Guglielmo Bonaccio and it's because of his father's name that Leonardo Pisano became known as Fibonacci. Centuries later, when scholars were studying the hand written copies of Liber Abaci (as it was published before printing was invented), they misinterpreted part of the title – "filius Bonacci" meaning "son of Bonaccio" – as his surname, and Fibonacci was born.
Fibonacci (as we'll carry on calling him) spent his childhood in North Africa where his father was a customs officer. He was educated by the Moors and travelled widely in Barbary (Algeria), and was later sent on business trips to Egypt, Syria, Greece, Sicily and Provence. In 1200 he returned to Pisa and used the knowledge he had gained on his travels to write Liber Abaci (published in 1202) in which he introduced the Latin-speaking world to the decimal number system. The first chapter of Part 1 begins:
"These are the nine figures of the Indians: 9 8 7 6 5 4 3 2 1. With these nine figures, and with this sign 0 which in Arabic is called zephirum, any number can be written, as will be demonstrated."
Italy at the time was made up of small independent towns and regions and this led to use of many kinds of weights and money systems. Merchants had to convert from one to another whenever they traded between these systems. Fibonacci wrote Liber Abaci for these merchants, filled with practical problems and worked examples demonstrating how simply commercial and mathematical calculations could be done with this new number system compared to the unwieldy Roman numerals. The impact of Fibonacci's book as the beginning of the spread of decimal numbers was his greatest mathematical achievement. However, Fibonacci is better remembered for a certain sequence of numbers that appeared as an example in Liber Abaci.

A page of Fibonacci's Liber Abaci from the Biblioteca Nazionale di Firenze showing the Fibonacci sequence (in the box on the right)."
The problem with rabbits
One of the mathematical problems Fibonacci investigated in Liber Abaci was about how fast rabbits could breed in ideal circumstances. Suppose a newly-born pair of rabbits, one male, one female, are put in a field. Rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits. Suppose that our rabbits never die and that the female always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was... How many pairs will there be in one year?
- At the end of the first month, they mate, but there is still only 1 pair.
- At the end of the second month the female produces a new pair, so now there are 2 pairs of rabbits.
- At the end of the third month, the original female produces a second pair, making 3 pairs in all.
- At the end of the fourth month, the original female has produced yet another new pair, the female born two months ago produced her first pair also, making 5 pairs.
Now imagine that there are $x_n$ pairs of rabbits after $n$ months. The number of pairs in month $n+1$ will be $x_n$ (in this problem, rabbits never die) plus the number of new pairs born. But new pairs are only born to pairs at least 1 month old, so there will be $x_{n-1}$ new pairs. So we have $$ x_{n+1} = x_n + x_{n-1} $$ which is simply the rule for generating the Fibonacci numbers: add the last two to get the next. Following this through you'll find that after 12 months (or 1 year), there will be 233 pairs of rabbits.
Bees are better
The rabbit problem is obviously very contrived, but the Fibonacci sequence does occur in real populations. Honeybees provide an example. In a colony of honeybees there is one special female called the queen. The other females are worker bees who, unlike the queen bee, produce no eggs. The male bees do no work and are called drone bees.
Males are produced by the queen's unfertilised eggs, so male bees only have a mother but no father. All the females are produced when the queen has mated with a male and so have two parents. Females usually end up as worker bees but some are fed with a special substance called royal jelly which makes them grow into queens ready to go off to start a new colony when the bees form a swarm and leave their home (a hive) in search of a place to build a new nest. So female bees have two parents, a male and a female whereas male bees have just one parent, a female.
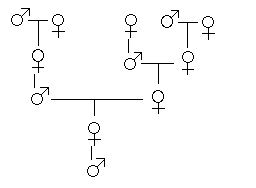
Let's look at the family tree of a male drone bee.
He has 1 parent, a female.
He has 2 grandparents, since his mother had two parents, a male and a female.
He has 3 great-grandparents: his grandmother had two parents but his grandfather had only one.
How many great-great-grandparents did he have?
Again we see the Fibonacci numbers :
| Number of | parents | grandparents | great- grandparents | great-great- grandparents | great-great-great- grandparents |
| of a MALE bee | 1 | 2 | 3 | 5 | 8 |
| of a FEMALE bee | 2 | 3 | 5 | 8 | 13 |
Spirals and shells

Bee populations aren't the only place in nature where Fibonacci numbers occur, they also appear in the beautiful shapes of shells. To see this, let's build up a picture starting with two small squares of size 1 next to each other. On top of both of these draw a square of size 2 (=1+1). We can now draw a new square – touching both one of the unit squares and the latest square of side 2 – so having sides 3 units long; and then another touching both the 2-square and the 3-square (which has sides of 5 units). We can continue adding squares around the picture, each new square having a side which is as long as the sum of the latest two square's sides. This set of rectangles whose sides are two successive Fibonacci numbers in length and which are composed of squares with sides which are Fibonacci numbers, we will call the Fibonacci Rectangles.
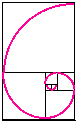
If we now draw a quarter of a circle in each square, we can build up a sort of spiral. The spiral is not a true mathematical spiral (since it is made up of fragments which are parts of circles and does not go on getting smaller and smaller) but it is a good approximation to a kind of spiral that does appear often in nature. Such spirals (called logarithmic spirals) are seen in the shape of shells of snails and sea shells. The image below of a cross-section of a nautilus shell shows the spiral curve of the shell and the internal chambers that the animal using it adds on as it grows. The chambers provide buoyancy in the water.

Fibonacci numbers also appear in plants and flowers. Some plants branch in such a way that they always have a Fibonacci number of growing points. Flowers often have a Fibonacci number of petals, daisies can have 34, 55 or even as many as 89 petals!
A particularly beautiful appearance of fibonacci numbers is in the spirals of seeds in a seed head. The next time you see a sunflower, look at the arrangements of the seeds at its centre. They appear to be spiralling outwards both to the left and the right.
 |
 |
 |
At the edge of this picture of a sunflower, if you count those curves of seeds spiralling to the left as you go outwards, there are 55 spirals. At the same point there are 34 spirals of seeds spiralling to the right. A little further towards the centre and you can count 34 spirals to the left and 21 spirals to the right. The pair of numbers (counting spirals curving left and curving right) are (almost always) neighbours in the Fibonacci series.
The same happens in many seed and flower heads in nature. The reason seems to be that this arrangement forms an optimal packing of the seeds so that, no matter how large the seed head, they are uniformly packed at any stage, all the seeds being the same size, no crowding in the centre and not too sparse at the edges.
Nature seems to use the same pattern to arrange petals around the edge of a flower and to place leaves round a stem. What is more, all of these maintain their efficiency as the plant continues to grow and that's a lot to ask of a single process! So just how do plants grow to maintain this optimality of design?
Golden growth
Botanists have shown that plants grow from a single tiny group of cells right at the tip of any growing plant, called the meristem. There is a separate meristem at the end of each branch or twig where new cells are formed. Once formed, they grow in size, but new cells are only formed at such growing points. Cells earlier down the stem expand and so the growing point rises. Also, these cells grow in a spiral fashion: it's as if the meristem turns by an angle, produces a new cell, turns again by the same angle, produces a new cell, and so on. These cells may then become a seed, a new leaf, a new branch, or perhaps on a flower become petals and stamens.

The leaves here are numbered in turn – each is exactly 0.618 of a clockwise turn (222.5°) from the previous one.
The amazing thing is that a single fixed angle of rotation can produce the optimal design no matter how big the plant grows. The principle that a single angle produces uniform packings no matter how much growth appears was suspected as early as last century but only proved mathematically in 1993 by Stéphane Douady and Yves Couder, two French mathematicians. Making 0.618 of a turn before producing a new seed (or leaf, petal, etc) produces the optimal packing of seeds no matter the size of the seed head. But where does this magic number 0.618 come from?
The golden ratio
If we take the ratio of two successive numbers in Fibonacci's series, dividing each by the number before it, we will find the following series of numbers:
1/1 = 1, 2/1 = 2, 3/2 = 1.5, 5/3 = 1.666..., 8/5 = 1.6, 13/8 = 1.625, 21/13 = 1.61538...
If you plot a graph of these values you'll see that they seem to be tending to a limit, which we call the golden ratio (also known as the golden number and golden section).
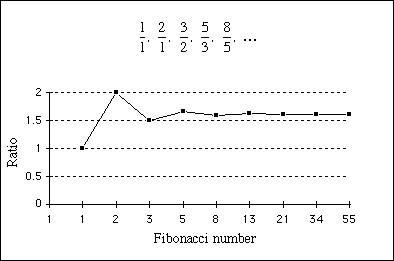
Ratio of successive Fibonacci terms.
It has a value of $(\sqrt 5 + 1)/2$ ( approximately 1.618034) and is often represented by a Greek letter Phi, written as $\Phi$. The closely related value which we write as $\phi$, a lowercase phi, is just the decimal part of Phi, namely 0.618034... ($(\sqrt 5 - 1)/2$), the number that accounts for the spirals in the seedheads and the arrangements of leaves in many plants. But why do we see phi in so many plants?
The number Phi (1.618034...), and therefore also phi (0.618034...), are irrational numbers: they can't be written as a simple fraction. Let's see what would happen if the meristem in a seed head instead turned by some simpler number, for example the fraction 1/2. After two turns through half of a circle we would be back to where the first seed was produced. Over time, turning by half a turn between seeds would produce a seed head with two arms radiating from a central point, leaving lots of wasted space.
|
A seed head produced by 0.5=1/2 turns between seeds: alternate seeds line up. |
 A seed head produced by 0.48=12/25 turns between seeds: the seeds form two revolving arms. |
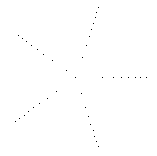 A seed head produced by 0.6=3/5 turns between seeds: the seeds form 5 straight arms. |

Pi turns between seeds produces seven spiralling arms
Something similar happens for any other simple fraction of a turn: seeds grow in spiral arms that leave a lot of space between them (the number of arms is the denominator of the fraction). So the best value for the turns between seeds will be an irrational number. But not just any irrational number will do. For example, the seed head created with pi turns per seed seems to have seven spiralling arms of seeds. This is because 22/7 is a very good rational approximation of pi.
What is needed in order not to waste space is an irrational number that is not well approximated by a rational number. And it turns out that Phi (1.618034...) and its decimal part phi (0.618034...) are the "most irrational" of all irrational numbers. (You can find out why in Chaos in number land: the secret life of continued fractions.) This is why a turn of Phi gives the optimal packing of seeds and leaves in plants. It also explains why the Fibonacci numbers appear in the leaf arrangements and as the number of spirals in seedheads. Adjacent Fibonacci numbers give the best approximations of the golden ratio. They take turns at being the denominator of the approximations and define the number or spirals as the seed heads increase in size.
How did so many plants discover this beautiful and useful number, Phi? Obviously not from solving the maths as Fibonacci did. Instead we assume that, just as the ratio of successive Fibonacci numbers eventually settles on the golden ratio, evolution gradually settled on the right number too. The legacy of Leonardo Pisano, aka Fibonacci, lies in the heart of every flower, as well as in the heart of our number system.
Further Reading
If you have enjoyed this article you might like to visit Fibonacci Numbers and the Golden Section.
About this article

This article is based on material written by Dr R. Knott, who was previously a lecturer in the Department of Computing Studies at the University of Surrey. Knott started the website on Fibonacci Numbers and the Golden Section back in 1996 as an experiment at using the web to inspire and encourage more maths investigations both inside and outside of school time. It has since grown and now covers many other subjects, all with interactive elements and online calculators. Although now retired, Knott still maintains and extends the web pages. He is currently a Visiting Fellow at the University of Surrey and gives talks all over the country to schools, universities, conferences and maths societies. He also likes walking, mathematical recreations, growing things to eat and cooking them.
Comments
Anonymous
Very interesting stuff thank you
Anonymous
Interesting, indeed! Now I know where the producers of the iq tests got their number series questions.
Anonymous
Its in fact the golden mean sequence used in sacred geometry. Phi is what Fibonacci used to make the mathmatical formula. He didn't invent the pattern itself. That was brought here. This pattern will be above us cosmicly to view in 2012.
Anonymous
Please tell more- what do you mean above us? Exactl;y when will this occur? I love this stuff!
Anonymous
Ive got a maths homework to research famous mathmaticians and do a presentation on one and I chose fibonacci . this has really helped me thanks a lot
Anonymous
So when did we see this pattern, it's 2013 now and i didn't hear anything about this??
Jane @ Arraial d'Ajuda
Anonymous
Thank you. This was the most complete report I have read on the Fibonacci. I needed this.
Anonymous
Creating the code for secret messages to-day, how would it look like using the Fibonacci sequence and the encryption at Kryptos (CIA) super imposed on a Mobius circle? Any one, who comes up with a solution will be acknowledged in my new novel Thanks.
Anonymous
SIR
My name is saksham goyal from india. we could code like this:
1st letter a as 3rd fibonacci term 1
2nd letter b as 4th fibonacci term 2
for spaces we can use 0
for very long number such as 75025 (26th for z) we can use 7+5+0+2+5 = 19
in case for same sums like 75025 and 2584(18th) we can either right full number or write 19 to base 18 or to base 26(i.e. in sub script)
in case you like this..............plz email me on sakshamgoyal06@yahoo.com
Anonymous
well worth thinking. Indeed it crossed from my mind when I was composing a short story.ı would say non verbal signals such as musical tones would be my choice and a good ear training of course.
good luck.
Anonymous
I knew about "The Golden ratio" before but never understand how and why this is applicable in "Fibonacci Sequence"...
Thanks a lot for your explanation... . Also nature loves Mathematics and it is again proved by your example.
Anonymous
this helped me understand more about Fibonacci and his sequence of numbers for my report on him.. thanks :)
Anonymous
for those that think the Fibonacci number(Fn) sequence is just a coincidence there are MANY"non" math equations and sums on the "insides".For example by combining 3 consecutive Fn creates a new Hybrid Fibonacci number that still sums in a sequence!!...btw...a "0"* is added where needed.
ex 0,1,1,2,3,5,8 become
011,112,123,235,358 etc
011+112=123
112+123=235
123+235=358
20305+30508=50813*
30508+50813=81321*
5813 +81321=132134
81321+132134=213455
132134+213455=345589
21034055+34055089=55089144*
this works forwards and backwards. It also works with the "sister" Lucas numbers(Ln)sequence and of course adding 2 hybrid Fn equals a hybrid Ln and all it's variations......and yes ....they still sum to the golden ratio!!.The Fn are the most unique sequence there is.IMO it is the key to everything.
Anonymous
Hi, I like to study Fibonacci numbers and would like to ask you more about this comment, if you don't mind....pls contact me
linelites 'at' gmail.com
thanks
Anonymous
Your site was a saviour to me and my project partner we had researched about why Fibonacci had formed this sort of formula. Thanks A Lot
Anonymous
You know who else is your savior? the author of this article.
Anonymous
Fibonacci sequence is interesting.
For fun and learning, I did some c++ codes for it here: http://cppstudent.blogspot.com/2013/09/fibonacci-using-recursion.html
Anonymous
Fibonacci also described the method of "casting out the nines" (to check the accuracy of arithmetical calculations) in his book "Liber Abaci" in 1202. See
http://www.significancemagazine.org/details/webexclusive/1382001/One-sm…
Anonymous
What are the 2 major works of Fibonacci?
Anonymous
Hello,
It has been already seen that the Fibonacci sequence or Golden ratio appears in the Nature as we can see in many examples.
However, I would like to know if there is an explanation why this specific number appears ? Is there any plausible mathematical explanation to it ? Why nature chosen this constant number ?
Thanks.
Anonymous
Actually there is. If you go on youtube and search up Vi Hart, go and watch her videos on Fibonacci and plants. But basically plants have a hormone that tells them to grow and they grow away from each other if you look at the picture i the article above you can see that happen. And It just so happens that it happens in fibonacci numbers. Vi Hart's videos will explain it in more depth.
Hope this helps!
Marianne
The explanation is in the last paragraphs of this article. It is connected to the irrationality of phi.
Anonymous
What was the kind of number system Europe used before Fibonacci introduced the new number system
Anonymous
It was the Roman Numeral System which was very messy when doing long calculations
roy
A true romantic discourese on Fibinacci numbers, excellent.
Anynonymus
This was extremely helpful thanks!!!!
Bedazzle
How was the mathematical rule for the Fibonacci patter was derived?
Stephen Bartels
In this paragraph:
"Now imagine that there are $x_ n$ pairs of rabbits after $n$ months. The number of pairs in month $n+1$ will be $x_ n$ (in this problem, rabbits never die) plus the number of new pairs born. But new pairs are only born to pairs at least 1 month old, so there will be $x_{n-1}$ new pairs."
You say that new pairs are only born to pairs at least 1 month old but is this correct? Earlier you state that pairs can mate at 1 month but only produce new pairs at 2 months. Therefor new pairs are only born to pairs at least 2 months old (not 1 month old). If this is so, how does it affect your formula?
Thanks
Anonymous
He actually mentions this and takes it into his calculations.
ALAA
Hi, I think that I discovered a new sequence related to Fibonacci sequence:
You might knew that the Fibonacci sequence starts with 0 and 1 and the following number is the sum of the previous 2; every time you go further in the sequence, the ratio of two consecutive numbers be nearer to the golden ratio (phi). But you can start with any two numbers not only 0 and 1 for example (2, 6; 490, 10; 56, 56...etc.) or two similar numbers and the ratio of two consecutive numbers is also the golden ratio. If we think deeper, we can start with phi and phi as the first two numbers and the ratio of two consecutive numbers (if you choose them far away from the beginning) is also approximately phi. But if you look on the numbers of this sequence, an amazing pattern appear. The first 4 or 5 numbers are ordinary but the 5th or 6th numbers are the beginning of the pattern. The digits after the decimal point of these numbers is as following:
0,9,0,9,0,99,00,99,00,99,000,999,000… and so on!!!
matus hromec
one of the best articles that i ever read
Rajan L
Hi can you explain Fibonacci Retracements and how they work?
Liam Morris
In reply to the man's question 10/18, about Fibonacci retracement, this is an expression in the investment industry referring to the % of a recent movement in an investment's market price that is 'retraced' after a recognized reversal in the security's price. Technical analysts within the investment management world use the Fibonacci ratio, and variations, to aid in forecasting the probability of the 'next turn' in the dynamic market price of a specified security or market index. It is only one of many types of calculations and geometric observations investment analysts use in forecasting 'probable' turning points (or reversals) in investment prices.
For example, if stock A's recent price movement was downward by $10, before it turned, or bounced, then the 'retracement' of the $10 is what is monitored with Fibonacci ratios to determine the next possible reversal of the stock price. In this example, if one utilizes the most popular Fibonacci ratio of .618, then the retracement of the $10 in our example might be be $6.18, the amount the security's price may advance before reversing again, as in a stair step formation. As most people are aware, stock market prices don't go straight up or down over time; they go up and down in a stair-step fashion, and it's the Fibonacci ratios that help analysts determine these possible change in the current trend.
In the real world, investments don't turn on the Fibonacci-calculated pricing, but they do seem to turn at certain variations of the Fibonacci ratios, ie, the square root of .618, or Fib squared, or even the reciprocal of Fib compared to 1, ie, .382 (1- .618). None of the various Fib ratios do not guarantee a turning point in a stock's price, but they identify possible pricing points, that wouldn't exist otherwise. It's not certain when the Leonardo's famous ratio started to be utilized in the investment industry, but that would be something to investigate.
Liam Morris
Fib Fan
V.S.Gopalakrishnan
Actually Fibonacci number was nothing original. When he was in North Africa, he studied translated ancient Indian mathematical books from which he learnt the concept. After he went back to Italy, Europe called the numbers Fibonacci numbers.
Timothy Dodge McCollum
No surprise. But Arabic written documents usually show a source. Any ideas?
Jacob van Pareen
Thanks for a very logical explanation, especially the family tree of a bee!
I had it all wrong on the golden ratio!
David Salusbury
Great piece Doc Knott!
Did you know of the Fib sequence resulting from a frog doing long or short jumps on stepping stones?
This is much more comprehensible than the flower and other natural (but tough to demonstrate) applications.
DS, Ottawa
Anon
Thank you, I had a project of Fibonacci and this helped a ton.
Gerson Tabosa
Adorei esse artigo, muito interessante para mostrar a Matemática aos nossos alunos ,principalmente ,poder expressar um fórmula para a série de Fibonacci. Grato