Life on the beach with Markov chains

Markov chains are exceptionally useful tools for calculating probabilities and are used in fields such as economics, biology, gambling, computing (such as Google's search algorithm), marketing and many more. They can be used when the probability of a future event is only dependent on a current event. The Russian mathematician Andrei Markov was the first to work in this field (in the late 1800s).

Beach life

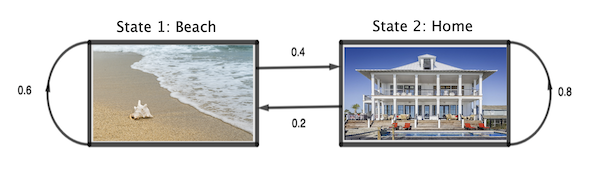
A Markov chain between home and the beach

The picture above is an example of a situation which can be modelled using a Markov chain. We have two states: Beach (state 1) and Home (state 2). In our happy life we spend all the hours of the day in either one of these two states. If we are on the beach then the probability we still remain on the beach in one hour is 0.6 and the probability we go home in one hour is 0.4. If we are at home the probability we remain at home in one hour is 0.8 and the probability we go to the beach is 0.2.

First we need to represent our information in a matrix form. A general 2×2 matrix is written as

$A = \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right)$

Where the subscript tells you the row and column (e.g. $a_{12}$ tells you it is in the first row and 2nd column).

For our Markov chain we define the following matrix:

$M = \left( \begin{array}{cc} p(m_{11}) & p(m_{12}) \\ p(m_{21}) & p(m_{22}) \end{array} \right).$

Here $m_{11}$ is the situation of starting in state 1 and staying in state 1. And $m_{12}$ is the situation of starting in state 1 and moving to state 2. The value $p(m_{12})$ is the probability of starting in state 1 and moving to state 2. So for our beach existence we have:

$M = \left( \begin{array}{cc} 0.6 & 0.4 \\ 0.2 & 0.8 \end{array} \right).$

The 0.6 shows that if we are already on the beach we have a 0.6 chance of still being on the beach in one hour.

Where will we be in the future?

For someone starting on the beach, the probability they'll be on the beach in two hours is the probability they stay on the beach that whole time, $p(m_{11})p(m_{11})$ , plus the probability that they go home and then come back to the beach, $p(m_{12})p(m_{21})$ . Here we see the benefit of Markov chains in that they allow us to utilise computer power to now calculate where someone will be in the future – simply by taking the power of the matrix. To find the all the probabilities after two hours I can square my matrix:

$M^2 = \left( \begin{array}{cc} p(m_{11}) & p(m_{12}) \\ p(m_{21}) & p(m_{22}) \end{array} \right) \left( \begin{array}{cc} p(m_{11}) & p(m_{12}) \\ p(m_{21}) & p(m_{22}) \end{array} \right).$

Using the rules of matrix multiplication this then gives:

$M^2 = \left( \begin{array}{cc} p(m_{11})p(m_{11})+p(m_{12})p(m_{21}) & p(m_{11})p(m_{12})+p(m_{12})p(m_{22}) \\ p(m_{21})p(m_{11})+p(m_{22})p(m_{21}) & p(m_{21})p(m_{12})+p(m_{22})p(m_{22}) \end{array} \right).$

Here, in the top left entry, you'll recognise our probability of someone starting on the beach and being on the beach in two hours. We'll use arrow notation to represent the start and end state, so $p(m_{1\rightarrow 1})$ means starting at state 1 (the beach) and ending at state 1 after two hours. We can then calculate all the probabilities as:

$M^2 = \left( \begin{array}{cc} p(m_{1\rightarrow 1}) & p(m_{1\rightarrow 2}) \\ p(m_{2\rightarrow 1}) & p(m_{2\rightarrow 2}) \end{array} \right) = \left( \begin{array}{cc} 0.44 & 0.56 \\ 0.28 & 0.72 \end{array} \right).$

We can see that for someone who started in the beach, the chance of them being on the beach in two hours is 0.44. Equally the probability of someone who started in the house being on the beach in two hours is 0.28.

I can then carry on with matrix multiplication to work out where someone will likely be for any given number of hours in the future:

$M^ n = \left( \begin{array}{cc} p(m_{1\rightarrow 1}) & p(m_{1\rightarrow 2}) \\ p(m_{2\rightarrow 1}) & p(m_{2\rightarrow 2}) \end{array} \right)$

where now $p(m_{1 \rightarrow 1})$ means starting at state 1 and ending at state 1 after $n$ hours. So, for example, if I want to see where someone will be in 24 hours I simply do the matrix multiplications to get:

$M^{24} = \left( \begin{array}{cc} p(m_{1\rightarrow 1}) & p(m_{1\rightarrow 2}) \\ p(m_{2\rightarrow 1}) & p(m_{2\rightarrow 2}) \end{array} \right) = \left( \begin{array}{cc} 0.333 & 0.667 \\ 0.333 & 0.667 \end{array} \right).$

We can see that now it doesn't actually matter (to three significant figures anyway) where someone started – if they started on the beach there is a 0.333 chance they are on the beach in 24 hours, if they started in the house there is also a 0.333 chance they are on the beach in 24 hours. So I can conclude that as the number of hours increase towards infinity that the person in this scenario would spend 1/3 of their time on the beach and 2/3 of their time at home – not a bad life!

A more demanding beach life

A Markov chain between home, scuba and the beach

We can see that things get much more complicated, even by adding just one extra state. Now we have 3 possible states: Beach (state 1), Home (state 2) and SCUBA (state 3). This time we need a 3×3 matrix:

$M = \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right)$

and as before we define our probability matrix for our example as:

$M = \left( \begin{array}{ccc} 0.6 & 0.1 & 0.3 \\ 0.1 & 0.8 & 0.1 \\ 0.5 & 0.1 & 0.4 \end{array} \right).$

For example the 0.8 in row 2, column 2 shows that there is a 0.8 chance of starting at home (state 2) and ending at home in one hour. Then, we can use matrix multiplication to calculate the probability of where we'd be after two hours (note we're using the same arrow notation as we did above):

$M^2 = \left( \begin{array}{ccc} p(m_{1\rightarrow 1}) & p(m_{1\rightarrow 2}) & p(m_{1\rightarrow 3}) \\ p(m_{2\rightarrow 1}) & p(m_{2\rightarrow 2}) & p(m_{2\rightarrow 3}) \\ p(m_{3\rightarrow 1}) & p(m_{3\rightarrow 2}) & p(m_{3\rightarrow 3}) \end{array} \right) = \left( \begin{array}{ccc} 0.52 & 0.17 & 0.31 \\ 0.19 & 0.66 & 0.15 \\ 0.51 & 0.17 & 0.32 \end{array} \right).$

This shows that after two hours there is (for example) a 0.19 chance that someone who started at home (state 2) is now found at the beach (state 1).

After 24 hours we have the following probability matrix:

$M^{24} = \left( \begin{array}{ccc} p(m_{1\rightarrow 1}) & p(m_{1\rightarrow 2}) & p(m_{1\rightarrow 3}) \\ p(m_{2\rightarrow 1}) & p(m_{2\rightarrow 2}) & p(m_{2\rightarrow 3}) \\ p(m_{3\rightarrow 1}) & p(m_{3\rightarrow 2}) & p(m_{3\rightarrow 3}) \end{array} \right) = \left( \begin{array}{ccc} 0.407 & 0.333 & 0.260 \\ 0.407 & 0.333 & 0.260 \\ 0.407 & 0.333 & 0.260 \end{array} \right).$

So we notice the same situation as last time – as the number of hours increase it gets less important where we started from. We can see that, to three significant figures, it doesn't now matter where we started – the probability after 24 hours of being found on the beach is 0.407, the probability of being found at home is 0.333 and the probability of being found diving is 0.260.

Hopefully this is a quick example to demonstrate the power of Markov chains in working with probabilities. There is a lot more to explore!

About the article

Andrew Chambers has an MSc in mathematics and is a teacher at the British International School Phuket, Thailand. He has written news and features articles for the Guardian, Observer and Bangkok Post, and was previously shortlisted for the Guardian's International Development Journalist of the Year Awards. Combining his love of both writing and mathematics, his website ibmathsresources.com contains hundreds of ideas for mathematical investigations (and some code breaking challenges) for gifted and talented students.

This article first appeared on ibmathsresources.com.

Comments

Markov chains

A lovely elegant exposition. Thank you!

Markov Chains

Nice demonstration, easily understood!