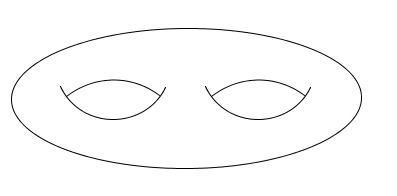
Making a double torus from an octagon
In our example the reflected copies of the original triangle form an octagon:
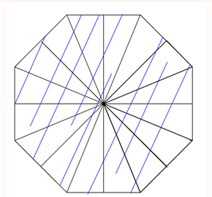
The reflection process tells us that opposite sides of this octagon need to be glued together (you can check this out for yourself). To see that this gives us a torus with two holes, first imagine that the octagon comes from a square that has had its corners cut off:
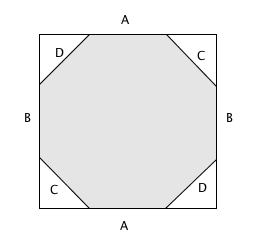
We have labelled the sides of the octagon that need to be glued together by the same letters. We first start by gluing the A and the B sides. If we glue the corresponding opposite sides of the square the octagon sits in, we get an ordinary torus. Since the octagon comes from cutting off the corners of the square, the shape we get when gluing the opposite A and B sides of the octagon is a torus with a rhombus shaped gap in it, with the gap corresponding to the cut-off corners:
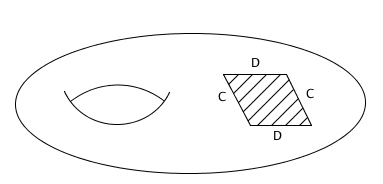
Now we glue the two D sides of the rhombus shaped hole. This creates two new gaps, whose boundaries correspond to the C sides:
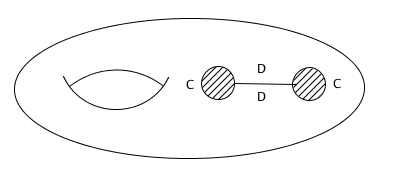
Gluing those two boundaries together bends the torus around and connects it up to form a torus with two holes: a double torus!