
Maths in a minute: Equal temperatures
At every given point in time there are two points on the equator of the Earth that have the same temperature.
How do we know this? Well, here's a proof. Let's look at the equatorial plane which slices through the Earth at the equator. The equator is a circle which lies in that plane, and we can choose a coordinate system on the plane so that the point $(0,0)$ lies at the centre of the equator. For each point $x$ on the equatorial circle there is a point $-x$ which lies diametrically opposite $x$.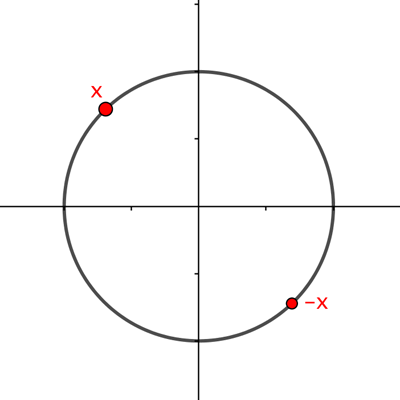
Points x and -x.
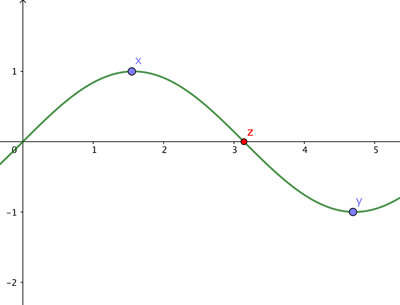
Illustration of the intermediate value theorem. If t(x)>0 and t(y)0 and t is continuous, then there is a point z between x and y such that t(z)=0.
The result actually holds for any circle on the Earth, not just the equator. In fact, the result is the one-dimensional case of the Borsuk-Ulam theorem, which says that for any continuous function $t$ from the circle to the real numbers there is a point $x$ such that $t(x)=t(-x).$
The more general version of the Borsuk-Ulam theorem says that for any continuous function $t$ from the $n$-sphere to the set of $n$-tuples of real numbers there is a point $x$ such that $t(x)=t(-x)$.
Comments
Simon
I'm sure I am missing something, but for this continuous function there is 'a' maximum value and 'a' minimum value, (1st moment =o) this is only at a single (x) value?
Christopher
The theorem states that there are two points on the equator with the same temperature. It does NOT state that for any given temperature found on the equator there is another at that same temperature.
Ken Williams
Hi there, this is a great article, but I wanted to point out that the first sentence:
At every given point in time there are two points on the equator of the Earth that have the same temperature.
is probably not what you intended, since it's much more trivially true and not very impressive. I'm assuming you meant to write something like this:
At every given point in time there are two DIAMETRICALLY OPPOSED points on the equator of the Earth that have the same temperature.