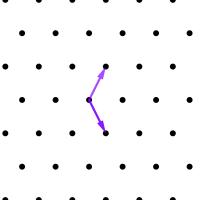
Maths in a minute: Lattices
A lattice is essentially a regular grid of points generated by arrows.
Imagine a dot in the plane. Draw two arrows starting at that dot, which aren't parallel to each other. Now also draw the same two arrows, but facing in exactly the opposite direction from the first two. Draw a new dot at the tip of your four arrows.
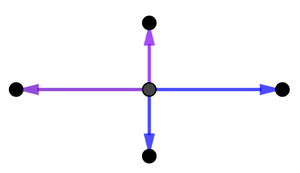
Now draw the same four arrows for each of your new points. This gives you another generation of points at the tips of the new arrows.
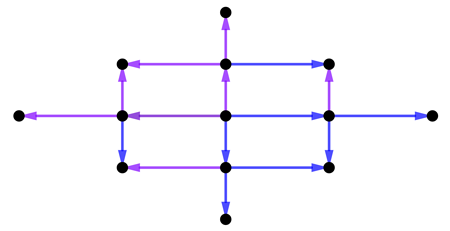
Now do the same for all the new points, drawing four arrows each for the new generation of points. If you keep going like this, you eventually fill the whole plane with a grid, called a lattice. The pair of arrows which generated this lattice is called the basis of the lattice.
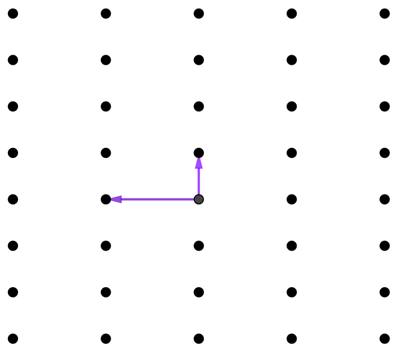
Mathematically, the arrows are called vectors. Every point in the lattice comes from an integer combination of the two basis vectors. For example, in the image below, the point P is given by v+w because you get to it by following one copy of v and then one copy of w, where v and w are the two basis vectors. The point Q is given by -v+2w because you get to it by following one copy of v but in the opposite direction (hence the minus) and then two copies of w.
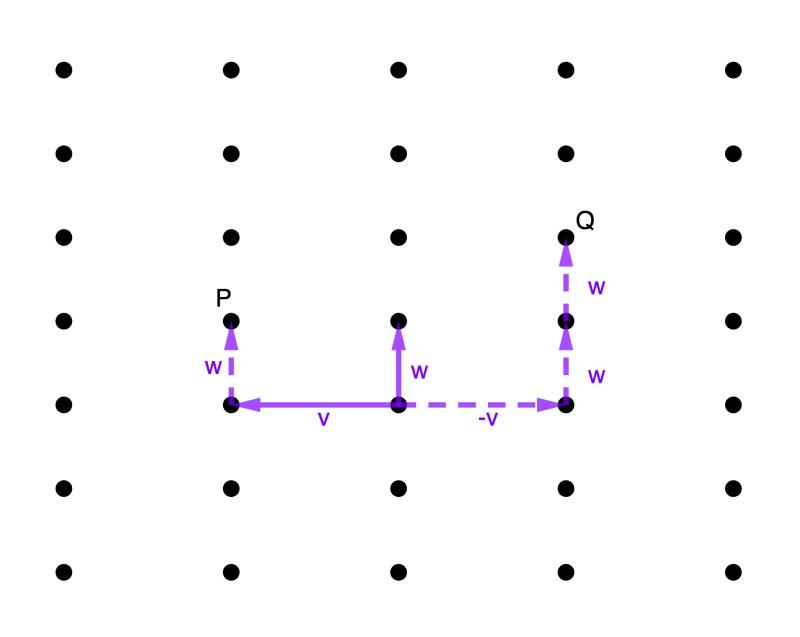
In our example, the lattice points define rectangles. That's because there's a right angle between the two basis vectors. But this doesn't have to be the case. Here is an example of a lattice that isn't:
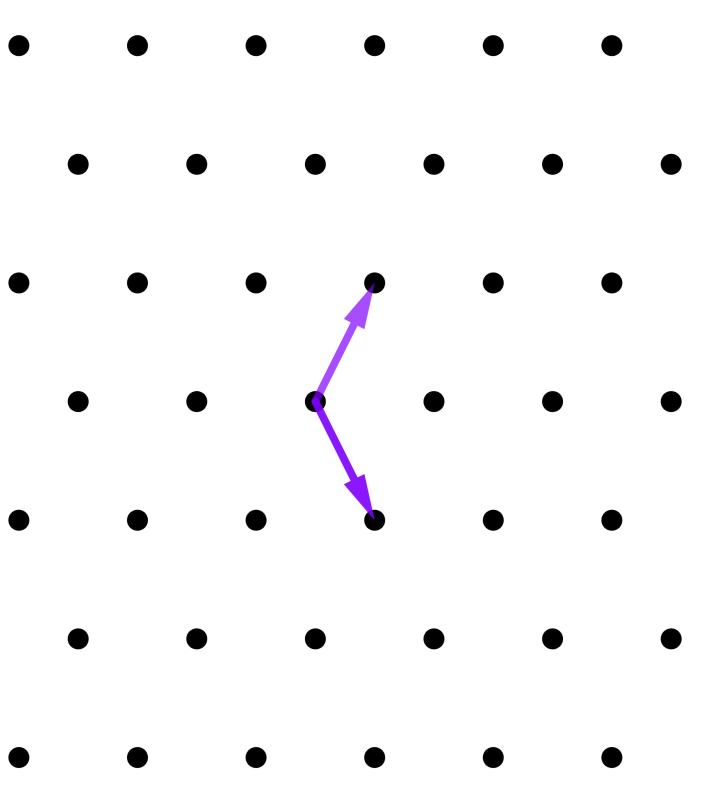
(Technically, a lattice comes from integer combinations of vectors that together form a basis of the underlying vector space, see more here.)
Finally, note that the same lattice can have different bases. In the example below, two different pairs of arrows give you the same lattice.
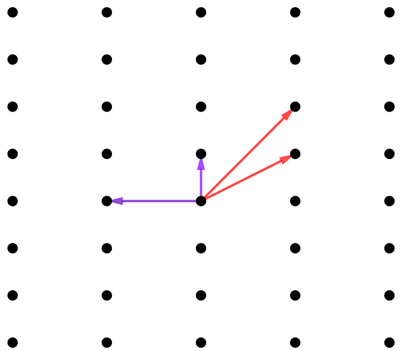
Then any point in your lattice can be generated by both basis pairs. In the example we saw above, you can get to the point P below by following one of the purple basis vectors by the other. But you can also get to the point P by starting with two copies of one of the red basis vectors, followed by three opposite copies of the other red basis vector.

You can also play the game of producing a lattice using vectors in three-dimensional space. And since mathematicians have a way of thinking about the 4th, 5th, 6th, or any higher dimension, they can define lattices and their bases in any dimension.
The basis reduction problem
There are many interesting problems to do with lattices. Here's one: given a lattice (in any dimension), can you find a basis whose vectors are as short as possible (see here for the precise meaning of this) and as close as possible to orthogonal to each other (that is, have right angles between the pairs of vectors)? (The purple basis in the image above is an example of this "good" or reduced basis for this example lattice.)
When we're looking at a lattice in a plane, as in our example, there's an efficient algorithm to solve this lattice reduction problem. But that's not the case when you look at higher-dimensional lattices. Such hard problems in high-dimensional lattices are the key to lattice-based cryptography,thought to be the best cryptography technique for keeping information safe in the advent of quantum computing.
You can find out more about lattice-based cryptography here and more details about research into lattices here.
This introduction is drawn from the article László Lovász: Working mathematical miracles about the work of László Lovász, the winner of the 2021 Abel Prize.
This article was produced as part of our collaborations with the Isaac Newton Institute for Mathematical Sciences (INI) and the Newton Gateway to Mathematics.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. The Newton Gateway is the impact initiative of the INI, which engages with users of mathematics. You can find all the content from the collaboration here.
