
Lattice-based cryptography
Today we all rely on cryptography to keep important information safe, such as protecting our credit card details every time we shop online. Current cryptography techniques are currently secure, even against attacks using the fastest computers. But when large-scale quantum computers become available these systems will become vulnerable. (You can read more about why in this article.)
The best candidate for post-quantum cryptography – that is cryptography techniques that will be secure even in the face of attacks by quantum computers – is lattice based cryptography.
Public-key cryptography, such as RSA and elliptic curve cryptography, rely on having a mathematical problem that is easy to calculate in one direction but hard to solve in the other. The mathematical problem operates like a metaphorical padlock that is shared publicly. Everyone has a personal padlock they open and publicly share with anyone who wants to send them a message. Then you can securely send someone a message by putting it in a metaphorical box and snapping shut the recipient's personal padlock. Only the recipient can unlock the padlock with their own private key.
For RSA the mathematical problem is factoring large numbers. While it is easy to multiply to numbers together, it is very hard to find the prime factors (numbers only divisible by 1 and themselves) of very large numbers. These prime factors provide the key to unlock the metaphysical padlock in RSA. (You can read more about RSA cryptography here.)
For post-quantum cryptography we need a mathematical problem that even a quantum computer cannot solve (to the best of our knowledge). The top current candidate is based on the mathematics of lattices.
You can think of a two-dimensional lattice as a grid of dots on an infinitely large page. Such a lattice is generated by a pair of vectors (you can think of these arrows drawn on the page) that are called a basis for the lattice. So any point in the lattice can be described by adding together copies of the basis vectors (ie, by laying copies of the basis vectors nose to tail – you can see examples of this in the picture below). (You can read an easy introduction to lattices here.)
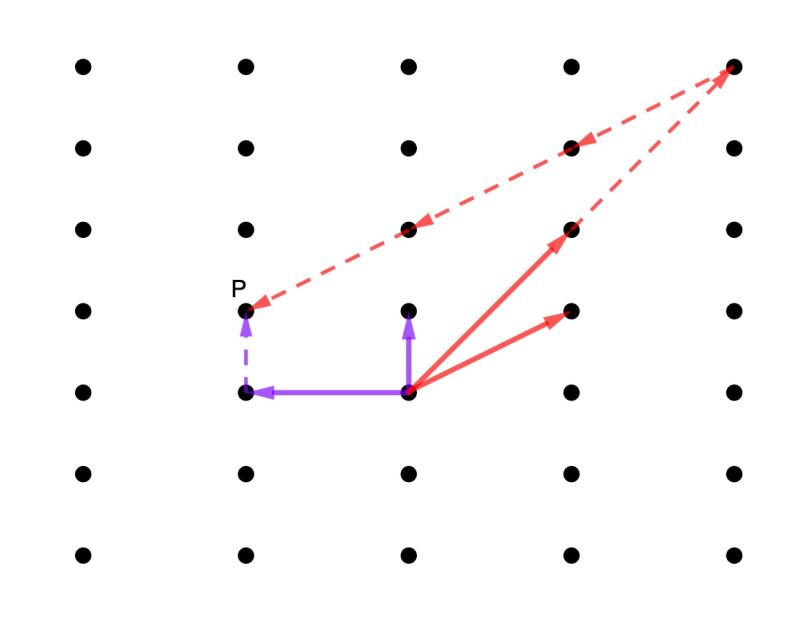
You can have more than one basis for a lattice – see the example in the image above – but not all bases are equally good. Certain bases are thought of as "good", and are called reduced bases. (In our example above the pair of purple basis vectors is the reduced basis, as opposed to the red pair of basis vectors.) Using the reduced basis to describe points in your lattice makes solving questions about your lattice much easier than if you were using a "bad" basis.
Finding a needle in a haystack
We heard about lattice-based cryptography from Zygmunt Lozinski, from IBM Research, in his talk at an event organised by the Newton Gateway to Mathematics, held as part of a longer research programme at the Isaac Newton Institute for Mathematical Sciences in Cambridge.
Lozinski gave an example of a lattice problem that can be used in lattice-based cryptography. This problem is called the closest vector problem: if you have a point Q that is not directly on your lattice, what point on your lattice is closest to the point Q? It's easy to see the closest point on the lattice in our two-dimensional example. But the lattices used in lattice-based cryptography have hundreds or thousands of dimensions. Lozinski described finding the closest point in such high-dimensional lattices as like "finding a needle in a haystack."
This challenge can be used in cryptography as follows. Suppose you want to send someone a message and you can encode that message as a point in a very high-dimensional lattice. (A simplified example might be encoding the message as a combination of the basis vectors. If you want to say "hi", your message could be encoded as 8 times the first basis vector and 9 times the second basis vector – to represent the "h" and the "i" as the 8th and 9th letters in the alphabet.)
Your intended recipient has publicly shared their personal, mathematical padlock – for lattice-based cryptography the open padlock is a "bad" basis for their personal lattice. You can then encode your message in terms of this bad basis (8 times the first basis vector and 9 times the second). And to snap the padlock shut you add a small random amount to the coordinates of your encoded point, to bump it off the lattice.

Now you have a mathematical haystack – the multitude of points in the very high-dimensional lattice that are in the region of this encoded message. It is currently not feasible to find the closest point on the lattice, to solve the closest vector problem, using either a classical or a quantum computer. The only feasible way to answer it, to unlock the padlock, is if you have the reduced basis for the lattice. (As we mentioned above, having the reduced basis makes answering lattice problems much easier.) The reduced basis acts as the private key of the mathematical padlock.
You can read a more detailed explanation of how this lattice problem can be used for cryptography in this great Medium article by Nicklas Körtge. And you can read more about the post-quantum cryptography in our article.
About this article
This article is part of our coverage of Quantum Computing: Applications and Challenges, an event organised by the Newton Gateway to Mathematics as part of the Quantum information, quantum groups and operator algebras programme at the Isaac Newton Institute for Mathematical Sciences in Cambridge.
Zygmunt Lozinski is a Senior Technical Staff Member in IBM Research, where he is responsible for making the world’s networks quantum-safe. He was one of the speakers at the event.
Rachel Thomas is Editor of Plus
This article was produced as part of our collaborations with the Isaac Newton Institute for Mathematical Sciences (INI) and the Newton Gateway to Mathematics.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. The Newton Gateway is the impact initiative of the INI, which engages with users of mathematics. You can find all the content from the collaboration here.
