New understanding of a neglected disease

"I believed mathematics would be a catalyst to solving problems," says Fatumah Atuhaire. Her second Masters degree, in mathematical ecology at the African Institute of Mathematical Sciences (AIMS), South Africa, had already opened her eyes to the power of maths to solve problems in the home countries of her and her colleagues at AIMS. "I believed a PhD would open my mind to new horizons, not only in research... but in how things are done in places beyond Africa. To translate that knowledge and bring that skill set back home."

Fatumah Atuhaire after her PhD viva, with Christine Currie and Rebecca Hoyle

Fatumah Atuhaire (centre) after her PhD viva, with Christine Currie and Rebecca Hoyle (Image - Fatumah Atuhaire)

Atuhaire has just finished that PhD, working at the University of Southampton with Rebecca Hoyle and Christine Curry, and with Rachel Simmonds from the University of Surrey. Her work used the power of mathematics to help understand a neglected tropical skin disease, Buruli ulcer (BU), that occurs primarily in sub-Saharan Africa and Australia. The highest number of cases occur in children under the age of 15 living in rural tropical environments.

But despite being recorded since the 1890s very little is known about this disease, says Atuhaire. "The physiological processes that lead to the observed features in BU are still unclear." We do know that it is caused by bacteria infecting the skin and releasing a toxin that causes the skin cells to die, forming ulcers. But we still don't know how this infection happens, and there is currently no way to prevent the disease.

"When someone has contracted BU it takes a long period to get healed," says Atuhaire. Because the infection is painless people go to hospital late in the course of the infection. "Late diagnosis leads to a delay in seeking treatment. [Patients] spend a lot of time in hospital and the cost of surgical treatment is high."

Modelling how cells die

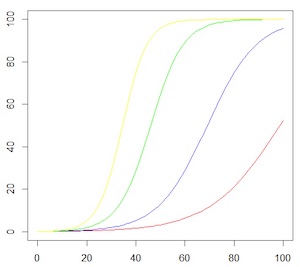
Different examples of the S-shaped curves of logistic growth

Different examples of logistic growth – initially the bacterial cells grow exponentially, but eventually plateaus out. (Image from How maths can help you get ahead of the S-curve)

Atuhaire wanted to use mathematics to describe how the bacteria that cause BU, Mycobacterium ulcerans, and the toxin this bacteria creates, spread in the skin. The number of bacterial cells in the skin will initially grow exponentially, but this growth can't carry on forever and eventually plateaus out - a process captured by Atuhaire using something called a logistic growth model. She then used a diffusion equation to model the movement in the skin of the bacteria and the toxins they produce.

Next to describe was how the infection causes skin cells to die. The toxin can kill the skin cells directly, and the toxin can also disrupt the internal structure of cells so they die indirectly from lack of oxygen. There are different types of skin cells, so to simplify the model Atuhaire classified them to either be endothelial cells (which regulate blood clotting) or stromal cells. Both types of cells are highly sensitive to the toxin.

In the case of the toxin directly causing each type of skin cell to die, if the local concentration of the toxin ( $m$ ) exceeds some threshold for those cells ( $m>c_ e$ for the endothelial cells and $m>c_ s$ for the stromal cells), then the death rate of each type of skin cells is directly proportional to the density of those cells. So there is an equation for this direct action of the toxin on each of the types of skin cells, with $i=e$ for endothelial cells or $i=s$ for the stromal cells:

$\frac{\partial n_ i}{\partial t} = -d_ i n_ i H(m-c_ i)$

The left-hand side of this equation denotes the death rate, the rate of change over time of the cell density $n_ i$ . There is a minus sign in the right hand side of the equation as the cells are dying, and this death rate is equal to some constant $d_ i$ times the cell density, $n_ i$ . The $H$ on the right-hand side is the Heaviside function, which acts a mathematical switch, turning the cell death on once the concentration of the toxin exceeds the relevant threshold.

The equation describing the indirect action of the toxin on each type of skin cell looks very similar, but this time the mathematical switch is only flipped if the concentration of the toxin exceeds the threshold of the endothelial cells (as they are the cells supporting blood flow):

$\frac{\partial n_ i}{\partial t} = -d_ k n_ i H(m-c_ e)$

where $d_ k$ is the death rate for cells due to lack of oxygen.

The power of maths

"We developed a mathematical model that describes the dynamics of the growth and diffusion of the toxin, and the decrease in the cell densities," says Atuhaire. Once enough work had been done on the model, establishing boundary and initial conditions, and using available data to estimate the parameters involved (such as the direct death rates $d_ e$ and $d_ s$ , the indirect death rate $d_ k$ , and the thresholds for the Heaviside functions), Atuhaire and her colleagues could use a computer to run the model, solving the equations numerically.

One key contribution of Atuhaire's work was that her model could separately explore the toxin's direct and indirect mechanisms of killing skin cells, as well as bringing both these mechanisms together. "The model provides more understanding of how lesions form," says Atuhaire. "You can switch the two mechanisms on and off – something that may not be possible to do experimentally." And her results echo the observed role of the toxin in the progression of BU. In particular, she could predict that the first drop in the density of skin cells occurs 12 days after infection, signifying the death of these cells when both mechanisms were switched on and the concentration of the toxin has reached the threshold.

Atuhaire was also able to use the model to predict how quickly the wounds would grow, which could lead to strategies for improving treatment. Particularly with surgical treatment in the later stages of the disease: "knowing how far the tissue has degraded is influential in treatment decisions."

A world map showing the numbers of cases of Burulia ulcer reported in 2022. The highest number of cases occur in sub-Saharan Africa and in Australia, with little or no cases reported elsewhere.

Number of cases of Buruli ulcer reported in 2022 (Image WHO – CC BY-NC-SA 3.0 IGO)

Another impact of Atuhaire's work also comes from one of the challenges she faced in her PhD. So much is still unknown about the disease and there is still a lack of enough literature and data to use in estimating the parameters used in the model. "Unavailability of experimental data posed challenges for model verification, a common problem for these diseases," says Atuhaire. "We can use this model to suggest the type of data that should be collected as research of BU evolves."

Black heroes of mathematics

Atuhaire was speaking at the fourth annual Black Heroes of Mathematics conference: "a showcase of inspirational role models in the black community and their contribution to maths and education," said one of the organisers, Nira Chamberlain. One of the highlights of the conference is the range of speakers it brings together, from practising mathematicians to teachers and educational researchers. Mathematics researchers and mathematics educators don't always get a chance to hear from different areas within their own fields, let alone hear each such a wide range of research from each other's fields.

We found perspectives from the experts in maths education particularly enlightening. Nicole Joseph, Peabody College, studies the experience of black girls in maths education in the US. Joseph explained how racialised and gendered stereotypes get in the way of black girls' path to becoming strong mathematicians. The way we expect students to behave is alienating for many young people, Joseph says, and particularly for black girls, who reported being told not to joke and that they were too loud and talkative. Social interaction and humour is such a valuable and treasured part of being a working mathematician – why are we trying to eradicate that in the classroom?

Joseph believes the key to succeeding in maths is to be able to develop a mathematical identity – a person must be able to have an inherent sense that they are a mathematician. But existing methods used in research to assess this sense of mathematical identity did not account for the intersections of race and gender. Joseph has developed a new measure that broadens these existing methods by also considering the assets and the barriers that this intersectionality can bring.

"Maths is such a power," says Joseph. "Being literate in maths is super important. We live in a technological world and if you don't understand these things you'll get left behind." The research and the researchers highlighted by this conference give us all insight into how we can support future black heroes of mathematics and the important work they will do.

About this article

This article is based on talks given by Fatumah Atuhaire, University of Southampton, and Nicole Joseph, Peabody Colleage, Vanderbilt University, at the Black Heroes of Mathematics (BHoM) conference in October 2023.

BHoM is held each year by The African Institute for Mathematical Sciences (AIMS), British Society for the History of Mathematics (BSHM), ICTP-East African Institute for Fundamental Research (ICTP-EAIFR), Institute of Mathematics and its Applications (IMA), International Centre for Mathematical Sciences (ICMS), Isaac Newton Institute (INI), London Mathematical Society (LMS) and Mathematical Association (MA).

Rachel Thomas is Editor of Plus.

This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.

The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.