Go back to the first page of this article.

When the answers to complicated calculations show up simple patterns, then that's an indication that you might be looking at things in the wrong way. Shifts of view point can be eye opening. When I describe a table full of billiard balls to you, the initial instinct is to tell you their locations. But if they are moving, especially if they are moving very fast, it might be better to tell you their momentum (their velocity times their mass). Describing the balls in momentum space might reveal patterns, such as all balls are moving in parallel, that a visual snapshot of the table would conceal.

Momentum space is often used in quantum field theory, the framework that underlies the standard model of particle physics, which describes all the fundamental forces except for gravity. Gravity is dealt with by Einstein's theory of relativity, which takes ordinary space and time, combined into spacetime, as the stage on which physics unfolds. The greatest problem of modern physics is that quantum field theory and relativity don't get along. Any naive attempt to combine the two leads to non-sensical maths and deep paradoxes. So in the 1960s Roger Penrose developed a mathematical structure called twistor space which carries echoes of both momentum space and Einstein's spacetime. This, he believed, was more fundamental and might provide the backdrop against which relativity and quantum field theory might be married up.

Twist it!

Twistor space never quite caught on, but in 2004 Edward Witten, a towering figure in theoretical physics, decided to see what would happen if you translated MHV amplitudes into this exotic construct. His effort was rewarded: the gluons involved in the interaction were represented in twistor space by points arranged neatly along a straight line. Suddenly the simplicity of the MHV amplitude was explained: it's simple because it corresponds to a particularly simple configuration of gluons, which only shows up in twistor space.

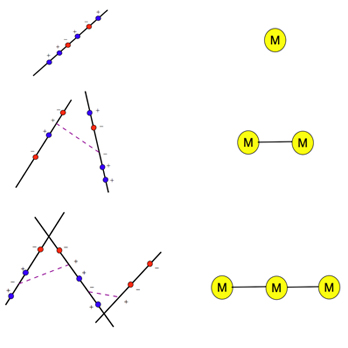
Figure 3: The MHV amplitude corresponds to a straight line in twistor space (top left). The next-to, next-to-next-to, etc, MHV amplitudes correspond to collections of lines.

Witten also considered progressively more complicated amplitudes, called next-to-MHV, next-to-next-to-MHV, and so on. These didn't normally reveal any particularly nice structure, but surprisingly, when translated into twistor space, they corresponded to collections of intersecting lines (see figure 3). "There was a matching of the two sides, and this immediately fascinated many people," says Travaglini.

This gave Witten, and his colleagues Freddy Cachazo and Peter Svrcek, an idea: perhaps all gluon amplitudes could be calculated using MHV amplitudes as basic ingredients. "We can symbolise this by a blob and call it MHV," explains Brandhuber. "Then, for these next complicated amplitudes, you just have to combine two such MHV Amplitudes, very much like what you do with the usual Feynman diagrams." (See figure 3.) The result was an extremely efficient way of calculating even more complicated, non-MHV amplitudes. And since each MHV amplitudes already involves any number of particles, one simple MHV blob holds inside itself a large number of Feynman diagrams.

This was neat, but it was only a beginning. Witten and his colleagues had only computed tree-level amplitudes with their diagrams; the dreaded loops were still missing. Secondly, they were working within an idealised model of the world. The fact that this model wasn't realistic didn't matter if you were considering loop-less diagrams, but once loops came in, it would. At a conference in Paris in June 2004 Witten threw down his challenge: Learn to calculate loops!

The return of the S-matrix

Brandhuber, Spence and Travaglini had already started to work on this problem and were close to finding the right answer for the loops. Other colleagues, however, were discouraged, since Witten himself was sceptical that it could be done. "Many people listened very much to Witten, so they didn't even try; others tried and made mistakes," says Brandhuber. "Witten very much polarises the field. That can distract people in the wrong direction." But Brandhuber, Spence and Travaglini were strangers to the area. "We knew almost nothing about the field; just enough to penetrate but not to have too much background information to distract us. If you want some fresh ideas, you had better enter a new field. If you paddle around in the pool too much, you are too influenced by knowledge that is already around, you don't think outside the box."

So the three decided to give it a go anyway. They started with one-loop MHV amplitudes that had already been calculated and, using inspiration from twistor space, figured out how one-loop diagrams should work. Backing them up with maths was a challenge, but help came from an unexpected direction. During the 1960s physicists had very nearly given up on quantum field theory: it had done well in describing the force of electromagnetism and its twin sibling, the weak nuclear force. But the next force on the list, the strong nuclear force, just wouldn't yield. People became worried they might be barking up the wrong tree. Some decided to throw out quantum field theory altogether and instead try and calculate scattering amplitudes based on a different set of assumptions. Eventually quantum field theory leaped ahead again, and the alternative approach, called S-matrix theory, fell by the way side.

"[When we started working on MHV diagrams] we were at a conference in Swansea in March 2004, celebrating the birthday of one of the fathers of the S-matrix theory, the late David Olive." recalls Travaglini. "There were older people talking about [S-matrices], and we suddenly started making connections between this older approach and all the new pictures that we were drawing. [We realised] that we should be getting precisely what these people from the 1960s were discussing."

"We were lucky that this old book was lying around," says Brandhuber. "It was completely dusty. It was from 1967, one year before I was born. We thought, 'this might be interesting.'" And they were right: the mathematics of S-matrices was exactly what they needed. Their diagrams gave the correct results for the known one-loop MHV amplitudes. And they work for more general, non-MHV amplitudes too, giving results that were previously unknown. One of their one-loop MHV diagrams corresponds to a huge number of Feynman diagrams — for example, a process with 7 gluons at one loop would correspond to one MHV diagram and 227,585 Feynman diagrams!

Since the initial success others have gone on to perfect the methods. "Many other developments came in," says Brandhuber. "They were even more efficient, so we didn't try any harder to push this. If you find something else even faster, that is fine. We are not totally sure if [our method] works for higher loops, but at the practical level, that is not too important. What is needed for the LHC are one-loop calculations."

But MHV diagrams are not just glorified calculators. The results have revealed hidden structures within scattering amplitudes; structures you simply wouldn't see even if you looked at gazillions of Feynman diagrams. The link to twistor space suggests that space and time as we know it may not be as fundamental as we think. Some people have taken these ideas further and constructed theories for particle physics that no longer rely on the basic tenets of quantum field theory (see for example this article). The hope is that such reformulations may one day help us to achieve the holy grail of modern physics, to unify quantum theory and relativity. As it stands these new theories are hypothetical and it will take a long while until we find out if they are correct. What seems certain, and the physics of the last 120 years or so has proved it again and again, is that reality is far stranger than our experience suggests.

About this article

This article is part of the Researching the unknown project, a collaboration with researchers from Queen Mary, University of London, bringing you the latest research on the forefront of physics. Click here to read more articles from the project.

Marianne Freiberger, Editor of Plus, interviewed Andreas Brandhuber and Gabriele Travaglini in London in November 2013.

Andreas Brandhuber.

Gabriele Travaglini.