Plus Magazine
Independence Day: solution
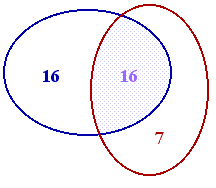
Let's suppose the two examiners found A and B errors respectively and that they found C of them in common. Now assume that A has a probability a of detecting a mistake, while B has a probability b of detecting a mistake. If the total number of typographical errors in the thesis was T, then A=aT and B=bT.
But if the two examiners are proof-reading independently then we know that C=abT. So AB=abT2=CT and so the total number of mistakes is AB/C, irrespective of the values of a and b.
Since the total number of mistakes that the examiners found (noting that we musn't double count the C mistakes that they both found) was A+B-C, this means that the total number that they didn't spot is just T-(A+B-C) and this is (A-C)(B-C)/C. In words, it's the product of the number that each found that the other didn't divided by the number they both found.
This makes good sense. If both found lots of errors but none in common then they are not very good proof-readers and there are likely to be many more that neither of them found.
In my example A=32, B=23, C=16 and so the number of unfound errors is expected to be (16x7)/16=7.
Back to Outer space: Independence Day