Puzzle page

Issue 39
Submitted by plusadmin on June 1, 2006
in
June 2006

A proof with a hole: $\pi $ equals 2

Forget all that business about $\pi $ being an irrational number with infinitely many decimal places: I can prove conclusively that $\pi $ is equal to 2.

First of all, let's recall that $\pi $ is defined to be the ratio between the circumference and the diameter of a circle, which is the same regardless of the size of the circle. So, using the notation of the diagram below, we have $\pi $ = c/d.

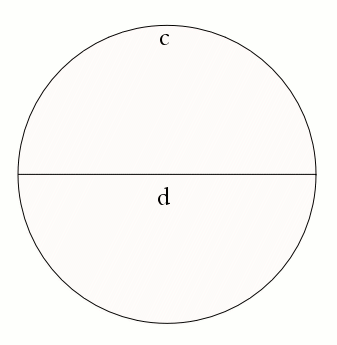
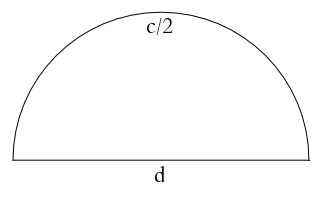
Now let's start with a circle of circumference 2, and only consider one half of it, as shown in the figure. Since it's exactly one half of the circle, the length of this semi-circle is 1. Now let's divide in half the diameter d of the circle, and draw a new, smaller semi-circle on each of the two halves. Since the ratio between diameter and circumference is the same for any circle, you can work out that the two smaller semi-circles — which are built on half the diameter of the larger one — have circumference half that of the larger one. In other words, the length of each of the two smaller semi-circles is 1/2.

Now continue in the same manner: divide the original diameter d into 4 equal pieces and draw on each of them a semi-circle of length 1/4; then divide it into 8 equal pieces and draw on each of them a semi-circle of length 1/8, etc, etc. After n steps you have 2n semi-circles, each of length 1/2n.

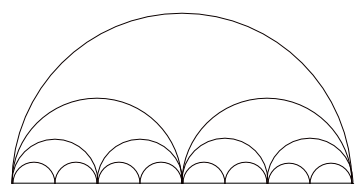
Obviously, the semi-circles get smaller and smaller at each stage, and after a great number of steps, your string of semi-circles will hardly be distinguishable from the straight line which forms the diameter of the largest circle. The string of semi-circles approximates the diameter d, and the approximation gets better and better the more steps you take. This means that the lengths of the semi-circles all added up approximate d. In fact, d is the limit of this sum as the number of steps n tends to infinity:

d = limn→∞ 2n×1/2n = 1.
We know that the circumference c of the large circle is 2, so $\pi $ = c/d = 2/1 = 2, which proves my claim. Or have I made a mistake?

If you are stumped by last issue's puzzle, here is the solution.

For some challenging mathematical puzzles, see the NRICH puzzles from this month or last month.

Solution link: 
A proof with a hole solution