A proof with a hole: $\pi$ equals 2

Forget all that business about $\pi$ being an irrational number with infinitely many decimal places: I can prove conclusively that $\pi$ is equal to 2.

First of all, let's recall that $\pi$ is defined to be the ratio between the circumference and the diameter of a circle, which is the same regardless of the size of the circle. So, using the notation of the diagram below, we have $\pi$ = c/d.

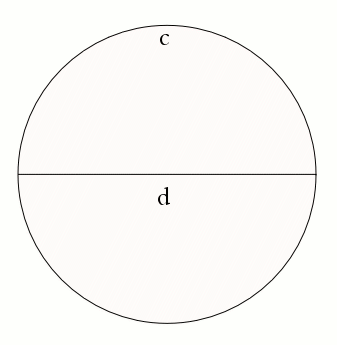
Now let's start with a circle of circumference 2, and only consider one half of it, as shown in the figure. Since it's exactly one half of the circle, the length of this semi-circle is 1. Now let's divide in half the diameter d of the circle, and draw a new, smaller semi-circle on each of the two halves. Since the ratio between diameter and circumference is the same for any circle, you can work out that the two smaller semi-circles — which are built on half the diameter of the larger one — have circumference half that of the larger one. In other words, the length of each of the two smaller semi-circles is 1/2.

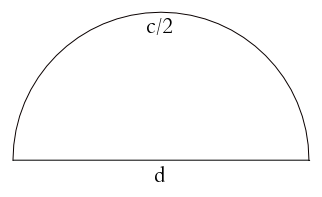
Now continue in the same manner: divide the original diameter d into 4 equal pieces and draw on each of them a semi-circle of length 1/4; then divide it into 8 equal pieces and draw on each of them a semi-circle of length 1/8, etc, etc. After n steps you have 2ⁿ semi-circles, each of length 1/2ⁿ.

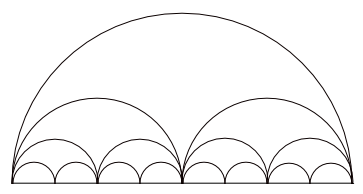
Obviously, the semi-circles get smaller and smaller at each stage, and after a great number of steps, your string of semi-circles will hardly be distinguishable from the straight line which forms the diameter of the largest circle. The string of semi-circles approximates the diameter d, and the approximation gets better and better the more steps you take. This means that the lengths of the semi-circles all added up approximate d. In fact, d is the limit of this sum as the number of steps n tends to infinity:

d = lim_n→∞ 2ⁿ×1/2ⁿ = 1. We know that the circumference c of the large circle is 2, so $\pi$ = c/d = 2/1 = 2, which proves my claim. Or have I made a mistake?

The solution

What's wrong here? Well, it is definitely true that after n steps there will be 2ⁿ semi-circles, each of length 1/2ⁿ. It is also true that the diameter of the largest circle is in some sense a limit of the strings of semi-circles: by making n large enough, you can ensure that the nth string of semi-circles squeezes as closely to the diameter d as you like.

The mistake lies in the next step: the assumption that the lengths of the strings of semi-circles tend to the length of the diameter. This is false! What happens in fact is that while at each stage we replace the semi-circles involved by smaller ones, these also become more numerous, so that the replacement makes no difference at all to the overall length. Every string of semi-circles has length 1, since

2ⁿ×1/2ⁿ = 1,

for any n. We've simply replaced a number of big wriggles by a greater number of smaller wriggles without changing the length.

The lesson is, when it comes to things like length, don't be fooled by appearance. A curve may look like a straight line, but it may be so wriggly at a small scale that in fact it's a lot longer than the line. Even worse, a set may look like a decent curve that should have finite length, but may in fact be infinitely long. And what exactly do we mean by "length" anyway? For an example of a curve with infinite length, check out the Koch curve in Plus article Jackon's fractals. And to learn about notions of length read Plus article Measure for measure.

---

Back to main puzzle page