
Wavelets catch Abel Prize

Yves Meyer. Photo: B. Eymann/Académie des Sciences.
This year's Abel Prize has been awarded to Yves Meyer for the development of an incredibly powerful mathematical tool: wavelet theory. The theory enables you to break all sorts of different types of information into simpler components which are easier to analyse, process and store — which is why it finds applications in a huge range of areas, from medical imaging to the detection of gravitational waves.
The inspiration for Meyer's work came, not from within mathematics, but from the oil industry. In the 1980s the French engineer Jean Morlet wondered how to best use seismic data to find oil: if you send vibrations into the ground, how can you use their echo to figure out where the oil is hiding? Morlet, together with the physicist Alex Grossmann, came up with a way of analysing the signals, and also coined the term "wavelet", but the oil industry wasn't interested. Morlet's method wasn't used, but it was published in a scientific journal.

This is a sine wave. It extends indefinitely to the left and right. Since sine waves are related to cosine, this could also be seen as a representation of a cosine wave.
Meyer came across Morlet's results and spotted their potential. Mathematicians and engineers already had a powerful tool for analysing and processing certain types of information. Fourier analysis, as it's called, is best explained using sound as an example. The sound of the middle A on a tuning fork is represented by a perfect sine wave, such as the one seen on the left. Other sounds, like that of a violin playing the same note, are more complicated. However, it turns out that any periodic sound, in fact any type of periodic signal, can be decomposed into a sum of sine and cosine waves of different frequencies. This enables you to do a whole range of things. For example, it enables you to manipulate the different frequencies of a sound individually, or to "clean it up" by removing interfering noise. (You can read more about Fourier analysis on Plus.)
The function f varies in time – representing a sound wave. The Fourier transform process takes f and decomposes it into its constituent sine waves, with particular frequencies and amplitudes. The Fourier transform is represented as spikes in the frequency domain, the height of the spike showing the amplitude of the wave of that frequency.
Fourier analysis is a versatile tool. It can also be used to analyse and process images and other types of information. However, it does come with a limitation: because the basic components — the sine and cosine waves — are periodic, Fourier analysis works best for repeating signals. It's not so good on non-periodic signals, which contain blips and spikes and all sorts of other irregular features. An endlessly undulating wave is no good at localising a unique feature such as a spike. Unfortunately for Fourier analysis, most real-life phenomena, from the sound of speech to seismic data, fall in the non-periodic category.
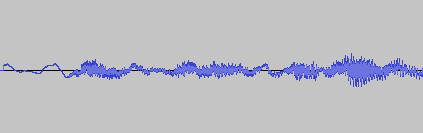
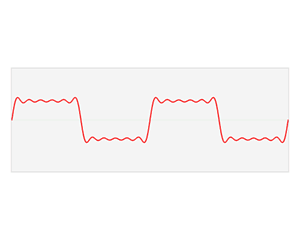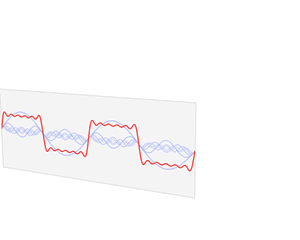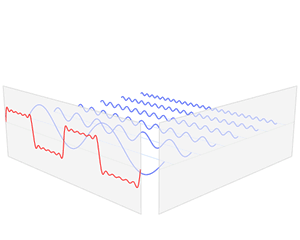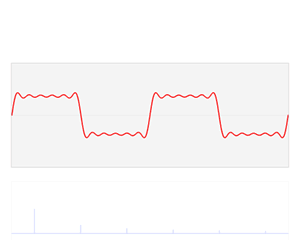
This is waveform comes from human speech. It has regularities, but it's not periodic.
This is where wavelet theory comes in. The idea is to start, not with a sine or cosine wave that's defined over all of the infinite number line, but with a piece of an oscillating function defined over just an interval. That's the mother wavelet. You can then form daughter wavelets by squashing the mother wavelet to a smaller interval (thereby increasing its frequency), expanding it over a larger interval (thereby reducing its frequency), or just shifting it along. A signal, such as the sound of human speech, is then expressed as a combination of such a system of wavelets. Such a decomposition enables you to capture repeating information in the signal, but it also allows you to zoom in on local irregularities, such as spikes, using a sequence of increasingly contracted versions of the mother wavelet.
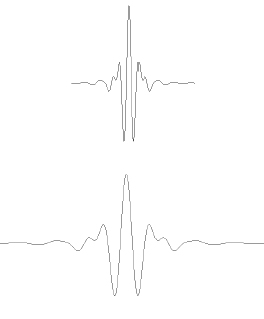
This is an example of two versions of a wavelet. A squashed version of the wavelet (above) has a higher frequency than the original version (below).
To store such a decomposition of a signal you only need the information describing the original mother wavelet, as well as the contributions of the various daughter wavelets: these are enough to put the original signal back together again. This makes wavelets a particularly useful tool for compression of information. The FBI, for example, uses wavelets to store information of fingerprints which, due to their high level of detail, would otherwise take up a huge amount of storage space.
The origins of wavelet theory go quite a long way back. The mathematician Alfréd Haar already discovered a version of a wavelet over a hundred years ago. But it was Meyer who gave the theory solid mathematical foundations. He came up with families of wavelets that exhibit the mathematical properties that are necessary for the processing and analysis of signals and developed the general mathematical framework of the theory.
Stéphane Mallat, who collaborated with Meyer on wavelet theory, calls him a "visionary" whose work doesn't belong to any one area such as pure maths, applied maths, or computer science — it can only be labelled "amazing". Apart from the prestige of the Abel Prize, awarded since 2003 to recognise "contributions of extraordinary depth and influence to the mathematical sciences", Meyer can now enjoy the 765,000 Euros that come as prize money.
Further reading
The Abel Prize website has some lovely and accessible descriptions of Meyer's work. Another good description of wavelets can be found in this article from What's happening in the mathematical sciences?