
What is the Area of a Circle?
Suppose that we are asked to find the area enclosed by a circle of given radius. A simple way to go about this is to draw such a circle on graph paper and count the number of small squares within it. Then
area contained ≈ number of small squares within circle × area of a small square.
A circle drawn on graph paper - the area inside is approximately the number of small squares times the area of each small square
If we doubled all the lengths involved then the new circle would have 4 times the area contained in the old circle
We notice that if we doubled all the lengths involved then the new circle would have twice the radius and each of the small squares would have four times the area. Thus
≈ number of small squares × area of a new small square
= number of small squares × 4 × area of a old small square
≈ 4 × area contained in old circle.
By imagining what would happen if we used finer and finer graph paper, we conclude that doubling the radius of a circle increases the area by a factor of 4.
The same argument shows that, if we multiply the the radius of a circle by $k$, its area is multiplied by $k^2$. Thus $$ \mbox{ area contained within in circle radius } r = r^2 \times \mbox{ area contained within in circle radius 1. } $$ If, following tradition, we write $$ \mbox{ area contained within in circle radius 1 }= \pi , $$ we obtain the memorable formula $$ \mbox{ area contained within in circle of radius } r = \pi r^2. $$We can now play another trick. Consider our circle of radius r as a cake and divide it into a large number of equal slices. By reassembling the slices so that their pointed ends are alternately up and down we obtain something which looks like a rectangle of height r and width half the length of the circle.

The area covered by a cake is unchanged by cutting it up and moving the pieces about.
But the area of a rectangle is
width × height
and the area of of the cake is unchanged by cutting it up and moving the pieces about. So
\begin{eqnarray*} \mbox{ half length circle }\times r & \approx & \mbox{ width of rectangle } \times \mbox{ height of rectangle } \\ & = & \mbox{ area of rectangle } \\ & \approx & \mbox{ area enclosed by circle } = \pi r^2 . \end{eqnarray*} Dividing by $r$ and multiplying by $2$, we get $$ \mbox{ length circle }\approx 2\pi r. $$ By increasing the number of slices, we can make our approximations better and better, obtaining another memorable result $$ \mbox{ length of circle with radius }r = 2\pi r. $$ The formulae we have obtained for the area enclosed and the length of a circle are very nice but we can not actually use them unless we know a good approximation to $\pi$.Approximating Pi
One approximation goes back to the ancient Greeks who looked at the length of a regular polygon inscribed in a circle of unit radius. As we increase the number of sides of the polygon the length of the polygon will get closer and closer to the length of the circle that is to $2\pi$.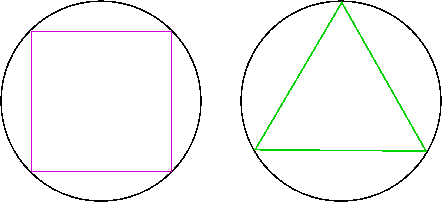
Can you compute the total length of an inscribed square? Of an inscribed equilateral triangle?

Francois Vieta
Many of the ideas in this article go back to Archimedes, but developments in mathematical notation and computation enabled the great 16th century mathematician Vieta to put them in a more accessible form. (Among other things, Vieta broke codes for the King of France. The King of Spain, who believed his codes to be unbreakable, complained to the Pope that black magic was being employed against his country.)
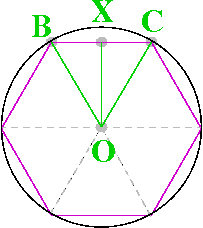
We can approximate the circle with n-sided polygon,
in this case an hexagon with n=6.
If you calculated the length of the perimeter for an inscribed square or triangle, does our general formula for an n-sided polygon agree for n = 3 and 4? If you try to use your calculator to calculate $l_5$ , $l_6$, you'll observe that the results aren't a very good approximation for $\pi$.
There are two problems with our formula for $l_n$ . The first is that we need to take $n$ large to get a good approximation to $\pi$. The second is that we cheated when we used our calculator to evaluate $\sin(180/n)$ since the calculator uses hidden mathematics substantially more complicated than occurs in our discussion.Doubling sides
How can we calculate $\sin(180/n)$? The answer is that we cannot with the tools presented here. However, if instead of trying to calculate $\sin(180/n)$ for all $n$, we concentrate on $\sin(180/4)$, $\sin(180/8)$, $\sin(180/16)$, ... (in other words we double the number of sides each time), we begin to see a way forward. Ideally, we would like to know how to calculate $\sin x/2$ from $\sin x$. We can not quite do that, but we do know the formulae (from the standard trigonometric identities)$$ \sin x = 2 \sin \frac{x}{2} \cos \frac{x}{2} $$ and $$ \cos x = \cos^2 \frac{x}{2} - \sin^2 \frac{x}{2} = 2 \cos^2 \frac{x}{2} - 1. $$ Thus $$ \cos \frac{x}{2} = \frac{1}{\sqrt{2}} \sqrt{1 + \cos x} $$ and $$ \sin \frac{x}{2} = \frac{\sin x}{2 \cos(x/2)} . $$ We can use these forumulae to find $\cos(180/2), \sin(180/2), \cos(180/4), \sin(180/4)$, ... $\cos(180/16), \sin(180/16)$. Try it out on your caculator (but don't use the trigonometric function keys) and hence find $l_{16}$ and $l_{32}$. We can make the pattern of the calculation clear by writing things algebraically. Let us take $y = 45$ and write $$ a_r = \cos (2^{-r}y), $$ and $$ s_r = l_{2^{r+2}}. $$ Then \begin{eqnarray*} s_0 & = & l_4 = 4 \sin y,\\ s_1 & = & l_8 = 8 \sin (y/2) = 4 \frac{\sin y}{\cos (y/2)} = \frac{s_0}{a_1} ,\\ s_2 & = & l_{16} = 16 \sin (y/4) = 8 \frac{\sin (y/2)}{\cos (y/4)} = \frac{s_0}{a_1 \times a_2} \end{eqnarray*} and, continuing as far as we like, we see that $$ s_n = \frac{s_0}{a_1 \times a_2 \times a_3 \times \ldots \times a_n} . $$ Thus for very large $n$ $$ \pi \approx \frac{s_0}{a_1 \times a_2 \times a_3 \times \ldots \times a_n} . $$ Since $y=45$, $s_0 = \frac{4}{\sqrt{2}}$ and $a_0 = \frac{1}{\sqrt{2}}$, and we can write $s_0=\frac{2}{a_0}$. Therefore $$ s_n = \frac{2}{a_0 \times a_1 \times a_2 \times \ldots \times a_n} . $$Vieta's formula and beyond
Although Vieta lived long before computers, this approach is admirably suited to writing a short computer program. The definitions of $a_n$ and $s_n$ lead to the rules $$ a_{n+1} = \frac{1}{\sqrt{2}} \sqrt{1 + a_n} \mbox{ and } s_{n+1} = \frac{s_n}{a_{n+1}} $$ and we can use these to easily compute successive values of $s_n$. If you have a computer or programmable calculator, see if you can compute $s_1, s_2, \ldots , s_{20}$. Nowadays we leave computation of square roots to electronic calculators, but, already in Vieta's time, there were methods for calculating square roots by hand which were little more complicated than long division. Vieta used his method to calculate $\pi$ to 10 decimal places. We have shown that $$ \frac{2}{\pi} \approx a_0 \times a_1 \times a_2 \times \ldots \times a_n , $$ and the larger $n$ is, the better the approximation. It is natural to write $$ \frac{2}{\pi} = a_0 \times a_1 \times a_2 \times \ldots \times a_n \times a_{n+1} \times a_{n+2} \times \ldots $$ where, in some sense, we multiply together an infinite number of terms. Using the rule above to write the successive values for $a_n$ (starting with $a_0=1/\sqrt{2}$), we obtain Vieta's formula: $$ \frac{2}{\pi} = \sqrt{\frac{1}{2}} \times \sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}} \times \sqrt{\frac{1}{2} + \frac{1}{2}\sqrt{\frac{1}{2} + \frac{1}{2}\sqrt{\frac{1}{2}}}} \times \ldots $$From an elementary point of view this formula is nonsense, but it is beautiful nonsense and the theory of the calculus shows that, from a more advanced standpoint, we can make complete sense of such formulae.

The Rhind Papyrus, from around 1650 BC,
is thought to contain the earliest
approximation of pi; as 3.16.
The accuracy of this approximation increases fairly steadily, as you will have seen if you used your calculator to compute the successive values of sn. Roughly speaking the number of correct decimal places after the nth step is proportional to n. Other methods were developed using calculus, but it remained true for these methods that the number of correct decimal places after the nth step was proportional to n.
In the 1970's the mathematical world was stunned by the discovery by Brent and Salamin of method which roughly doubled the number of correct decimal places at each step. To show that it works requires hard work and first year university calculus. However, the method is simple enough to be given here.
Take $A_0 = 1, B_0 = 1/\sqrt{2}$ and $S_0 = 1/2$. Let $$ A_{n+1} = \frac{A_n + B_n}{2} , B_{n+1} = \sqrt{A_n \times B_n} \mbox{ and } S_{n+1} = S_n - 2^{n+1}(A^2_{n+1} - B^2_{n+1}) $$ Then $$ P_n = \frac{2 A^2_n}{S_n} $$ is a good approximation to $\pi$. Using this algorithm, it is easy to compute the first few approximations, say P1, P2, P3 and P4, on your calculator.
Since then even faster methods have been discovered. Although $\pi$ has now been calculated to a trillion (that is to say 1,000,000,000,000) places, the hunt for better ways to do the computation will continue.
About the author

Tom Körner is a lecturer in the Department of Pure Mathematics and Mathematical Statistics at the University of Cambridge, and Director of Mathematical Studies at Trinity Hall, Cambridge. His popular mathematics book, The Pleasures of Counting, was reviewed in Issue 13 of Plus.
He works in the field of classical analysis and has a particular interest in Fourier analysis. Much of his research deals with the construction of fairly intricate counter-examples to plausible conjectures.
Comments
Anonymous
I'm a 16 years old student from Israel and really liked and enjoyed this article. In my opinion, it prooves us once more how Math is so pure and beautiful.
Anonymous
its been 10 years since you left this comment and i hope that you changed your mind about math being "pure" because this article almost gave me a stroke
Anonymous
If we are given the circumference of a circle to be 2(PI)r, then by simple calculus the area will be (PI)r^2. This comment is submitted by Peter L. Griffiths.