Sandy Black

 

At first glance, mathematics might not seem an obvious source of inspiration for a fashion designer. However Professor Sandy Black, from the London College of Fashion, explains that maths is at the very heart of the catwalk: "When somebody is designing and creating fashion to be worn on the body there's a constant movement between 2D and 3D, which is what fashion designers are doing all the time. For example pattern cutting is really quite technical and quite mathematical: it is actually a form of engineering."

Sandy is a knitwear designer, a career that has allowed her to bring together her passion for design with her love of mathematics. "I think that knitwear is a hybrid. You are making a structure from a thread, but, if you're using it for fashion clothing, you are always thinking around the body as well. And it's amazing because you can simultaneously create a fabric and shape it with knitting."

A one-dimensional thread creating a two-dimensional fabric for a three-dimensional body

"I always enjoyed maths at school, the logic, the problem solving, and the purity of it, and I liked the visual side of geometry," says Sandy. "I was particularly attracted to tiling patterns and repetition, which are an absolute necessity for textiles." And here she discovered an inspiration that crossed over from maths to art. "One of my inspirations has always been tiles and piecing things together." In future knitwear designs, Sandy would construct complex pieces from tilings, fitting separately knitted shapes together.

Art has also always been an important part of Sandy's life. "I love drawing. I didn't do fashion drawings [at school], I just used to draw from life." One of her early artworks, a design based on a contour map, was used for a school magazine cover. "I liked design drawing and I think those were signs that I was interested in design really from quite early."

Sandy was able to study both maths and art initially, but at O-level (the equivalent of GCSE) she had to make a choice as the curriculum structure did not allow her to continue to study both. "That was quite hard. I did science A-levels because at that time the prospects were felt to be very strong in the sciences. I did physics, chemistry, maths, further maths and special maths. And I did enjoy it, aesthetically right the way through to the problem solving side."

"I was getting involved in number and series and all those lovely things. I remember discovering On Growth and Form which I thought was absolutely fantastic; the correlation between mathematics and things in the natural world. Also I adored Escher, his work was really inspiring because it was an approach that nobody else had taken." So after high school Sandy moved from Leeds and Yorkshire, where she had been brought up, to study pure and applied mathematics at University College London.

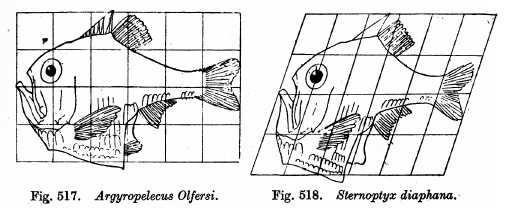
The transformation of Argyropelecus olfersi into Sternoptyx diaphana by applying a 70° shear mapping.
[From "On Growth and Form", by D'Arcy Wentworth Thompson, Cambridge University Press,
1917, 1942, 1952. Reprinted with permission.]

However Sandy was surprised to find that at university she preferred the practical over the theoretical: "I was a bit disappointed to be honest! I enjoyed the applied maths much more than the pure maths, which I didn't expect. I thought I was someone who enjoyed being in the nth dimension but I wanted my feet on the ground a little bit, even though my head might be in the clouds."

Meanwhile Sandy had discovered a love of knitting, although it wasn't the chic past-time it is today. "I had already learnt to knit and crochet from my mother and grandmother in the old fashioned way!" During her studies she saved up to buy a knitting machine, mainly knitting pieces for herself. "I really felt that I could do anything I liked in knitting. I felt there was so much potential, because you were just starting with this thread."

Sandy worked visually, drawing her designs on graph paper. She had made the connection between an individual stitch and a square on a graph paper, similar to a pixel in a digital image. And the maths was already making itself felt: "A knitted stitch is not square, unlike graph paper. Normally it's a ratio of about 2 to 3. So if I drew a circle on graph paper and tried to knit that stitch for stitch it wouldn't come out as a circle: it would come out squashed. You have to compensate using fractions and ratios." Sandy used to do this by drawing her own graph paper with the correct proportions.

"Discovering that I could invent and create things from scratch, I just took off. It seemed to be so open to creativity. I could visualise things, making the very immediate connection between a stitch and a square on the graph paper." Sandy drew and and then knitted pictures in a similar way to tapestry, using colour and textured stitches to produce three-dimensional textures.

Sandy realised that there was a huge amount of maths in textiles, such as tiling and repeat patterns. In the first machine she used you could knit automatically in two colours, with the pattern of stitches limited to an eight stitch repeat. The knitted clothes had to be designed within these limitations, though Sandy always pushed them further, such as manually overriding the machine to knit in three colours.

Punch cards were used to control Jacquard looms as early as 1801

The punch cards Sandy used to program her knitting machine had a direct relationship to those she used at university to program a mainframe computer with Fortran. In fact, this link between computing and textiles goes all the way back to the first punch cards used to control Jacquard looms in the 1800s (you can read more about early computing in Ada Lovelace — visions of today).

Sandy had found the way to combine her scientific and artistic sides: "It just sort of seemed to make so much sense to me. And I knew, while I was half way through my maths course, that this was what I wanted to do. So that was a great discovery." Sandy finished her maths degree, and started her own knitwear design business.

Building the business

Starting off with selling soft furnishings in UK department stores, such as a play rug that resembled a garden, Sandy also did one-off commissions. As her work became well-known she was asked to create pieces for magazines, television and theatre, such as some of the costumes for the very first production of the Cats musical. When Cortelle wanted to promote a new range of yarns, Sandy depicted the history of the Universe in 26 feet of knitting!

Tranquil vale, designed by Sandy Black

Sandy's pieces moved between geometric patterns and some that were highly asymmetric and non repeating. Often they were like pictures, that wrapped around the body, where she "used the body as a canvas".

"I was very inspired by landscape, skies and textures and so on. And I'd make the pattern work all the way around the body. So you'd have a shape and I'd really work hard to make sure it all matched up even though it was made in separate pieces." This came down to careful planning and understanding of how the knitted two-dimensional pieces would join together and hang on the body.

This sort of design leads to very complicated patterns, and once Sandy was designing fashion ranges rather than one-off commissions she had to design her patterns for a range of body sizes. "If something was a very complicated pattern and I'd made it so that it all matched, you couldn't then make it a little bit bigger here and there." Instead, she would often adjust the tension of the knitting to create larger or smaller sizes.

Tension in knitting means how tightly packed the stitches are within the fabric. In a knitting pattern the density of stitches is indicated by the number of stitches and rows that should be in a standard area: for example "22 stitches and 30 rows = 10 cm square measured over stocking stitch on 4mm needles" (see Learn2Knit for more information). If your tension is too loose, and your 22 stitches and 30 rows fill an area larger than 10 cm square, then your final knitted garment will end up larger. Alternatively if your tension is too tight and your area is smaller, your garment will end up too small. Tension can be adjusted by using different sized needles for hand knitting, and knitting machines can be set to knit at different tensions.

Squares knitted at different tensions by using differently sized needles, but
all have the same number of rows and stitches [Image from The Purl Bee,
reprinted with permission]

"The maths came in in all sorts of ways. Because not only was I doing the designing and organising the production, I initially used to do my own VAT returns!" Sandy was also involved in adult education, teaching numeracy part-time, while she built up her knitwear business. "It was at the time of metrication [when metric units such as grams, litres and metres were replacing pounds, ounces and yards] and there was a lot of confusion. We were finding ways to help people understand what had passed them by at school. But people had fantastic ways to cope, to find things out and to calculate. Our approach was to reinforce that, to show that there wasn't one right method."

"My colleague Diana Coben, who is now a Professor of Numeracy at the King's College London, and I developed our own materials. The worksheets we developed were eventually published by the Inner London Education Authority and then by the Adult Learning and Basic Literacy Skills Unit. It's still in print, called the Numeracy Pack, and its four books of worksheets, that we updated only two or three years ago, are in the 4th edition!"

Over the next 15 years Sandy built up an international business, showing and selling her work in countries such as Japan. "It's quite a tough world to be in, and fashion doesn't attract investment very easily. It's a very difficult business because you have to invest in your designs and your sample range, you have to show it, you have to get your orders and then produce them, which means you have to buy your materials, pay your people to make them, and eventually deliver them. And eventually some time, maybe 9 months later, perhaps get some money, if they paid you!"

In the late 1980s Sandy decided to scale back, and ran a mail-order business focusing on knitting yarns and knitting kits rather than the ready-to-wear. "I was a pioneer of knitting kits and I also produced my own yarns. I became known for slightly thicker yarns, mohair (which wasn't being used a lot) and hairy yarns like angora." Sandy also started teaching knitwear design at the University of Brighton, eventually working full time as Head of Fashion and Textiles.

The shape of things to come

Now Sandy is Professor of Fashion and Textile Design at the London College of Fashion, where she is the director of the Centre for Fashion Science. "I started off by saying I like to join the dots. It goes right back to my education, when I had to separate my interests between art and the creative visual side and the logical side of the sciences. And now in this fantastic programme we can apply emerging science and technology into textile development and fashion development."

One of the key themes of the research is how science and technology can create fashion that improves our lives. "Fashion is quite endemically wasteful. We want fashion, we want renewal, and it is a major industry. So instead of stopping fashion we want to do things a little bit differently. Perhaps we can harness science and technology and engineering to create things that last a bit longer or perhaps have more multifunctionality."

Wonderland: the dress dissolves into a gel
that can be used to grow plants

There are a number of research projects at the Centre. One project uses 3D body-scanning to obtain an individual's dimensions, and then takes these right through the manufacturing process to create clothing perfectly fitted to that person. Another project, called Wonderland, uses unusual materials, creating beautiful plastic dresses that dissolve in water to form a gel that can be used to grow plants. The aim is to highlight plastic waste, and perhaps the technology might lead to a better use of empty plastic water bottles.

Sandy's own research is focused on three-dimensional seamless garments. This sounds incredibly futuristic, but in fact we all have a drawer full of examples. "A sock is a fantastic thing, it's a great piece of engineering if you think about it. It's a tube that bends in the middle, very efficiently using the material to make the sock heel." Socks are knitted as a circle starting at the top, and then the shape is created by adding or removing stitches. "If you bent a solid tube you'd have a wasted bit of material, that isn't elegant. Whereas in knitting you can do that and it's very elegant. Because you are controlling, engineering, the number of stitches."

The image of controlling the shape of a surface conjures up mathematical ideas of topology. In fact Sandy has written papers on topology and knitting, and hopes to do more of that with her research. "I've installed the latest technology in order to do some of the seamless knitting automatically. Gloves are one of the key thing — we take them for granted but to actually cover that shape with one piece of fabric is fantastic."

Close up of crocheted Lorenz manifold

The techniques of fashion are opening up new ways to illustrate mathematical concepts. A recent well-publicised example was the Lorenz manifold crocheted by Hinke Osinga and Bernd Krauskopf, which was reported in Plus. "That is just fantastic. It's making a connection. Crochet is a three dimensional activity and it's incredibly flexible," says Sandy. In some ways the physical realisation of the crocheted manifold gave people a tangible understanding of a very esoteric concept. You could see the formation of the surface through the stitches, giving a sense of the curvature and shape that might be hard to take in even from advanced computer images. "They were able to make it absolutely accurate. There was a real correlation between the number of stitches and the way it is made mathematically."

So what advice does Sandy have for aspiring designers, or for anyone struggling to combine their creative and scientific sides? "Nobody told me I would have a career in knitting. It wasn't an obvious option, but it was something that spoke to me. I think people have to really listen to themselves, follow their instincts and put together something that is quite personal. I think anything is possible."

About the author

Sandy Black was interviewed by Rachel Thomas, Co-Editor of Plus, in London in November 2009.