Something about nature loves a helix, the ubiquitous spiral shape taken on by DNA and many other molecules found in the cells of living creatures. Now physicists Randall Kamien and Yehuda Snir, from University of Pennsylvania, may have a mathematical answer to why this shape is so common in nature.
"The classic answer is that helices are helical because the shape is dictated by bonds between molecules. But that only answers how a helix is formed and not why they are that shape," said Kamien, a professor in Penn Department of Astronomy and Physics. "It turns out that a helix, essentially, is a great way to bunch up a very long molecule, such as DNA, in a crowded place, such as a cell."
Kamien and Snir modelled the contents of a cell as a solid tube in a solution of hard spheres (the tubes could represent parts of proteins and the spheres other molecules in the cell). As far as the spheres are concerned, the tube not only takes up the space it occupies in the cell, but also excludes them from being in a region around the tube that is dependent on the size of the spheres. This reduction in space increases the energy of the arrangement - the more "squashed" they are, the higher the energy. But in nature things tend to the have the lowest energy possible. By bending the tube into a helix (actually, the tube is bent so that it is centred on a helix curve), the amount of space denied to the spheres is reduced, as the excluded region begins to overlap on the turns. But there is a balancing act between the energy going in to bending the tube, and the energy released by giving the spheres more space, and this balance is affected by the relative sizes and geometries of the spheres and tube.
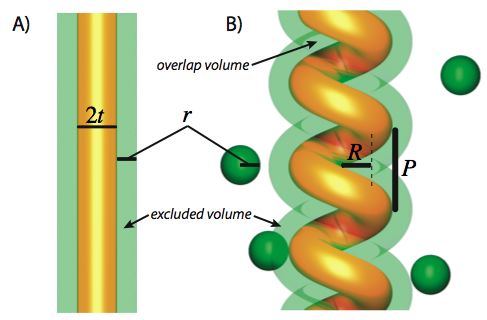
The tube (with radius t) actually excludes the spheres (with radius r) from a cylindrical
region of space with radius t+r (Figure A).
However as the tube bends into a helix, the excluded region outside the tube overlaps
on the bend, and reducing the size of the excluded volume (Figure B).
(Image reprinted with permission from Snir and Kamien, SCIENCE 307:1067 (2005).
Copyright 2005 AAAS.)
The researchers used this interaction of the spheres with the tubes, balancing the energy within the system, as a surrogate for the tight confines of the cell. Previous work published in Nature in 2000 suggested that, even without the spheres, in the confined environment of the cell the tubes would form helices with a particular geometry defined by their radius (R) and pitch (P - the distance between two points exactly one rotation apart on the helix). So, in Kamien and Snir's model, if the spheres are very small, the tube will bend into a helix with a pitch-to-radius ratio P/R = 2.5. Although this result has come entirely from a mathematical argument (which can also be used to study knot theory, finding optimal knots in the sense that they use the shortest amount of string), it closely agrees with the pitch-to-radius ratio found in models of real proteins.
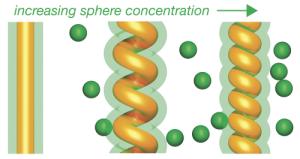
As the cell becomes more crowded, the tube is bent into a tighter and tighter helix (Image by Randall D. Kamien)
However, as the spheres grow very large, this optimal pitch-to-radius ratio decreases and tends towards zero, and the tube unwinds to become straight. And if the spheres are neither very large nor very small compated to the tube, as the concentration of spheres increases - as the cell becomes more crowded - the tube is again bent to form a helix, as the energy from interacting with the spheres as the tube takes up more space overcomes the energy needed to bend the tube.
The researchers say that their result suggests a mathematical explanation for the helices found in many situations in biology, such as at the onset of protein folding. "It would seem that the success of the helix as a shape in biological molecules is a case of nature working the best it can with the constraints at hand," Kamien said. "The spiral shape of DNA is dictated by the space available in a cell much like the way the shape of a spiral staircase is dictated by the size of an apartment."