Myths of maths: The golden ratio
This article is based on a talk in an ongoing Gresham College lecture series. You can see a video of the talk below.
Most of you will have heard about the number called the golden ratio. It appears, for example, in the book/film The da Vinci Code and in many articles, books, and school projects, which aim to show how mathematics is important in the real world. It has been described by many authors (including the writer of the da Vinci Code) as the basis of all of the beautiful patterns in nature and it is sometimes referred to as the divine proportion. It is claimed that much of art and architecture contains features in proportions given by the golden ratio. For example it is claimed that both the Parthenon and the pyramids are in this proportion. It has also been claimed that the golden ratio appears in the human body, for example as the ratio of the height of an adult to the height of their navel, or of the length of the forearm to that of the hand.
Yet in my whole career of applying mathematics to the real world I have come across the golden ratio exactly twice. Yes, twice! So are any of these great claims made for the golden ratio true?
What's the golden ratio again?
Let's start by quickly recalling what the golden ratio actually is. It was defined by the ancient Greek mathematician Euclid as follows. Imagine you have a line segment which you would like to divide into two pieces. You'd like to divide it in such a way that the ratio between the whole segment and the longer of the two pieces is the same as the ratio between the longer of the two pieces and the shorter one. What should this ratio be?

We'd like to choose A and B so that (A+B)/A=A/B.
A bit of maths (see here) will reveal that the ratio should be
![\[ \phi = \frac{1+\sqrt{5}}{2}\approx 1.618. \]](/MI/bec836b6d6beb601263198e8affc4444/images/img-0001.png) |
The fact that 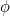 is defined as a ratio between two lengths means that you can look for it whenever you are looking at something that has segments of lines in it - whether that's a face or a building.
is defined as a ratio between two lengths means that you can look for it whenever you are looking at something that has segments of lines in it - whether that's a face or a building.
The golden ratio in the human body
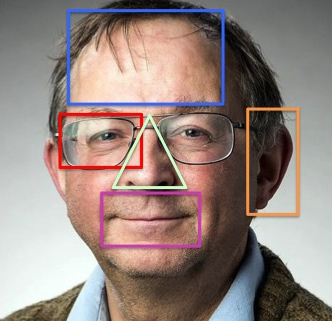
The golden ratio is supposed to be at the heart of many of the proportions in the human body. These include the shape of the perfect face and also the ratio of the height of the navel to the height of the body. Indeed, it is claimed that just about every proportion of the perfect human face has a link to the golden ratio (see this article to find out more about such claims).
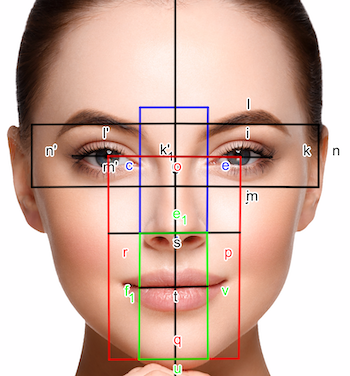
You can superimpose all sorts of rectangles on a beautiful face and then claim that beauty derives from the proportions of the rectangle.
However, none of this is true, not even remotely. The body has many possible ratios, lots of which lie somewhere between 1 and 2. If you consider enough of them then you are bound to get numbers close to the value of the golden ratio (around 1.618). This is especially true if the things that you are measuring are not particularly well-defined (as in the picture on the left) and it is possible to vary the definition in such a way as to get the proportions that you want to find.
If you look hard enough you will also find proportions in the human body close to 1.6, 5/3, 3/2, the square root of 2, 42/26, etc, etc. Indeed most numbers between 1 and 2 will have two parts of the body approximating them in ratio. Similar spurious patterns are also observed in the solar system (which also has lots of different ratios that you can choose from). Also remember that as the golden ratio is an irrational number (see below) you will never see it exactly in any measurement.
All of this is an example of the way that the human brain finds spurious correlations. Indeed given enough data it is possible to find patterns that agree with almost any hypothesis. A good way to see this is to go outside on a nice sunny day and look at the clouds. Sooner or later you will find a cloud, which fits some novel pattern. As an example look at this BBC News article reporting on a "warrior queen" having been observed in a cloud pattern.
This phenomenon can actually be quite dangerous, when spurious correlations are found in data to prove a point. For example they can lead to false accusations and even to false convictions. For a lot of examples of spurious correlations see this website.
Spirals, golden and otherwise
If you take a line divided into two segments 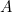 and
and 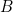 so that
so that 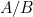 is the golden ratio, and then form a rectangle with sides
is the golden ratio, and then form a rectangle with sides 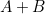 and
and  , then this rectangle is called a golden rectangle.
, then this rectangle is called a golden rectangle.
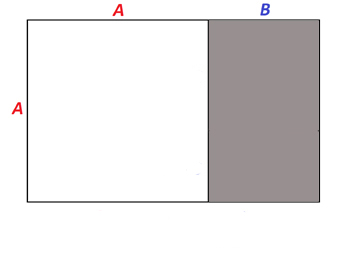
A golden rectangle is made up of a square (white) and a smaller rectangle (grey). The smaller rectangle is also a golden rectangle.
The golden rectangle we have just formed consists of a square and a smaller rectangle, which is itself a golden rectangle (see here to find out more). This golden rectangle again consists of a square and a smaller rectangle, which is itself a golden rectangle. And so on.
Using the sequence of smaller and smaller golden rectangles we can form what looks like a spiral. Simply draw a quarter circle into each of the squares that appear in the golden rectangles.
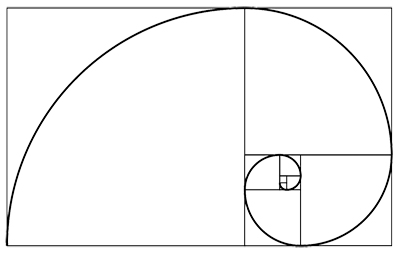
A spiral shape constructed from the golden rectangle.
It is often claimed that this spiral-like shape can be found in many places in in nature and art. For example, as the shape of a nautilus shell, the shape of a galaxy, the shape of a hurricane or even of a wave.
There are two problems here. Firstly, the shape isn't a spiral. It is a sequence of circular arcs. As you go from one arc to another the curvature of the spiral jumps. It is most unlikely that in any natural phenomenon we would see such jumps. In fact, the shape is only an approximation to a true spiral. The form of spiral that it approximates is an example of a logarithmic spiral. Such spirals are very common in nature. They have the polar equation
![\[ r =a e^{b\theta }, \]](/MI/ab5c7eed4c794ae3d2257d88acab2fe7/images/img-0001.png) |
 is the base of the natural logarithm. In nature we see such spirals everywhere, with different values of
is the base of the natural logarithm. In nature we see such spirals everywhere, with different values of  and
and 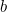 depending on the context. The reason these spirals are so common is that they have the property of self-similarity. This means that if you rotate the spiral by any fixed angle then you get a spiral which is a rescaling of the original.
depending on the context. The reason these spirals are so common is that they have the property of self-similarity. This means that if you rotate the spiral by any fixed angle then you get a spiral which is a rescaling of the original.
The so-called golden spiral has the particular value of 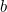 ,
,
![\[ b=\frac{\ln {\phi }}{(\pi /2)}=0.3063489... \]](/MI/9cf89760c1bbf8c13c7dea9304ac15c2/images/img-0001.png) |
where 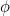 is the golden ratio (and angles are measured in radians).
is the golden ratio (and angles are measured in radians).
There is no reason at all why this number is in any way special. The nautilus shell is a logarithmic spiral because the self-similarity property allows the shell to grow without changing shape. The values of 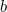 observed for the nautilus shell bear no relation to value above, with the value of
observed for the nautilus shell bear no relation to value above, with the value of 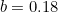 seen most commonly in actual shells.
seen most commonly in actual shells.
Art and architecture
We have to be careful here. It is certainly true that some artists, such as le Corbusier (in his Modulor system), have deliberately used the golden ratio in their art work. This is because it has been claimed that the proportions of the golden rectangle are particularly pleasing to the human eye, and that aesthetically we prefer the golden rectangle to all other rectangles. Thus it makes sense to use them in art works. It is then claimed that the golden ratio can be seen in just about every other work of art and architecture.
The evidence for the golden rectangle being especially pleasing is pretty thin. Psychological studies showing different rectangles to groups of people seem to indicate that there was a wide range of preferences, with the ratio of the square root of two to one often being preferred over others. Test yourself on the rectangles below to see which you prefer.

According to Keith Devlin's book Devlin's angle: The myth that won't go away, the idea that the golden ratio has any relationship to aesthetics at all comes primarily from two people, of which one was misquoted, and the other resorted to invention. The misquoted author was Luca Pacioli, who wrote a book called De Divina Proportione back in 1509. The book was named after the golden ratio, but didn't argue for a theory of aesthetics based on the golden ratio, or that it should be applied to art and architecture. Such a view was misattributed to Pacioli in 1799.
Pacioli was close friends with Leonardo da Vinci and it is often claimed that Leonardo himself used the golden ratio in his paintings. There is no direct evidence of this. Perhaps the most famous of these examples is the Vitruvian Man. However the proportions in this painting do not match the golden ratio. Indeed Leonardo only mentioned whole number ratios in his works. Supposed examples of the golden ratio appearing in his pictures are in the same class as those finding the ratio in nature.
Devlin attributes the "popularisation" of the golden ratio to Adolf Zeising, a 19th century German psychologist who argued that the golden ratio was a universal law that described "beauty and completeness in the realms of both nature and art [...] which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical." This was simply an example (as above) of seeing spurious patterns. However, Zeising's work went on to influence many others, and laid the foundations for much of the modern myth.

The so-called golden spiral superimposed on the Parthenon. There is no evidence that the golden ratio played a role in the design of this building. Underlying image of the Parthenon: Oyvind Solstad, CC BY 2.0.
Another example of this myth is the claim that the golden ratio appears in the proportions of the Parthenon, part of the Acropolis in Athens.
There is no evidence of this in Greek scholarship, and the idea that the Parthenon has proportions given by the golden ratio only dates back to the 1850s. Furthermore, the actual measurements of the Parthenon do not give proportions especially close to the golden ratio, unless you are careful with your choice of rectangles. In fact, the Parthenon takes its harmonious appearance from the clever deployment of lines that look parallel but in fact converge or curve, so it's virtually impossible to take measurements precise enough to give exact ratios. As the proportions of the Parthenon vary with its height it is simply not possible to find an overall proportion that agrees with the golden ratio.
The same applies to the rest of Greek architecture: there is no evidence whatsoever that the Greeks considered the golden ratio aesthetically pleasing, or used it in their art and architecture at all.
It also applies to music. It is claimed that the golden ratio is important in musical composition. There is little evidence of this. However what is important in composition is the scale, and the scale is very closely linked to the twelfth root of 2. It is this latter number which lies at the heart of music, not the golden ratio [reference}.
There is very real danger in these persistent myths about the golden ratio. School children and many others are being duped into a false reality about the way that maths works. Sooner or later they will find that this reality is untrue, and will lose faith in the very real ability of maths to explain the world.
The great reality
Having been rather dismissive about the golden ratio I would like to conclude this section by stressing just how amazing a number the golden ratio really is - it really doesn't need all those spurious claims to make it special.
First, let's turn to natural phenomena that really are related to the golden ratio. The golden ratio is intimately related to the famous Fibonacci sequence
![\[ 1,1,2,3,5,8,13,21,... \]](/MI/bfa464bc3f1681e856b96d3b13a0cc3b/images/img-0001.png) |
You can find out more about this link here. The Fibonacci sequence certainly does appear in nature as it is both linked to the way that populations grow, and also to the way that shapes can be fitted together. For example, the sequence can be seen in the spirals on sun flowers which have to fit together in an ordered fashion, and in the leaves on some plants that need to be arranged to capture the most sunlight. As a result it is possible to observe ratios close to the golden ratio arising in certain natural phenomena (find out more here).
These phenomena include the distribution of drones to female bees in a bee-hive, which is linked to the way that bees reproduce over many generations (find out more here). So it is indeed possible to see the golden ratio in the garden, and there are very good mathematical reasons for this.

Fibonacci thought of his sequence when considering the population growth of idealised rabbits. See this article to find out more.
But perhaps even more interesting are the many fascinating mathematical properties of the golden ratio. These are explored in various Plus articles, but I would like to point out one that is particularly fascinating and which really sets the golden ratio apart from other numbers: its extreme irrationality.
Irrational numbers are numbers that can't be represented by fractions and that have an infinite decimal expansion that doesn't end in a repeating block. This very fact means that it is hard to observe irrational numbers in nature. The golden ratio has the amazing property of being the most irrational number of them all. This means that not only is it not possible to represent it exactly as a fraction, it isn't even possible to approximate it easily by a fraction. See this article for the mathematical details.
The difficulty of approximating the golden ratio by a fraction makes it a very useful number to mathematicians and scientists studying the process of synchronisation. This occurs when a system with a natural frequency is forced by one of a different frequency, and adopts the forcing frequency. One example is the synchronisation of the human body to the daily frequency of sunlight. A second example is the Earth's climate which synchronises to the natural cycles of the orbit around the Sun.
However, synchronisation can itself be a problem, leading to unwanted resonances in a system (such as a suspension bridge vibrating severely if a marching band walks over it). By choosing two frequencies in the ratio of 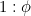 we can avoid synchronisation due to the extreme irrationality of the golden ratio. This very useful property appears to be exploited by the brain and insect species as well as climate scientists and even people who manufacture aircraft.
we can avoid synchronisation due to the extreme irrationality of the golden ratio. This very useful property appears to be exploited by the brain and insect species as well as climate scientists and even people who manufacture aircraft.
So the golden ratio does have a starring role, but not one that you often read about in the mythology associated with it. This is a great pity! It is a lovely paradox that the most interesting thing about the golden ratio is that it isn't a ratio.
About the author
Chris Budd.
This article is based on a talk in Budd's ongoing Gresham College lecture series (see video above). You can see other articles based on the talk here.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.