At a recent maths conference on the impacts of climate change on the human environment, I met a researcher whose current project was to "model Dorset". When I pressed them on what they meant by this, they said that they were trying to model how the tourist industry and associated local businesses in Dorset would be affected by possible changes in the weather and the climate.

This would involve trying to model how crowds of people would react to such events as an extreme weather situation. Naturally this proved to be a very challenging problem, but on the grounds that "some model is better than no model at all" the researcher had come to the conference to present their findings and to seek advice. (For the record I was there to talk about the more mundane subject of peat bogs.)

This project was an example of a common problem in applied mathematics: how do you model the collective behaviour of a large group of individuals? If those individuals are people, what sort of rules can we come up with to mimic the way individuals with free will can behave? This is far from an academic exercise. Many organisations rely for their operation on being able to control crowds safely and effectively. These include the police, the designers of sports stadia, London Underground, and even the Olympic Committee.

Agent based models (ABMs) provide one way of approaching this problem. In an ABM we have a number of agents (these could represent people or animals, for example) which interact with each other, and which often move under the effects of this interaction. Individual agents are typically assumed to be rational and to be acting in what they perceive as their own interest — such as reproduction, economic benefit, or social status. ABM agents may also learn from their experiences.

Most agent-based models are composed of:

• A number of agents
• A set of decision-making rules for each agent
• A set of learning rules for each agent
• A space in which the agents can move/operate and an environment in which they can interact.

Typically it's assumed that the agents' behaviour over time obeys a set of nonlinear ordinary differential equations: solving these equations will tell you where each agent will be at any given moment in time. However, the equations are much too complex to be solved by hand. Instead they are usually the subject of heavy duty computing.

The benefits of ABMs is that it is easy to change the parameters that describe the individual agents, which means that we can test, using computer simulations, how changes in the behaviour patterns of individual agents will affect the system's emerging overall behaviour. ABMs are now used widely in simulating systems in biology, sociology, economics and even management. We will now look at two examples.

Modelling a crowd of people

Some of the fundamental work on the dynamics of crowds has been done by the Swiss mathematician and sociologist Dirk Helbing and his group. Helbing makes the following assumptions about the motion of people in a crowd:

1. They have an overall goal, which may be to exit a building or to follow signage
2. They cannot walk through walls or other solid obstacles
3. They have an (individual/cultural) view on how close they may want to be to strangers
4. They will want to be close to family or friends
5. They will have a certain amount of randomness in their movements.

The crowd is then modelled as a set of agents satisfying differential equations for their movement and what Helbing called a social force model for their interactions. Let's assume that there are a total of $N$ people (agents) whom we will label $p_1$, $p_2$, $p_3$, and so on, up to $p_N$. The position of a person $p_i$ is denoted by $r_i$ and their velocity by $v_i$ (for every $i$ ranging from $1$ up to $N$). The people are then subjected to three forces. The first is a global attractive force $f_i$ acting on person $p_i$ and giving their intended motion. This motion is typically towards a target position $t_i$ at a desired speed $v^{\ast}_i$ (which may evolve with time if the person is in a hurry for example). Between any to people $p_i$ and $p_j$ there is also a repulsive/attractive force $f_{i,j}$ that drives people to avoid/come closer other people. Between a person $p_i$ and some obstacle $B$ there is a repulsive force $f_{i,B}$ causing $p_i$ to avoid $B$. For each person $p_i$ the position $r_i$ and the velocity $v_i$ obey the differential equation $$\frac{d r_i}{dt} = v_i.$$ This just reflects the fact that the rate of change of position over time equals velocity. We also have $$\frac{dv_i}{dt} = f_i+f_{i,j}+f_{i,B}.$$ This reflects the fact that the rate of change of a person's position is determined by the sum of the three forces acting on them. Finally, we have $$f_i = \frac{1}{\tau_i}\left( v^{\ast}_i\frac{t_i-r_i}{|t_i-r_i|}-v_i\right),$$ where $\tau_i$ is a parameter which controls how quickly agent $i$ reacts to a social situation: a small value of $\tau_i$ means they react quickly (perhaps they don't like crowds and walk away from them quickly) and a large value means they react slowly. The equation describes how the force $f_i$, which gives a person's intended motion, depends on the distance from their target and their desired speed.

To complete the picture we also have to model the social force $f_{i,j}$. This is rather more complex to do and must take individual preferences into account. It requires information on the size and personal space preferences of each agent, and how well they can see and interact with other members of the crowd. Similar factors are used in the construction of the collision avoidance force $f_{i,B}$. The expressions for the two forces are quite complicated and I won't attempt to give them in detail here. You can find out more in this paper by Helbing and Molnar.

Does it work?

Although we are dealing with that most complex of all things, human behaviour, the crowd models do quite a good job in predicting the actual behaviour of crowds. They have now been well tested in experiments, including one memorable experiment which involved photographing undergraduates in various crowded situations, behaving as naturally as they could given that they wearing different coloured hats for easy identification. You can see reports of some of these experiments in this paper by Helbing and colleagues.

As an example of how such models work, consider two large groups of pedestrians moving in opposite directions in a corridor (this often happens in train stations, for example, as the passengers of a train disembark and meet another group trying to embark). Below we see the simulation of this using the ABM social force model. On the top we see the distribution before the pedestrians meet, and on the bottom the pattern after the two groups have interacted. As you can see, the ABM has predicted that an emergent structure has arisen, with the pedestrians organising themselves into lanes. Next time you are in a similar situation have a look and see how true this is.

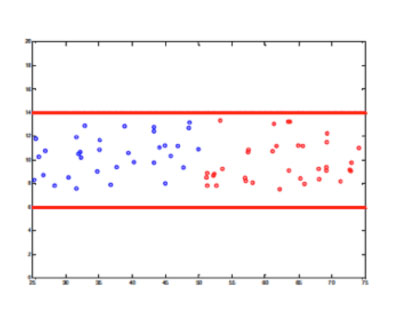
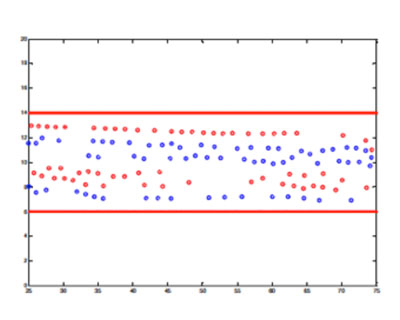
I have used these crowd models in the simulation, and design, of the lecture theatres at the University of Bath. In an earlier design of one of our lecture theatres we were faced with the prospect of over 300 students exiting a lecture theatre through a single entrance, whilst at the same time the same number of students are trying to get in. In the simulation below you can see the results, in which the two groups of students are coloured red and blue. The outcome of these computer experiments was that the door arrangements at Bath were impractical, and a new door was provided for the exiting students, which greatly eased the congestion.

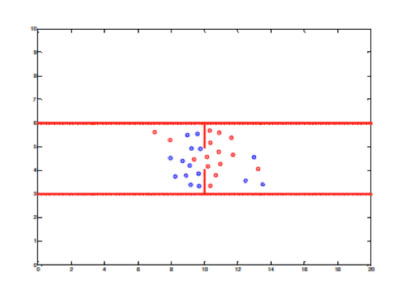
Models of crowds are now finding widespread applications. In particular they have been used to model the Olympic stadium and many other sports stadia. They are also used by the London Underground and even by the organisers of pilgrimages. The objective of these models is to find safe ways of moving large numbers of people around in both normal situations and also in emergency situations such as a fire of a terrorist attack.

A recent and very profitable use of these has been in the movie industry. For example if a director wants to simulate a huge battle (of humans, or maybe trolls, orcs and elves) then it makes sense to use an agent based model to recreate the action.

Modelling birds

It is possible to model a flock of birds (and indeed a shoal of fish) in a similar way, but with some differences. One obvious difference is that birds and fish move in three dimensions (they fly or swim), and also that they have less of a long term goal or a wish to follow signage. They also want to avoid predators. In the case of modelling a flock, the individual agents are the birds and these agents obey a set of three rules:

• Alignment: Each bird aligns its flight with the average flight direction of the local flock (the part of the flock close to it)
• Cohesion: Each bird moves towards the average position of the local flock
• Separation: Each bird tries to avoid local over-crowding and predators.

These three rules, in varying strengths, combine to give emergent complex behaviours which can be simulated using an ABM. The rules are similar in many ways to those for crowds, but have the additional features of the three-dimensional motion. The best models also include the effect of the motion of the air around the birds. If this is all included, the resulting models closely resemble actual flock behaviour. The following simulation of a flock comes from a model created by Charlotte K. Hemelrijk and Hanno Hildenbrandt in their paper Some causes of the variable shape of flocks of birds. (The movie is reproduced here under a creative commons licence.)

There is now furious activity in improving these models and applying them to many other animal species.

Where next?

As I said in the introduction, one of the problems mathematicians are faced with is that of modelling Dorset. All we have to do is to identify the agents, which in this case are the many and varied local industries, together with the local population and the tourists, factor in the weather (and the effects of climate change), and predictions of the economy and the effects of Brexit, construct the rules of interaction, light the blue touch paper and hope that we get an answer which means something useful. Well we will try at least. Watch this space.

---

---

About the author

This article is based on a talk in Budd's ongoing Gresham College lecture series (see video above). You can see other articles based on the talk here.

Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.

He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.

---

This article now forms part of our coverage of the cutting-edge research done at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.