Scientific theories need to be tested in order to be accepted as a fully fledged piece of our scientific understanding of the world around us. To do this, you need an example of your physical system that the theory describes. Your theory should make predictions about how the physcial system will behave, and so by observing your example system you can test whether the predictions of your theory play out in reality. But in order for a theory to predict how a system will behave over time, you need to know what that system looked like at the beginning of your experiment. You need to know what state it started in, something called the initial conditions.

For some theories, like Newtonian physics, these starting conditions are well known. If you want to know what happens to a ball dropped from the top of a tower, you just need to know the ball's height from the ground (and perhaps a little more information about it's shape and density and the wind conditions if you wanted to be very precise) which you can measure. You feed this information into the Newtonian equation for gravity and, assuming you're conducting your experiment on Earth, you'll find the ball falls towards Earth with an acceleration of 9.8 metres per second per second (You can read more in Constant worries). You can predict how long the ball will take to fall, its final speed, and its state at any time during its descent.

A likely starting place

For some systems though, you can't precisely know what they look like at the start. One example, says Professor Robert Wald (from the Enrico Fermi Institute, part of the University of Chicago) is a box of gas sitting on your laboratory table top. Although we can measure properties like the temperature of the gas, the volume of the box, or the pressure the gas is under within the box, we can't describe the exact state of the particles that make up the gas. It's impossible to measure the position and momentum (the mass of a particle multiplied by its velocity, meaning the momentum is a vector with both a magnitude and a direction) of each of the trillions and trillions of gas particles in the box.

Two particles of gas, each described by its position and momentum

The initial conditions of the box of gas, and indeed its state at any time in the future, is described as a point in a mathematical space called the phase space which consists of all the possible combinations of positions and moneta of all the gas particles in the box. For example, suppose your gas contains only two molecules. Then the location of each particle is given by its three spatial coordinates and the particle's momentum by its three vector coordinates. The phase space then consists of all possible 12-tuples of numbers: the first six corresponding to all the possible locations and momenta of the first molecule and the last six to all possible locations and momenta of the second molecule.

You won't know exactly which point in the phase space represents your box of gas at the start of your experiment. Instead, you can think of your box as having been randomly chosen out of all the possibilities in the phase space. This sounds hopeless, but actually, thanks to our deep understanding of how gases behave, we know how likely it is that the initial state of the gas is within a particular region of the phase space.

"There is a naturally defined probability distribution which corresponds to the probability of having the state [of the box of gas] be in some region of this phase space," says Wald. "[The probability of the state of the box of gas being in some region] is proportional to the volume of that region [of phase space], defined in some appropriate way." So in our two molecule example above, the probability of the initial condition having both molecules in one half of the box is proportional to the volume of the region in the 12-dimensional phase space that corresponds to those configurations of location.

This natural probability measure, that gives us a way to assign probabilities to regions of possible states in the phase space, allows us to assume what the initial conditions in our experiment are most likely to be. For a box of gas, this would be that the gas particles are fairly evenly spaced throughout the box, not all hiding in one corner, and that their momenta are all fairly similar, you don't have one half sitting still while the other half wizz about like mad things.

Now we have a picture of what we think our initial state of the gas is likely to be, we can apply our theory to these initial conditions and predict what will happen over time. Because we understand the physics of this system well, including knowing the probability distritbution for the initial state of the gas, the theory accurately predicts what we will see in reality.

Universal beginnings

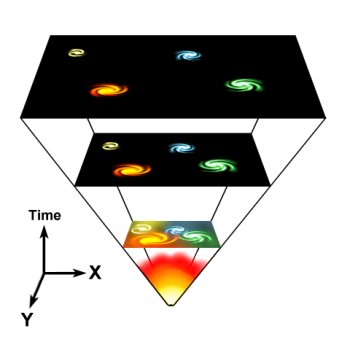
The Universe expanded from an extremely dense and hot state, but what were all the possibilities for that starting point?

Wald, however, isn't interested in studying boxes of gas. As a cosmologist he works on understanding the physics that governs the Universe: how it began, how it has changed over time and what it will look like in the future. But like the box of gas, we can't measure the initial conditions for the Universe directly. "The majority of cosmologists take the view that there was nothing special about the initial state of the Universe. But once you say that, once you say it was in some sense randomly chosen, you've got to say what all the possibilities are from where it could be chosen and what the probabilities are of those possibilities," he says. "If you want to make some predictions about what the Universe is like now, then you need to have some kind of probability distribution of what state it started in."

Unfortunately, the natural probability measure we used for the phase space for a box of gas doesn't work for cosmology. The probability the initial conditions for our box of gas was in a certain region of the phase space was proportional to the volume of that region, relative to the volume of the whole phase space at the given energy. For example, if the volume of the region in question is a third of the total volume of phase space, then the probability of the initial conditions being in that region is a third. This only makes sense if your phase space is finite.

"This doesn't work straightforwardly in cosmology for a variety of reasons," says Wald. The first reason is that for ordinary physics there is a restriction that the system has to have a finite energy overall whereas there's no such restriction in cosmology. "You have an infinite space of possibilities which has an infinite volume." So a probability measure in terms of relative volumes doesn't even make sense in terms of cosmology.

"There are many more levels of difficulty," says Wald. The Universe has many degrees of freedom (many different parameters that could vary in our models of the Universe) and it's not clear which ones are relevant and which can be safely ignored. "Even at its simplest level, defining probabilities becomes extremely problematical."

Who's watching?

There's another complication when it comes to understanding the probability distribution for the initial state of the Universe. The discussion is often dominated by the probability that observers would be around to observe the Universe in the first place. "Most of the people who talk about probabilities in terms of the initial state of the Universe [...] are talking about the probability that somewhere in this Universe there'll be observers. Then the ignorance of the probability of the initial state is largely subsumed by your ignorance of the probability of there being observers."

This leads to a whole plethora of questions: What do you mean by an observer? Do they have to be like us? Do they have to have lived in a Universe that looks a lot like ours? Perhaps you want a Universe where there are conscious beings – well, what is a conscious being? "From my point of view, the discussion degenerates very quickly into something where the input is always much greater than the output," says Wald. "What you assume arbitrarily, or by your own prejudice, always seems much greater than what you actually get out at the end."

But this doesn’t mean we should give up on trying to pin down the initial conditions of the Universe — it’s only by playing around and pursuing different ideas that we can make progress. "I think the importance of the issue and the ideas are extremely high,” says Wald. "For any of these approaches, the [chance] of making real progress is probably very low, but they could spawn new ideas that might get you somewhere. I would be very unhappy if nobody was working on this, and I'd be very unhappy if everybody was working on this and neglecting other problems." Understanding the dice that determined the starting state of our Universe is an important piece in understanding how we came to be able to ask such questions at all.

About this article

Rachel Thomas is Editor of Plus. Rachel talked to Wald at the International Philosophy of Cosmology, which took place in Tenerife in September 2014. See here for other articles and podcasts relating to the philosophy of cosmology.