Career interview: Scientific data analyst, life science technology

Gavin Harper.
Gavin first became interested in maths towards the end of his school career. "I enjoyed a wide range of subjects, but as school maths became a bit more advanced, we stopped doing routine solve-these-equations type tasks and things started getting more interesting," he says. "Solving puzzles was something I enjoyed, so maths seemed like an interesting thing to do at university." Gavin went on to do a degree in maths and statistics at the University of Edinburgh. Towards the end of the degree he developed an interest in research and decided to do a nine month diploma in mathematical statistics at the University of Cambridge, followed by a DPhil (equivalent to a PhD) in the statistics department at Oxford University.
Spotting patterns
At Oxford Gavin began his journey into biochemistry, working on a problem that at first glance doesn't appear very mathematical at all: discovering new medical drugs. Once researchers have identified the chemical processes that can cause a disease or fight its symptoms, the hunt is on to find the chemical compounds that interfere with or mimic these processes. Typically, this involves screening a vast number of candidate compounds, and it's this vastness that requires mathematical and statistical detective work. "For example, you may have a million molecules that need to be screened to see if they are active or not, for instance whether they bind to a target receptor," says Gavin. "Your screening experiment will give you a read-out telling you something about molecule activity, but the data is very noisy — it contains a lot of possibly irrelevant and imprecise information about the molecules."
It's a bit like listening to a radio with bad reception: there'll be lots of crackling, but somewhere in there is a voice telling a meaningful story. In the case of screening chemical compounds, the story is not just which of them are active and which aren't, but also whether those that are active share common characteristics that might give you more insight into the process you're looking at.
Pattern recognition in large data sets
Rather than screening molecules, let's assume you're screening people using a lifestyle questionnaire with yes/no questions such as "do you smoke?" and "are you over-weight?". For each person you get a string of 0s and 1s, where 1 means "yes" and 0 means "no". A few years later you check which of your respondents went on to develop cancer and try to spot a pattern in their answers which links the cancer to their lifestyle. For example, for four people and four questions you might get the grid:
| 1100 | cancer |
| 1110 | cancer |
| 1010 | no cancer |
| 0101 | no cancer |
It's easy to spot that people with cancer all have a 1 in the first two positions, while the people without cancer don't. With a larger data set, for example 1000 people being asked 100 questions each, you will not be able to spot a connection that easily, so you need an efficient method for comparing all combinations of digits in the sequence over all 1000 respondents.
To filter out meaningful information, you need to spot patterns within your data, just as your ear spots the familiar patterns of a human voice. This can be difficult even when your data set is small, especially if you don't know what you're looking for — just think of those "what's the next number in the sequence" exam questions. With large data sets, things get very hard very rapidly. You need a systematic method — an algorithm — for sifting through your data, classifying what you see, and spotting links. It's a mathematical task that reaches into computer science and even artificial intelligence. Mathematicians have developed a range of standard algorithms, but there's no one-size-fits-all solution. Depending on your particular problem, you need to invent something new, or adapt existing algorithms.
Maths isn't just important in interpreting the output of a screening process, but also in choosing its input. Before you start screening you'll already have some information on what kinds of molecules might turn out to be active. There are practical limitations to how many molecules you can screen, so you want to pick your molecules carefully to get a good chance of finding activity without putting all your eggs in one basket. "For example, if I think that molecule A is likely to be active, but am not sure, then picking a thousand molecules similar to molecule A would be very bad," Gavin explains. "Either the experiment tells me that, yes, it's active and there are 999 other things like it, which I already knew, or I find out that they're all inactive." So you need to balance your chance of spotting activity against what's known about the similarities between different molecules. This kind of problem — having to choose the best combination from a bewildering range of possibilities according to some constraints — turns up all over the place, from telephone routing to airline pricing, so mathematicians have developed a whole theory around it — it's called combinatorial optimisation.
Gavin's DPhil, partly sponsored by the pharmaceutical giant Glaxo Wellcome (now GlaxoSmithKline), was about improving the methods for analysing data from screening chemical compounds. His research was an interesting mix of theory and practice, getting his head around the mathematical theory behind pattern recognition, combinatorics and experimental design, and at the same time making sure that his methods were actually usable in a real lab, for example by producing efficient computer programs to analyse the experiment's output.
Gavin ended up unearthing a pattern recognition algorithm that had been developed in the 1970s, but had never been used on chemical data, and adapting it to suit his purpose. His pioneering work eventually earned him a job as the only mathematician within the computational chemistry department at GlaxoSmithKline, where he stayed for nine years.
Reading DNA
After GlaxoSmithKline, Gavin moved to his present job at Oxford Nanopore. The company is working on new technology whose main application will be to sequence DNA, the nucleic acid which makes up our genetic code.
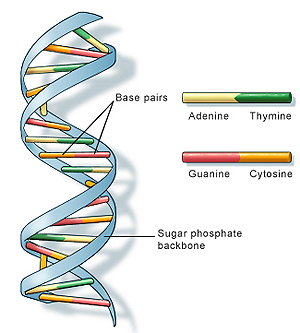
The stricture of DNA. Image: US National Library of Medicine.
DNA is made up of two strands, which curl around each other in the familiar shape of the double helix, and are linked to each other by what looks like the rungs of a ladder. You can think of each of the two strands as a string made up of four basic building blocks, called nucleotides, or bases. There are four nucleotides in DNA, adenine, guanine, thymine and cytosine, denoted by the letters A, G, T and C. The order in which these bases occur is the DNA sequence. It defines the production of proteins and therefore contains the instructions for an organism's development and functioning. There are two strands in the double helix, but the order of bases on one defines the order of bases on the other. Each nucleotide links up with its opposite number on the other strand, with adenine only bonding with thymine and guanine only bonding with cytosine. So your portion of DNA is really defined by just one sequence of A, G, T and C. Figuring out this sequence is what people mean when they talk about sequencing DNA.
Current technologies for sequencing DNA involve differently coloured fluorescent labels, which attach themselves to the different bases, each colour signalling a particular nucleotide. The hardware and reagents in this process are still complex and expensive, however prices are falling towards the cost of a full human genome being in the $10,000 to $20,000 range.
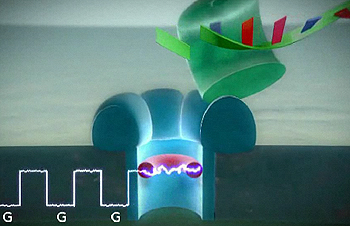
A DNA strand passing through a nanopore in a silicone chip. An enzyme, shown in green, processes the DNA strand, cleaving single bases and firing them through the nanopore. Each base then blocks an electrical signal. Image: Oxford Nanopore Technologies.
So the race is on to develop cheaper and faster sequencing technology. Oxford Nanopore are developing a technology which involves guiding DNA through nanopores — incredibly small holes 10,000 times smaller than a human hair — in a silicone chip. An enzyme feeds single bases from the end of a DNA strand through the nanopore. As each one passes through it blocks a current passing through the nanopore, creating a characteristic signature for each base. In this way the bases can be identified without expensive optical equipment, promising a lower cost system that could be scaled up using electronics. Eventually the technology platform Oxford Nanopore is developing may also be used to identify proteins in the body, both for diagnostic purposes and to discover new ones. (Watch a movie on the Oxford Nanopore website to find out more about the process.)
Mounting complexity
Maths and signal processing
Suppose you've got a scrambled audio signal. The signal might be represented by a wave form like the one shown below — how do you clean it up?
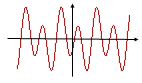
In the 19th century the mathematician Joseph Fourier realised that a periodic wave form like the one above can be broken up into simpler components which are described by the familiar sine and cosine functions. A mathematical tool called the Fourier transform does this for you. For example, you can use it to find out that the wave form above is given by the function f(x)=sin(x)+cos(x-1)-sin(x/2). You can use this information to filter meaningful information out of your signal. Fourier analysis is a staple tool in signal processing and can be used to find patterns in all kinds of information, from acoustic to visual to electrical. See below to find out more.
A faster method also means that a lot more data needs to be analysed. Each silicone chip contains hundreds of nanopores, and for each of them an electrical signal is measured and needs to be interpreted. But the signals can be noisy — how do you know which bit of the signal corresponds to which DNA base, and whether there are other parts of the DNA strand producing electrical signals that confuse the reading? Again it's a problem of pattern recognition.
To solve this particular problem, Gavin went back to an area of maths he had studied at university, and which he never thought he'd ever use again. It's called signal processing, and it provides the tools for breaking up a signal — any type of signal, from electrical to sound — into simpler components. "We are able to break the signal up into smaller chunks, to see which chunk corresponds to which base, or if there is something else in the system that's being read by the nanopore." Gavin's adaptation of these tools will not only form part of the final product the company are developing, but it's also essential in the actual development process. By assessing the clarity of the signal produced in an experiment Gavin can come up with suggestions for how the process that produced it — DNA bases passing through nanopores — might be improved to produce a clearer signal.
Generally, Gavin's ability to tackle huge data sets means that he's right there in the lab at the heart of the experimental development process. Hundreds of different experiments are run at the company labs every day, constantly evaluating potential improvements to the technology. At every experiment Gavin is there looking at the data, figuring out how it's different from other experiments that have been run, and works with the scientific team to improve the experiment.
In terms of the actual maths that's being used, it's a case of looking into the mathematical tool box Gavin equipped himself with at university and picking the right tool for the job. "You wind up using combinatorics, probability, even graph theory — an awful lot of the things you learnt as an undergraduate," he says. "It's funny how you do something as an undergraduate thinking that you'll never ever use it again, and then you suddenly turn up for work one day, scratch your head, remind yourself how it works, and then you crack on with using it."
DNA and graph theory: an example
In DNA sequencing the DNA is broken up into chunks, which are sequenced separately and then have to be re-assembled in the correct order. How can graph theory help? Here is an (over-simplified) example.
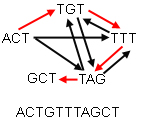
Suppose you have five chunks of the DNA sequence, each consisting of 3 letters, which you have to piece together to get the whole sequence. Each of the five chunks occurs in the entire sequence exactly once, and chunks overlap: in the whole sequence the last letter of one chunk is the first of another. For example, the two chunks AGT and TTG combine to AGTTG.
Arrange your chunks in a graph, with an arrow going from one chunk to another if the last letter of the first is the first letter of the second. Your problem is now equivalent to finding a path around your graph which visits every vertex exactly once. Such a path is called a Hamiltonian path. There are mathematical algorithms for finding Hamiltonian paths in graphs.
The figure below shows a graph consisting of five chunks. The red arrows denote a Hamiltonian path. The resulting sequence is ACTGTTTAGCT.
Communication is key
While Gavin's work involves all sorts of different areas of maths, the research that goes on at Oxford Nanopore stretches across different areas of science. There are electronic and mechanical engineers, biologists, chemists, physicists, and computer scientists. Communication is not always easy, but it's essential. There's always a hive of activity around Gavin's desk, with people from all the different groups getting an interpretation of something that's relevant to their different disciplines.
Gavin can act as a communication hub because he has a finger in every pie. He's got intimate knowledge of the experiments and the science and technology behind them, and his algorithms put him on the path to computer science. "As we're encoding our algorithms into tidy computer code for the final product, I will be talking to the guys on the computing side," he says, "I discuss the science of what's happening to them, because they're not in there with the other scientists every day. At the same time I talk to the scientists, doing exactly the opposite: discussing the limitations of the analysis and interpretation of the output. So I play the scientist to the guys doing the programming, and I play the programming guy to the people doing the science."
Communication comes naturally to Gavin, but his maths background is also a great help. "My mathematical training really helps in communicating the science to the computing group, because you need to boil a complicated experiment down to [its essential parts]. The precision of thought [that comes from mathematical training] really helps to abstract what the key elements of the experiments and the data are." Then there is also the challenge of communicating maths and statistics to the scientists. "For example, how do you present very large data sets to an audience? This is about data visualisation [— being able to present a picture, or a graph]. So I'm currently trying to develop some standard visual representation of the experiments, even though the experiments are changing, and trying to get the scientists to understand this standard representation, so that I can use it again and again."
Perhaps the most daunting aspect of Gavin's job, if you're looking in from the outside, is having to learn about completely new bits of science on the job — after all, he was never formally trained in biology or chemistry. "You're always going to move into new scientific areas within this kind of job. So there's a challenge in deciding how much you need to learn and how to extract the relevant information without getting overloaded. Personal interactions and social skills really are a key part of my job."
Traditionally, there have been few overlaps between maths and biology, and even fewer between maths and medicine. But with the advent of genetics comes not only the challenge of dealing with vast amounts of data, but also a new approach to biomedicine. We're no longer thinking in terms of one organ, one cell, or one molecule, but in terms of complex systems of interacting agents that make up an organism. Where there's complexity, you need maths, so a mathematician playing a pivotal role in a genetics company is by no means unusual. As the population scientist Joel E. Cohen put it, "Mathematics is biology's next microscope, only better."
Further reading
You can find out more about the mathematics of signal processing in the following Plus articles and podcasts:
- Catching waves: the podcast
- Saving lives: the mathematics of tomography
- Career interview: computer music researcher
- Career interview: audio software engineer
And you can find out more about the role of maths and statistics in the biomedical sciences in our ongoing project, Do you know what's good for you?
About the author
Gavin Harper was interviewed by Marianne Freiberger, Co-Editor of Plus, in March 2010.