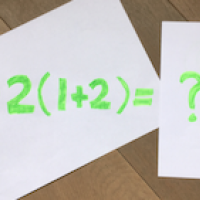
The PEMDAS Paradox

It looks trivial but it keeps going viral. What answer do you get when you calculate $6\div 2(1+2)$ ? This question has reached every corner of social media, and has had millions of people respond with two common answers: $1$ and $9$ .

You might think one half of those people are right and the other half need to check their arithmetic. But it never plays out like that; respondents on both sides defend their answers with confidence. There have been no formal mathematical publications about the problem, but a growing number of mathematicians can explain what's going on: $6\div 2(1+2)$ is not a well-defined expression.

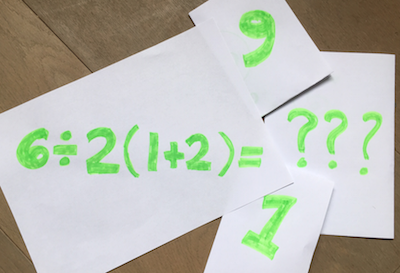
Well-defined is an important term in maths. It essentially means that a certain input always yields the same output. All maths teachers agree that $6\div (2(1+2)) = 1$ , and that $(6\div 2)(1+2) = 9$ . The extra parentheses (brackets) remove the ambiguity and those expressions are well-defined. Most other viral maths problems, such as $9-3\div 1/3 + 1$ (see here), are well-defined, with one correct answer and one (or more) common erroneous answer(s). But calculating the value of the expression $6\div 2(1+2)$ is a matter of convention. Neither answer, $1$ nor $9$ , is wrong; it depends on what you learned from your maths teacher.

The order in which to perform mathematical operations is given by the various mnemonics PEMDAS, BODMAS, BIDMAS and BEDMAS:

P (or B): first calculate the value of expressions inside any parentheses (brackets);
E (or O or I): next calculate any exponents (orders/indices);
MD (or DM): next carry out any multiplications and divisions, working from left to right;
AS: and finally carry out any additions and subtractions, working from left to right.

Two slightly different interpretations of PEMDAS (or BODMAS, etc) have been taught around the world, and the PEMDAS Paradox highlights their difference. Both sides are substantially popular and there is currently no standard for the convention worldwide. So you can stop that Twitter discussion and rest assured that each of you might be correctly remembering what you were taught – it's just that you were taught differently.

The two sides

Mechanically, the people on the "9" side – such as in the most popular YouTube video on this question – tend to calculate $6\div 2(1+2) = 6 \div 2 \times 3 = 3\times 3 = 9$ , or perhaps they write it as $6\div 2(1+2) = 6\div 2(3) = 3(3) = 9$ . People on this side tend to say that $a(b)$ can be replaced with $a\times b$ at any time. It can be reduced down to that: the teaching that " $a(b)$ is always interchangeable with $a\times b$ " determines the PEMDAS Paradox's answer to be $9$ .

On the "1" side, some people calculate $6\div 2(1+2) = 6\div 2(3) = 6\div 6 = 1$ , while others point out the distributive property, $6\div 2(1+2) = 6\div (2+4) = 6\div 6 = 1$ . The driving principle on this side is that implied multiplication via juxtaposition takes priority. This has been taught in maths classrooms around the world and is also a stated convention in some programming contexts. So here, the teaching that " $a(b)$ is always interchangeable with $(ab)$ " determines the PEMDAS Paradox answer to be $1$ .

Mathematically, it's inconsistent to simultaneously believe that $a(b)$ is interchangeable with $a\times b$ and also that $a(b)$ is interchangeable with $(ab)$ . Because then it follows that $1 = 9$ via the arguments in the preceding paragraphs. Arriving at that contradiction is logical, simply illustrating that we can't have both answers. It also illuminates the fact that neither of those interpretations are inherent to PEMDAS. Both are subtle additional rules which decide what to do with syntax oddities such as $6\div 2(1+2)$ , and so, accepting neither of them yields the formal mathematical conclusion that $6\div 2(1+2)$ is not well-defined. This is also why you can't "correct" each other in a satisfying way: your methods are logically incompatible.

So the disagreement distills down to this: Does it feel like $a(b)$ should always be interchangeable with $a\times b$ ? Or does it feel like $a(b)$ should always be interchangeable with $(ab)$ ? You can't say both.

(Image from Quora)

In practice, many mathematicians and scientists respond to the problem by saying "unclear syntax, needs more parentheses", and explain why it's ambiguous, which is essentially the correct answer. An infamous picture shows two different Casio calculators side-by-side given the input $6\div 2(1+2)$ and showing the two different answers. Though "syntax error" would arguably be the best answer a calculator should give for this problem, it's unsurprising that they try to reconcile the ambiguity, and that's ok. But for us humans, upon noting both conventions are followed by large slices of the world, we must conclude that $6\div 2(1+2)$ is currently not well-defined.

Support for both sides

It's a fact that Google, Wolfram, and many pocket calculators give the answer of 9. Calculators' answers here are of course determined by their input methods. Calculators obviously aren't the best judges for the PEMDAS Paradox. They simply reflect the current disagreement on the problem: calculator programmers are largely aware of this exact problem and already know that it's not standardised worldwide, so if maths teachers all unified on an answer, then those programmers would follow.

Consider Wolfram Alpha, the website that provides an answer engine (like a search engine, but rather than provide links to webpages, it provides answers to queries, particularly maths queries). It interprets $6\div 2(1+2)$ as $9$ , interprets $6\div 2x$ as $3x$ , and interprets $y=1/3x$ as the line through the origin with slope one-third. All three are consistent with each other in a programming sense, but the latter two feel odd to many observers. Typically if someone jots down $1/3x$ , they mean $\frac{1}{3x}$ , and if they meant to say $\frac{1}{3}x$ , they would have written $x/3$ .

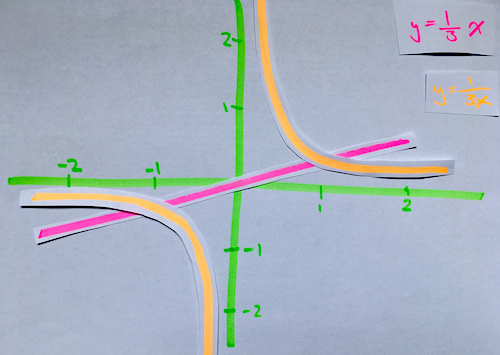
In contrast, input $y=\sin 3x$ into Wolfram Alpha and it yields the sinusoid $y=\sin (3x)$ , rather than the line through the origin with slope $\sin 3$ . This example deviates from the previous examples regarding the rule " $3x$ is interchangeable with $3\times x$ ", in favor of better capturing the obvious intent of the input. Wolfram is just an algorithm feebly trying to figure out the meaning of its sensory inputs. Kinda like our brains. Anyway, the input of $6/x3$ gets interpreted as "six over $x$ cubed", so clearly Wolfram is not the authority on rectifying ugly syntax.

On the "1" side, a recent excellent video by Jenni Gorham, a maths tutor with a degree in Physics, explains several real-world examples supporting that interpretation. She points out numerous occasions in which scientists write $a/bc$ to mean $\frac{a}{bc}$ . Indeed, you'll find abundant examples of this in chemistry, physics and maths textbooks. Ms. Gorham and I have corresponded about the PEMDAS Paradox and she endorses formally calling the problem not well-defined, while also pointing out the need for a consensus convention for the sake of calculator programming. She argues the consensus answer should be 1 since the precedence of implied multiplication by juxtaposition has been the convention in most of the world in these formal contexts.

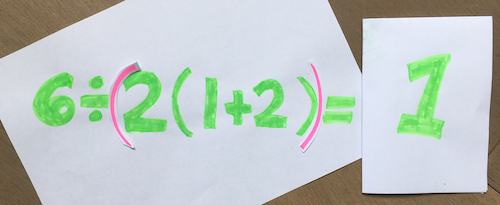
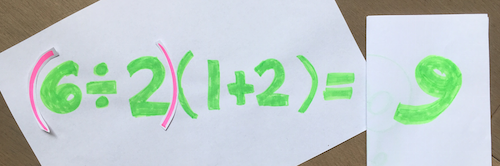
The big picture

It should be pointed out that conventions don't need to be unified. If two of my students argued over whether the least natural number is 0 or 1, I wouldn’t call either of them wrong, nor would I take issue with the lack of worldwide consensus on the matter. Wolfram knows the convention is split between two answers, and life goes on. If everyone who cares simply learns that the PEMDAS Paradox also has two popular answers (and thus itself is not a well-defined maths question), then that should be satisfactory.

Hopefully, after reading this article, it's satisfying to understand how a problem that looks so basic has uniquely lingered. In real life you should use more parentheses and avoid ambiguity. And hopefully it’s not too troubling that maths teachers worldwide appear to be split on this convention, as that’s not very rare and not really problematic, except maybe to calculator programmers.

For readers not fully satisfied with the depth of this article, perhaps my previous much longer paper won't disappoint. It goes further into detail justifying the formalities of the logical consistency of the two methods, as well as the problem's history and my experience with it.

About the author

David Linkletter

David Linkletter is a graduate student working on a PhD in Pure Mathematics at the University of Nevada, Las Vegas, in the USA. His research is in set theory - large cardinals. He also teaches undergraduate classes at UNLV; his favourite class to teach is Discrete Maths.

Add new comment

Comments

Hierarchy

My Casio calculator shows 9 when I explicit write the * sign: 6/2*(1+2) and 1 when I write the same expression with implicit multiplication: 6/2(1+2). The first case the calculation is done from "left to right", the other from "right to left", hmm...

There is no ambiguity if you do your calculation from "left to right" whenever operations have the same "hierarchical power" which is the case for multiplication and division. That's the way I learned arithmetic; and thus I join the "9-people" :-)

Hierarchy

Yes, there is no ambiguity if you (always) do your calculation from "left to right".

There is also no ambiguity if you always do multiplication before division.

You join the "9-people" because left to right has no ambiguity, but the other side has no ambiguity either.

The ambiguity arises when we have these two different rules or orders of operation and haven't agreed on which one we are going to use. It is 'ambiguous' because the writer of the expression could have meant two things and we have no way of knowing which one she/he meant.

So basically you have chosen your side arbitrarily like everyone else, unlike the actual mathematicians who had the correct answer by saying it's unclear or ambiguous.

No

No they didn't choose arbitrarily, no one is supposed to always multiply before divide. It is mentioned in the article or whatever that there are different variations of the pnemonic device that people use, such as PEMDAS, BODMAS, etc. Notice how the M and the D switch places? That's because in the case of multiplication and division, its supposed to go from left to right. 9 is right

Implied multiplication

Implied multiplication is different from explicit multiplication. It does not necessarily belong to the PEMDAS/BODMAS rules.
The article mentions that in the science textbooks a/bc means a/(bc) and this makes a lot of sense.

Teach Polish notation

By using polish or reversed polish notation this problem just disappears. it really is just a problem of semantics / (mathematical) language; and by using such a notation the ambigity just goes. Here it is in RPN:
$ dc
6 2 / 1 2 + * p
9
6 2 1 2 + * / p
1

RE: RPN

There's a reason we don't use PN/RPN every day; most tend to think in terms of direct relationships between concepts, not a concept stack that relationships operate on. Parenthesis help us read LTR while allowing nested evaluation.

Experiment:
You and I should go to the beach.
beach you I ~and~ ~go~ ~should~

Dogs and cats are like brothers and sisters.
Dogs cats ~and~ brothers sisters ~and~ ~like~

Mathematics is similar. Even many PN programming languages, such as Clojure, provide alternatives for LTR evaluation.
(+ 2 (- 4 5)) can be written as (-> 4 (- 5) (+ 2))

RPN

I took an APL course in 1979 at the University of Florida with Dr. Ralph ("Rafe") Selfridge. That was my first exposure to RPN. Though at the time I was neither a mathematics nor a comp-sci student, I really enjoyed APL and RPN. The latter came in handy when I bought an HP-48SX in the mid-'80s for use in calculus and other math classes I decided to take. I wish that little device had died on me. I found calculating using RPN much more natural than I might have expected. I'm sure that Kenneth Iverson believed it to be a wise approach to mathematical notation when he developed APL as a way to write/do/communicate mathematics and then later when the APL computer language was given life by IBM.

As for problems like the one mentioned in this article, their exfoliation online really burns my butt: my answer is to not write mathematics that no one who intended to convey an unambiguous mathematical idea would EVER write. Grouping symbols don't exactly cost extra $$ to use. :)

"Had" or "had not"?

"I wish that little device had died on me."

Did you mean to write "I wish that little device HADN'T died on me"?

David Linkletter

Incredible article and very informative, I hope to see and read more from so talented and gifted a math genius. I agree with 9.

Or...

Divide by 2 or multiply with 0.5 is the same
So...
6x0.5(1+2)
6x0.5x3=9

Well...

This actually changes the whole problem, if you were to flip the original division sign to multiplication you also have to flip the original multiplication to division so the new problem is...
6•0.5/(1+2)
which in this case gives you one

The issue is that you need more parentheses.

Not really

This only holds true if you first assume that 2(2+1) is somehow “joined”. Which is where the entire argument lies.

If you make that presumption any mathematical tool would result in the answer being 1. However, I and anyone else in the “9 camp” would argue that 2(2+1) is no different to 2 * (2+1), and similarly that there is no difference between any of the following:
6 divide 2(2+1)
6 divide 2 * 3
6 * 3 divide 2
(6*3)/2
6 * (1/2) * 3

All of these are equivalent from my perspective, and the basis for that equivalence comes from the interpretation of
“Number divide number(bracket)” as interchangeable to
“number divide number times (bracket)”
Whereas people who support 1 as the answer would interpret it as
“number divide (number times (bracket))” which I would argue is not equivalent

Division is multiplication by the inverse

6÷2 = 6×½.
6÷2(1+2) = 6×½(1+2).
The ambiguity is caused by people who prioritize implied multiplication over stated multiplication. So they are using PEiMDAS/BOiDMAS, not PEDMAS/BODMAS.
Under PEMDAS/BODMAS, implied multiplication is the same as multiplication, so:
6÷2(1+2) = 6÷2×(1+2) = 6×½(1+2), and the result of that is always 9.

Two types of multiplication?

Until this viral debate on social media I never dreamed that people could come up with the idea of defining two different kinds of multiplications: implicit (juxtapositioned) and explicit. Where the implicit multiplication has higher precedence than the explicit multiplication.
I was tought: there are four basic operators: addition, subtraction, multiplication and division. Later on, we learned that it‘s allowed to be lazy and don‘t have to write the multiplication dot. But this lazyness is pure syntactic/ typesetting sugar and doesn‘t change the order of operations. We might not write the multiplication operator but it is (from a mathematical point of view) still there. And as it‘s still there, the order of operation is applied as if it was written - order of appearence aka left to write.

So what would you say the…

So what would you say the value of 1/2π is? 0.5 * π, or 1 / (2 * π)

I believe most scientists would use the latter, i.e. they treat the justaxposed implicit multiplication as a grouping, not just a multiplication.

Polish up your maths

Polish Notation, or even better, because it emphasizes somewhat the numbers, Reverse Polish Notation, is a delight, once gotten used to. The clutter of parentheses in computation is eliminated.

Ill-formed expression

The expression 6÷ 2(1+2) is ill-formed if you want to apply PEMDAS. Consider 6/2 × (1+2). This is equally ill-formed for application of PEMDAS. Both symbols, ÷ and ×, have no context. However 6/(2(1+2))=1 has context for application of PEMDAS as does 6/2•(1+2) =9, where the dot, •, is an unambiguous separator between a rational multiplicand and a succeeding expression.

Wrong. 6/2 × (1+2) is well formed under PEMDAS.

6/2 × (1+2) according to PEMDAS:
Parentheses:
6/2 × 3
MD Multiplication/Division left to right:
3 × 3
3
Completely consistent.

Confusion

For the love of God. There is only one problem here and it is not a paradox nor is it about juxtaposition.... The only issue here is the left to right rule, a complete violation of mathematical notation we force on kids in 5th grade which DISAPPEARS in 8th grade never to be used again. The whole confusion results from this crazy rule which should never exist in the first place (parentheses! Parentheses! Never ambiguity). It is stuck in a netherworld of half consciousness, in other words some people remember left to right rule and some don't. The only problem here is our math education system which is terribly flawed.
You can see all the details on my website:
why everyone hates math. com

Brackets and ambiguity

How could we use brackets to avoid the ambiguity of a decimal expression like 1.2.3 (read out as "one point two point three)?

If the rule is that A.B means A+(B/10), then 1.(2.3) = 1+(2.3/10) = 1+(.23) 1.23

On the other hand (1.2).3 = 1.2+(3/10) = 1.2+(.3) = 1.5

6/2(1+2)

6/2(1+2)
6/2*(1+2)
By BODMAS
3*3=9

Please do read the article

Please do read the article before commenting on it!
There are two - equally correct- ways of understanding that expression, as the article points out. Restating one of them adds nothing.

The PEMDAS Paradox

In the Netherlands we learn that 12 / 3 * 2 = 8 because the rule they learned me is to divide and multiply in order of appearance. 13 - 7 + 2 = 8 and not 4 because we do it always by the rule add and subtract in order of appearance.
In order of appearance 6 / 2 (1 + 2 ) = 6 / 2 * 3 = 9 so the Casio fx-50 FH is right.

Take away the ambiguity

Why not rewrite the equation?
6
_____________
2(2+1)

Not really.

Doesn't matter how you write it, there is no ambiguity. You read and solve from left to right prioritizing according to operation rank. If you write 6/2(2+1)=6÷2×(2+1)=6÷2⋅(2+1)=
6
__ (2+1)
2
This article shows that without additional brackets, some people may chose to change the order of the operations. But choosing that approach doesn't make it true though...

Well...

We're not changing order of operations, the lack of parentheses means that we can use the distributive property to make it 6/(2+4) which simplifies to 6/6.

Hold Up

Distributive property serves no purpose here. There is no variable. The decision you are making is to see 2(1+2) as a set which means you are implying parenthesis where there are none, ie: you are implying complexity where there is none notated. If the author of the equation meant 6 ÷ (2(1+2)) they would (or should) have written it as so. Without implying complexity where none is noted the order of operations only allows for one answer: 9. That being said… it’s a poorly constructed function and that should be the real takeaway here. Math gives people the tools to be very clear of ones intention… better to use those tools and remove all possible ambiguity.

Variables versus constants

I don't understand why the distributive property is not used. Whether there are variables or constants, it should always come out the same. If we rewrite 6/2(2+1) as x/y(y+z), then distribute the y across the contents of the parentheses and come up with x/(yy+yz).

Incorrect simplification

What you have done is ignored pemdas and skipped division. x/y(y+z) would have the division done first and then you distribute the result. So distribute x/y into (y+z) to get x+zx/y. You can still distribute but it must be in the right order. Substitute back in and you get 6+1*6/2 = 9

Why does distributive…

Why does distributive property go away if there isn't a variable?

What is if it was 6÷2x where…

What is if it was 6÷2x where x = 1+2? Is that 3x or 3/x? I think most people would assume the 2 and the x are attached to each other.

Algebra is generalised Arithmetic

I agree with you and would go even further, using 2x/2x.
I think everyone with any sense of algebra would intuitively say that the answer is 1. (which then says implicit multiplication has priority over division).
Otherwise, if PEDMAS is followed to the law, we would end up with x^2 which i think very very very few people would arrive at.

Algebra

Your 2x/2x example made me remember that I lately changed my teaching habit.
I no longer write
x = (-b +- sqrt(b^2 - 4ac)) / 2a
but I write
x + (-b +- sqrt(b^2 - 4ac)) / (2a)

Algebra

I agree with your idea . . . except I think you accidentally put a + where you meant =.

Maybe the difference is subtle, but I think 9 is correct answer

The problem is that many people "glue" 2 and (2+1) together, treating it as a unity and in that way putting their relationship, in terms of priority, before the commonly accepted order of operation.

In other words, they don't treat it as:

' something...2*(2+1) ' ,

but as

' something...[2*(2+1)] ' ,

which causes the problem here.

You can't just, out of nowhere, look at '2' and '(1+2)', ignoring the relationship in which '6' is with '2', and use left-distributive property here, because you go out of the order of operations.

I think it's commonly accepted that 'xy' means 'x*y' and should be treated as such, followed by treating operation of division and multiplication with equal priority, going from left to right.

If you assume otherwise and put the priority of multiplication, even with omitted * sign, before the other operations, then you are actually and indeed making a small mistake here, assuming something that is out of convention.

So, I think that '9' is indeed the correct answer and the other way of thinking IS NOT equivalent - maybe not in obvious way, but it's disregarding the order of operations and treats unmarked 'xy' multiplication not as 'x*y', but as '(x*y)' , discretely "adding brackets"!! :-)

It should be written like 6*

It should be written like 6*(1+2)/2

No operator is the problem

People aren't "out of nowhere" gluing these together. Omitting the operator generally means that you should consider the multiplied numbers as one term. Let's change what's in the parentheses to simply "x". The problem now is 6 / 2x. Many people looking at this expression will consider 2x as one term. So they will read it as 6 / (2x), not (6/2)*x. That's the main reason why some people are in the 1-camp. No operator implies the multiplication already happened and should be taken as such as one term. Frankly it's a poorly written expression, as explained in the article.

Is 6÷2x or 6/2x where x=3…

Is 6÷2x or 6/2x where x=3 equal to 9 or 1? These are the same question. When there is a variable written like this most people attach it to the coefficient that directly proceeds it, and would consider it to be 6/(2x) or 1.

The misuse of math

Statment
6÷2×=6 X=3
6÷2times3 =? Not (2×)
Use pemdas in order
6÷2=3 3×3=6 6=6 not 6÷6=1

The Acronym used for Order of Operations

I have stopped teaching my students BEDMAS (or it's equivalents) as it is misleading in so many ways.
I now use GEMA.
One: I don't like the idea of a large MAS in someones BED!
Two: GEMA is such a lovely name.
Three: the DM (or MD) and the AS (or SA) misleads so many students.

G=Grouping
E= Exponents
M=Multiplication(and division is just inverse multiplication)
A= Addition (and subtraction is just inverse addition)

It is time we put PEDMAS, BIDMAS, BOMDAS, etc to BED and woke up with GEMA

I would argue that there is

I would argue that there is no answer because it is not written in any standardized form of mathematics. There is a reason why no math teacher on earth would accept this as an equation, it is ambiguous. Unlike languages that can over time due to the common use of a term or word by common people, see the Oxford dictionary's inclusion of slang like ain't, mathematical notation can only change by the agreement of scholars. Those that shout PEMAS as the answer need to learn math beyond the 4th grade. When math is used for a purpose, such as engineering, it needs to be clear and unambiguous. Proper notation allows for the identification of units of measure. We don't use "slang" math notation for a reason if it isn't agreed upon than it can become useless.

Working it like algebra

The way I see it, if there is no 'multiply' sign between the 2 and the (1+2), it acts just like if you were to have the expression 6/2x. Naturally, if x is replaced by (1+2), or (3), 2x=6, so the answer would be 1, as 6/6=1.

Truly a Paradox??

In my view, this entire article is unnecessary. Unless I'm wrong, you always solve within parenthesis first, then reset, so to speak, and go about the problem from the beginning, which in this case would place the mathematician back at the division portion. From there, you have a simple problem resembling 6/2*3=9. And you would solve it left to right to come up with the obvious answer that any online calculator I've tried comes up with; 9. Was this posted on April 1st as some elaborate joke? This is obviously 9, unless there are multiple versions of the rule of the order of operations.

Unnecessary is correct!

Unfortunately, I see it as being unnecessary in the opposite direction. Unless we have given up on the distributive method, the only way to resolve the parentheses is to expand the multiplier of 2 across the contents of the parentheses. Putting a "6/" in front of 2(2+1) does not mean that the first 2 no longer gets distributed.

You need to distribute the entire term

The entire term outside of parentheses needs to be distributed to use distributive property
6/2(2+1)
12/4+6/2
3+6
9

6/2(1+2)

Where it says “solve within parentheses first”
6/2(1+2) solve inside parentheses first
6/2(3) simplify parentheses last
6/6
Answer is 1
It doesn’t say “solve inside parentheses.”
It states “first”.

The PEMDAS Paradox - A resolution

I have spent 4 months arguing, (especially with Americans) over this matter, because they were taught differently, and in my opinion, wrongly.

At the crux of this matter are two principles that are ignored by many:
1. That multiplication is commutative, always.
2. That division is not commutative, and is only partly distributive.

Therefore, a rational person must ask themselves: when I find a math problem that involves both division and multiplication, how do I approach it, in order to retain the full power of the principles above?

Do I enter then shut the door, or do I shut the door then enter?

Do I reproduce then die, or do I die then reproduce?

That level of logic is what is missing.

Multiplication allows you (by commutation), to "walk in or out" as you wish. It allows you to "reproduce" early or late, for as long as you are alive. Once you divide, commutativity is lost (like death - reproduction is impossible afterwards).

Division, on the other hand, shuts the door; or is like the event of death. Once the door is shut, you cannot enter or leave. Once one is dead, they cannot reproduce!

How does this apply here?

Suppose we have 6 ÷ 2(2+1).
We cannot start with division, simply because it BLOCKS multiplication from being commutative.

You see, clearly, 2*(2+1) = (2+1)*2 and that MUST always remain valid and feasible. We cannot prefer or apply any method that denies this principle. This should be self explanatory.

Anyone who suggests anything that denies the commutativity of multiplication opposes math itself!

So, 6 ÷ 2(2+1) can only be resolved by safeguarding the commutativity of multiplication, before we "shut the door."

That is why 6 ÷ 2(3) = 6 ÷ 6 = 1, and not 9.

We cannot ever decide to die first, then start wondering whether reproduction is possible!

Multiplication is commutative

Multiplication is commutative. a * b = b * a. The problem is how you define your variables. You assume that a = 2 and b = 3, independently of the division. The reality is, a = 6 / 2 = 3 because of PEMDAS rules. Then you have 3 * 3 (a * b) = 3 * 3 (b * a) = 9.

You can't just ignore the division and do commutation on the multiplication by itself. There's no such thing as "shutting the door", whatever that means.

Paranthesis First

Parenthesis must be solved First according to PEDMAS.
6÷2(2+1)=6÷2(3)=6÷6=1.

Wrongly solved parenthesis

6÷2(2+1)=6÷2(3)=6÷2*3=9