
The PEMDAS Paradox
It looks trivial but it keeps going viral. What answer do you get when you calculate $6\div 2(1+2)$? This question has reached every corner of social media, and has had millions of people respond with two common answers: $1$ and $9$.
You might think one half of those people are right and the other half need to check their arithmetic. But it never plays out like that; respondents on both sides defend their answers with confidence. There have been no formal mathematical publications about the problem, but a growing number of mathematicians can explain what's going on: $6\div 2(1+2)$ is not a well-defined expression.
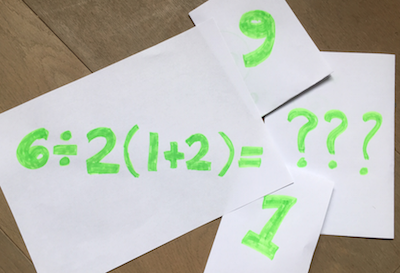
Well-defined is an important term in maths. It essentially means that a certain input always yields the same output. All maths teachers agree that $6\div (2(1+2)) = 1$, and that $(6\div 2)(1+2) = 9$. The extra parentheses (brackets) remove the ambiguity and those expressions are well-defined. Most other viral maths problems, such as $9-3\div 1/3 + 1$ (see here), are well-defined, with one correct answer and one (or more) common erroneous answer(s). But calculating the value of the expression $6\div 2(1+2)$ is a matter of convention. Neither answer, $1$ nor $9$, is wrong; it depends on what you learned from your maths teacher.
The order in which to perform mathematical operations is given by the various mnemonics PEMDAS, BODMAS, BIDMAS and BEDMAS:
- P (or B): first calculate the value of expressions inside any parentheses (brackets);
- E (or O or I): next calculate any exponents (orders/indices);
- MD (or DM): next carry out any multiplications and divisions, working from left to right;
- AS: and finally carry out any additions and subtractions, working from left to right.
Two slightly different interpretations of PEMDAS (or BODMAS, etc) have been taught around the world, and the PEMDAS Paradox highlights their difference. Both sides are substantially popular and there is currently no standard for the convention worldwide. So you can stop that Twitter discussion and rest assured that each of you might be correctly remembering what you were taught – it's just that you were taught differently.
The two sides
Mechanically, the people on the "9" side – such as in the most popular YouTube video on this question – tend to calculate $6\div 2(1+2) = 6 \div 2 \times 3 = 3\times 3 = 9$, or perhaps they write it as $6\div 2(1+2) = 6\div 2(3) = 3(3) = 9$. People on this side tend to say that $a(b)$ can be replaced with $a\times b$ at any time. It can be reduced down to that: the teaching that "$a(b)$ is always interchangeable with $a\times b$" determines the PEMDAS Paradox's answer to be $9$.
On the "1" side, some people calculate $6\div 2(1+2) = 6\div 2(3) = 6\div 6 = 1$, while others point out the distributive property, $6\div 2(1+2) = 6\div (2+4) = 6\div 6 = 1$. The driving principle on this side is that implied multiplication via juxtaposition takes priority. This has been taught in maths classrooms around the world and is also a stated convention in some programming contexts. So here, the teaching that "$a(b)$ is always interchangeable with $(ab)$" determines the PEMDAS Paradox answer to be $1$.
Mathematically, it's inconsistent to simultaneously believe that $a(b)$ is interchangeable with $a\times b$ and also that $a(b)$ is interchangeable with $(ab)$. Because then it follows that $1 = 9$ via the arguments in the preceding paragraphs. Arriving at that contradiction is logical, simply illustrating that we can't have both answers. It also illuminates the fact that neither of those interpretations are inherent to PEMDAS. Both are subtle additional rules which decide what to do with syntax oddities such as $6\div 2(1+2)$, and so, accepting neither of them yields the formal mathematical conclusion that $6\div 2(1+2)$ is not well-defined. This is also why you can't "correct" each other in a satisfying way: your methods are logically incompatible.
So the disagreement distills down to this: Does it feel like $a(b)$ should always be interchangeable with $a\times b$? Or does it feel like $a(b)$ should always be interchangeable with $(ab)$? You can't say both.

(Image from Quora)
In practice, many mathematicians and scientists respond to the problem by saying "unclear syntax, needs more parentheses", and explain why it's ambiguous, which is essentially the correct answer. An infamous picture shows two different Casio calculators side-by-side given the input $6\div 2(1+2)$ and showing the two different answers. Though "syntax error" would arguably be the best answer a calculator should give for this problem, it's unsurprising that they try to reconcile the ambiguity, and that's ok. But for us humans, upon noting both conventions are followed by large slices of the world, we must conclude that $6\div 2(1+2)$ is currently not well-defined.
Support for both sides
It's a fact that Google, Wolfram, and many pocket calculators give the answer of 9. Calculators' answers here are of course determined by their input methods. Calculators obviously aren't the best judges for the PEMDAS Paradox. They simply reflect the current disagreement on the problem: calculator programmers are largely aware of this exact problem and already know that it's not standardised worldwide, so if maths teachers all unified on an answer, then those programmers would follow.
Consider Wolfram Alpha, the website that provides an answer engine (like a search engine, but rather than provide links to webpages, it provides answers to queries, particularly maths queries). It interprets $6\div 2(1+2)$ as $9$, interprets $6\div 2x$ as $3x$, and interprets $y=1/3x$ as the line through the origin with slope one-third. All three are consistent with each other in a programming sense, but the latter two feel odd to many observers. Typically if someone jots down $1/3x$, they mean $\frac{1}{3x}$, and if they meant to say $\frac{1}{3}x$, they would have written $x/3$.
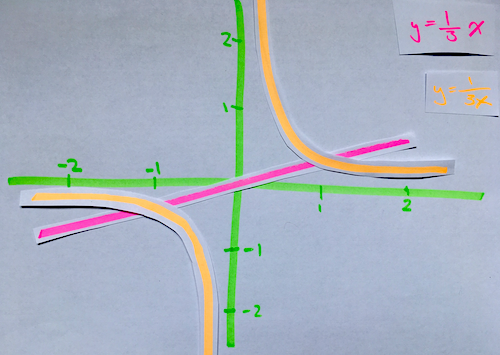
In contrast, input $y=\sin 3x$ into Wolfram Alpha and it yields the sinusoid $y=\sin (3x)$, rather than the line through the origin with slope $\sin 3$. This example deviates from the previous examples regarding the rule "$3x$ is interchangeable with $3\times x$", in favor of better capturing the obvious intent of the input. Wolfram is just an algorithm feebly trying to figure out the meaning of its sensory inputs. Kinda like our brains. Anyway, the input of $6/x3$ gets interpreted as "six over $x$ cubed", so clearly Wolfram is not the authority on rectifying ugly syntax.
On the "1" side, a recent excellent video by Jenni Gorham, a maths tutor with a degree in Physics, explains several real-world examples supporting that interpretation. She points out numerous occasions in which scientists write $a/bc$ to mean $\frac{a}{bc}$ . Indeed, you'll find abundant examples of this in chemistry, physics and maths textbooks. Ms. Gorham and I have corresponded about the PEMDAS Paradox and she endorses formally calling the problem not well-defined, while also pointing out the need for a consensus convention for the sake of calculator programming. She argues the consensus answer should be 1 since the precedence of implied multiplication by juxtaposition has been the convention in most of the world in these formal contexts.
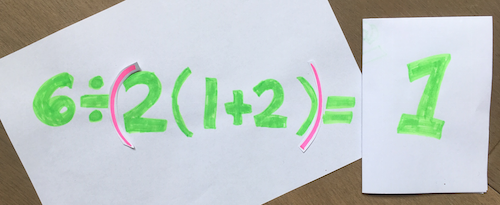
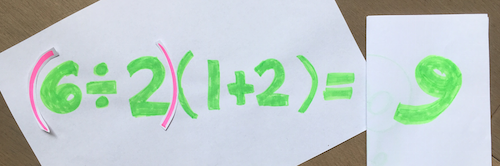
The big picture
It should be pointed out that conventions don't need to be unified. If two of my students argued over whether the least natural number is 0 or 1, I wouldn’t call either of them wrong, nor would I take issue with the lack of worldwide consensus on the matter. Wolfram knows the convention is split between two answers, and life goes on. If everyone who cares simply learns that the PEMDAS Paradox also has two popular answers (and thus itself is not a well-defined maths question), then that should be satisfactory.
Hopefully, after reading this article, it's satisfying to understand how a problem that looks so basic has uniquely lingered. In real life you should use more parentheses and avoid ambiguity. And hopefully it’s not too troubling that maths teachers worldwide appear to be split on this convention, as that’s not very rare and not really problematic, except maybe to calculator programmers.

For readers not fully satisfied with the depth of this article, perhaps my previous much longer paper won't disappoint. It goes further into detail justifying the formalities of the logical consistency of the two methods, as well as the problem's history and my experience with it.
About the author

David Linkletter
David Linkletter is a graduate student working on a PhD in Pure Mathematics at the University of Nevada, Las Vegas, in the USA. His research is in set theory - large cardinals. He also teaches undergraduate classes at UNLV; his favourite class to teach is Discrete Maths.
Comments
DerKroel
My Casio calculator shows 9 when I explicit write the * sign: 6/2*(1+2) and 1 when I write the same expression with implicit multiplication: 6/2(1+2). The first case the calculation is done from "left to right", the other from "right to left", hmm...
There is no ambiguity if you do your calculation from "left to right" whenever operations have the same "hierarchical power" which is the case for multiplication and division. That's the way I learned arithmetic; and thus I join the "9-people" :-)
Klassy
Yes, there is no ambiguity if you (always) do your calculation from "left to right".
There is also no ambiguity if you always do multiplication before division.
You join the "9-people" because left to right has no ambiguity, but the other side has no ambiguity either.
The ambiguity arises when we have these two different rules or orders of operation and haven't agreed on which one we are going to use. It is 'ambiguous' because the writer of the expression could have meant two things and we have no way of knowing which one she/he meant.
So basically you have chosen your side arbitrarily like everyone else, unlike the actual mathematicians who had the correct answer by saying it's unclear or ambiguous.
Man
No they didn't choose arbitrarily, no one is supposed to always multiply before divide. It is mentioned in the article or whatever that there are different variations of the pnemonic device that people use, such as PEMDAS, BODMAS, etc. Notice how the M and the D switch places? That's because in the case of multiplication and division, its supposed to go from left to right. 9 is right
Viktor
Implied multiplication is different from explicit multiplication. It does not necessarily belong to the PEMDAS/BODMAS rules.
The article mentions that in the science textbooks a/bc means a/(bc) and this makes a lot of sense.
Marvin Moran
Implied multiplication is simply a method for displaying multiplication sans the explicit multiplication sign, and was originally adopted to prevent the mistaking of the x multiplication symbol with the x variable. There is no inherent priority of multiplication displayed in this fashion over division or explicit multiplication. It was simply a preferable typesetting choice at the time it was adopted. It does not follow the PEMDAS BODMAS rules which is why it should not be used in arithmetic. The form a/bc actually simplifies to ac/b. However,so for those stuck on the distributive property, this expression is a/b(c+d) which by distribution simplifies to ac+ad/b. So this means 6/2(2+1) simplifies to 6*2+6*1 / 2=9 which makes a lot more sense than 6/6=1.
Marvin Moran
There is no ambiguity if you follow the order of operations. In the order of operations you do not always do multiplication before division. That is a misconception that comes from thinking that each letter of the six letter acronym equates to 1 step. It does not! There are only four steps. Multiplication and division have equal priority as do addition and subtraction. The straight order of operations represented by the acronym PEMDAS or BODMAS etc... are the current accepted standard for the solving of multi operation expressions. Particularly in regards to arithmetic operations, or expressions with purely numeric parenthesis where distribution is completely unnecessary for the resolving of the expression.
DougieH
How can the expression be ambiguous?
Ask yourself this. Does the answer 9, coming from left to right, conform with the Commutative Law?
Then see if multiplying first, conforms with the Commutative Law.
Perhaps, looking at the expression and identifying the terms, might point you in the right direction.
This is monomial division.
The TERM 6 divided by the TERM 2(1+2)
The term 2(1+2) is made up of 2 FACTORS. The factor 2 and the factor (1+2).
So with that in mind, in accordance with the Commutative Law, ab=ba, then 2(1+2) = (1+2)2, which also conforms with the Distributive Law, left distributive = right distributive. So
6/2(1+2) = 6/(1+2)2 = 1
Factors are multiplied and are single terms. Terms are added, subtracted, divided, and reciprocated.
And with reciprocation, you cannot split the factor 2 from the factor (1+2), to reciprocate. You must use the whole term to reciprocate, so
1
6*———— = 1
2(1+2)
Identify the terms and divide.
Relevant maths examples can be provided if required
John Critchley
By using polish or reversed polish notation this problem just disappears. it really is just a problem of semantics / (mathematical) language; and by using such a notation the ambigity just goes. Here it is in RPN:
$ dc
6 2 / 1 2 + * p
9
6 2 1 2 + * / p
1
TH
There's a reason we don't use PN/RPN every day; most tend to think in terms of direct relationships between concepts, not a concept stack that relationships operate on. Parenthesis help us read LTR while allowing nested evaluation.
Experiment:
You and I should go to the beach.
beach you I ~and~ ~go~ ~should~
Dogs and cats are like brothers and sisters.
Dogs cats ~and~ brothers sisters ~and~ ~like~
Mathematics is similar. Even many PN programming languages, such as Clojure, provide alternatives for LTR evaluation.
(+ 2 (- 4 5)) can be written as (-> 4 (- 5) (+ 2))
Michael Goldenberg
I took an APL course in 1979 at the University of Florida with Dr. Ralph ("Rafe") Selfridge. That was my first exposure to RPN. Though at the time I was neither a mathematics nor a comp-sci student, I really enjoyed APL and RPN. The latter came in handy when I bought an HP-48SX in the mid-'80s for use in calculus and other math classes I decided to take. I wish that little device had died on me. I found calculating using RPN much more natural than I might have expected. I'm sure that Kenneth Iverson believed it to be a wise approach to mathematical notation when he developed APL as a way to write/do/communicate mathematics and then later when the APL computer language was given life by IBM.
As for problems like the one mentioned in this article, their exfoliation online really burns my butt: my answer is to not write mathematics that no one who intended to convey an unambiguous mathematical idea would EVER write. Grouping symbols don't exactly cost extra $$ to use. :)
Captain Quirk
"I wish that little device had died on me."
Did you mean to write "I wish that little device HADN'T died on me"?
ellen birozy
Incredible article and very informative, I hope to see and read more from so talented and gifted a math genius. I agree with 9.
Jensm
Divide by 2 or multiply with 0.5 is the same
So...
6x0.5(1+2)
6x0.5x3=9
Wrice
This actually changes the whole problem, if you were to flip the original division sign to multiplication you also have to flip the original multiplication to division so the new problem is...
6•0.5/(1+2)
which in this case gives you one
The issue is that you need more parentheses.
Dylan1101
This only holds true if you first assume that 2(2+1) is somehow “joined”. Which is where the entire argument lies.
If you make that presumption any mathematical tool would result in the answer being 1. However, I and anyone else in the “9 camp” would argue that 2(2+1) is no different to 2 * (2+1), and similarly that there is no difference between any of the following:
6 divide 2(2+1)
6 divide 2 * 3
6 * 3 divide 2
(6*3)/2
6 * (1/2) * 3
All of these are equivalent from my perspective, and the basis for that equivalence comes from the interpretation of
“Number divide number(bracket)” as interchangeable to
“number divide number times (bracket)”
Whereas people who support 1 as the answer would interpret it as
“number divide (number times (bracket))” which I would argue is not equivalent
DougieH
“Assume that 2(2+1) is somehow joined”
The 2(2+1) is joined, due to it being a single term. Made up of 2 factors multiplied together. The factor 2 and the factor (2+1).
And you said “2(2+1) is no different to
2*(2+1)” and you are correct. There is no difference between them.
2*(2+1) is a single term made up of the factor 2 and the factor (2+1), and are to be multiplied.
The top 2 in your list, are correct and the answer is 1 for both.
The others have no mathematical connection to the expression.
The last example on your list, is the factor 2 being split, to reciprocate the factor 2.
That is wrong.
The full term must be reciprocated.
Relevant maths examples can be supplied if required.
Dev R.
You are on the right track when you said, "The 2(2+1) is joined, due to it being a single term."
Leibniz's Law/Substitution Property of Equality dictates:
If two quantities are equal, one can be replaced by the other in any expression or equation without altering the result's truth.
So when it is given that a=b, then anywhere in an expression that "a" appears, it can be replaced by "b," and anywhere that "b" appears, it can be replaced by "a," because they are equal and the equals sign is bidirectional.
Given: z=6, x=2 & y=3
According to Leibniz's Law/Substitution Property of Equality, when z=6, 6=z; when x=2, 2=x; when y=3, 3=y. With that being the case, 6÷2(3)=z÷xy -- and can be substituted back to numbers and vice versa an infinite number of times, since that equals sign goes in both directions.
z÷xy=?
Substituting in the numbers for the letters, one step at a time...
6÷xy
6÷2y
6÷2(3)
Every algebra textbook on the planet instructs students that terms such as xy and 2y are each a monomial, defined as one inseparable term holding a single value which is the product of its factors, formed by implied multiplication by juxtaposition (with no outer brackets necessary for it to be recognized as a monomial). In this case, xy=2(3). The term 2y is also a monomial, with 2 as its coefficient (still yielding a total combined value of the product of its factors) as 2y=2(3). Thus, xy=6 and 2y=6.
z÷xy=6÷2(3)
Calculating the value of the monomial:
xy=2(3)=6
z÷xy=6÷6=1
Any other calculation methodology violates Leibniz's Law/Substitution Property of Equality, and changes the monomial's value.
Aaron Bredon
6÷2 = 6×½.
6÷2(1+2) = 6×½(1+2).
The ambiguity is caused by people who prioritize implied multiplication over stated multiplication. So they are using PEiMDAS/BOiDMAS, not PEDMAS/BODMAS.
Under PEMDAS/BODMAS, implied multiplication is the same as multiplication, so:
6÷2(1+2) = 6÷2×(1+2) = 6×½(1+2), and the result of that is always 9.
Jörg
Until this viral debate on social media I never dreamed that people could come up with the idea of defining two different kinds of multiplications: implicit (juxtapositioned) and explicit. Where the implicit multiplication has higher precedence than the explicit multiplication.
I was tought: there are four basic operators: addition, subtraction, multiplication and division. Later on, we learned that it‘s allowed to be lazy and don‘t have to write the multiplication dot. But this lazyness is pure syntactic/ typesetting sugar and doesn‘t change the order of operations. We might not write the multiplication operator but it is (from a mathematical point of view) still there. And as it‘s still there, the order of operation is applied as if it was written - order of appearence aka left to write.
Ray
So what would you say the value of 1/2π is? 0.5 * π, or 1 / (2 * π)
I believe most scientists would use the latter, i.e. they treat the justaxposed implicit multiplication as a grouping, not just a multiplication.
Marvin Moran
Here's a grouping for you 4x. You can write it as (4x) or (4)(x), or 4*x. It doesn't much matter, they all represent multiplication. Juxtaposed implicit multiplication is just multiplication plain and simple. 1/2π is half of the value of pi. Pi being 3.14...... half of that is 1.57.... It is definitely not 1 / (2π) despite what you believe!
DougieH
1/2π is a monomial or term, made up of 2 terms, the term 1 and the term 2π.
The term 2π, is made up of 2 factors. The factor 2 and the factor π, and they are to be multiplied.
So this is 1/(2π)
Relevant maths examples can be provided if required.
Matt Garrowine
Polish Notation, or even better, because it emphasizes somewhat the numbers, Reverse Polish Notation, is a delight, once gotten used to. The clutter of parentheses in computation is eliminated.
Ghatotkacha
The expression 6÷ 2(1+2) is ill-formed if you want to apply PEMDAS. Consider 6/2 × (1+2). This is equally ill-formed for application of PEMDAS. Both symbols, ÷ and ×, have no context. However 6/(2(1+2))=1 has context for application of PEMDAS as does 6/2•(1+2) =9, where the dot, •, is an unambiguous separator between a rational multiplicand and a succeeding expression.
Aaron Bredon
6/2 × (1+2) according to PEMDAS:
Parentheses:
6/2 × 3
MD Multiplication/Division left to right:
3 × 3
3
Completely consistent.
Madamatix
For the love of God. There is only one problem here and it is not a paradox nor is it about juxtaposition.... The only issue here is the left to right rule, a complete violation of mathematical notation we force on kids in 5th grade which DISAPPEARS in 8th grade never to be used again. The whole confusion results from this crazy rule which should never exist in the first place (parentheses! Parentheses! Never ambiguity). It is stuck in a netherworld of half consciousness, in other words some people remember left to right rule and some don't. The only problem here is our math education system which is terribly flawed.
You can see all the details on my website:
why everyone hates math. com
Chris G
How could we use brackets to avoid the ambiguity of a decimal expression like 1.2.3 (read out as "one point two point three)?
If the rule is that A.B means A+(B/10), then 1.(2.3) = 1+(2.3/10) = 1+(.23) 1.23
On the other hand (1.2).3 = 1.2+(3/10) = 1.2+(.3) = 1.5
Garv
6/2(1+2)
6/2*(1+2)
By BODMAS
3*3=9
Knud Fjeldsted
Please do read the article before commenting on it!
There are two - equally correct- ways of understanding that expression, as the article points out. Restating one of them adds nothing.
John Geelen
In the Netherlands we learn that 12 / 3 * 2 = 8 because the rule they learned me is to divide and multiply in order of appearance. 13 - 7 + 2 = 8 and not 4 because we do it always by the rule add and subtract in order of appearance.
In order of appearance 6 / 2 (1 + 2 ) = 6 / 2 * 3 = 9 so the Casio fx-50 FH is right.
Marc
Why not rewrite the equation?
6
_____________
2(2+1)
E.
Doesn't matter how you write it, there is no ambiguity. You read and solve from left to right prioritizing according to operation rank. If you write 6/2(2+1)=6÷2×(2+1)=6÷2⋅(2+1)=
6
__ (2+1)
2
This article shows that without additional brackets, some people may chose to change the order of the operations. But choosing that approach doesn't make it true though...
Wrice
We're not changing order of operations, the lack of parentheses means that we can use the distributive property to make it 6/(2+4) which simplifies to 6/6.
Mr Correct
Distributive property serves no purpose here. There is no variable. The decision you are making is to see 2(1+2) as a set which means you are implying parenthesis where there are none, ie: you are implying complexity where there is none notated. If the author of the equation meant 6 ÷ (2(1+2)) they would (or should) have written it as so. Without implying complexity where none is noted the order of operations only allows for one answer: 9. That being said… it’s a poorly constructed function and that should be the real takeaway here. Math gives people the tools to be very clear of ones intention… better to use those tools and remove all possible ambiguity.
Pumpkin1
I don't understand why the distributive property is not used. Whether there are variables or constants, it should always come out the same. If we rewrite 6/2(2+1) as x/y(y+z), then distribute the y across the contents of the parentheses and come up with x/(yy+yz).
Lukie Boy
What you have done is ignored pemdas and skipped division. x/y(y+z) would have the division done first and then you distribute the result. So distribute x/y into (y+z) to get x+zx/y. You can still distribute but it must be in the right order. Substitute back in and you get 6+1*6/2 = 9
Marvin Moran
A number that multiplies a variable is a coefficient. Coefficients therefore do not exist in arithmetic because there are no variables. Algebraic parenthesis containing unlike variables cannot be added in order to be fully simplified, therefore the distributive property is used to multiply the parenthesis and consolidate all like terms in the expression bringing it to its most simplified form, so that it can be solved for a variable. When a number is juxtaposed to an algebraic parenthesis the result of the term it is part of is used to distribute multiplication over the variables in the parenthesis creating variable/coefficient pairs. These variable/coefficient pairs are the simplified terms of the parenthesis. At this point the expression is fully simplified.
In an arithmetic expression there are no variables, and therefore the parenthesis can be fully resolved to a single number which makes distribution completely unnecessary. It is simply extra steps that serve no purpose since distribution done correctly yields exactly the same results as calculating the operation in the parenthesis and multiplying the single number results without distribution!
Doug
Why does distributive property go away if there isn't a variable?
Roberto
It doesn't. He straight up made that up.
Marvin Moran
Distribution can still be used, it just isn"t necessary.
Marvin Moran
The purpose of the distributive property is to consolidate all like terms in an algebraic expression and parenthesis in order to simplify it. There are no variables in arithmetic, therefore distribution is not necessary to fully simplify the parenthesis, because they can be summed and reduced to a single number.
DougieH
There is no requirement to put parentheses round a single term.
And 2(1+2) is a single term, made up of 2 factors. The factor 2 and the factor (1+2), to be multiplied together.
And you don’t need variables to use the Distributive Law.
From the factors mentioned above, in accordance with the Commutative Law, ab=ba, we can place the factors in any order, so
6/2(1+2) = 6/(1+2)2 = 1
And to return to the original 6 we multiply the 1*2(1+2)=6
Sam
What is if it was 6÷2x where x = 1+2? Is that 3x or 3/x? I think most people would assume the 2 and the x are attached to each other.
Davo
I agree with you and would go even further, using 2x/2x.
I think everyone with any sense of algebra would intuitively say that the answer is 1. (which then says implicit multiplication has priority over division).
Otherwise, if PEDMAS is followed to the law, we would end up with x^2 which i think very very very few people would arrive at.
Jörg
Your 2x/2x example made me remember that I lately changed my teaching habit.
I no longer write
x = (-b +- sqrt(b^2 - 4ac)) / 2a
but I write
x + (-b +- sqrt(b^2 - 4ac)) / (2a)
Ken Thomas
I agree with your idea . . . except I think you accidentally put a + where you meant =.
Marvin Moran
Actually anybody following the order of operations would evaluate 2x/2x as x^2, because 2x/2x is not two separate terms, despite how it may appear to you. Math is about rules, not appearances. 2x/2x is a single term solved left to right. Terms are not separated by division, they are separated by addition and subtraction only.
Marvin Moran
You cannot apply the rules of algebra to arithmetic. There are no variables or coefficients in arithmetic. 2(1+2) is not a unit, and there is no rule in any textbook that makes it so! The 2 is not a coefficient of the parenthesis. Evaluating the parenthesis means doing the operations INSIDE the (). It does not involve any multiplication by outside numbers. Nothing outside the parenthesis is connected to it. Also this is arithmetic, not algebra. By substituting a variable for the entire parenthesis you have completely changed the expression. variables are not treated the same as numbers, because variables cannot be added to or multiplied by numbers to form single quantities. (2+1)=3. (x+y) is just (x+y) it cannot be reduced. 2(x+y) can only be simplified to 2x + 2y. it cannot be fully resolved!
Andrew M.
There most certainly are properties that cause the 2 in your example to function the same as a coefficient. Factors and coefficients are not mutually exclusive. (4*2)+(4*3), having a common factor, can be written as 4(2+3). That it is not "necessary" in arithmetic does not mean it is not "valid" in arithmetic. Similarly, distribution being "unnecessary" does not mean it is not "applicable"; it is a fundamental law in mathematics that is equally valid across arithmetic.
In the case of a disingenuous expression like 6÷2(1+2), the only way to maintain left-to-right continuity is by assuming the obelus is the automatic equivalent of a solidus in relation to the next number, which it is not. In other words, you forcibly interpret 6÷2 as 6/2 (six halves), independent of (1+2), without knowledge of whether 2 is a factor of the parenthetical.
In the end, PEMDAS, BIDMAS, etc. are not mathematical laws, rules, or properties; they are arbitrary conventions--much like language conventions that frown upon double contractions and the use (or non-use) of Oxford commas.
Marvin Moran
There is no justification for rewriting the expression, just to obtain your preferred answer. 6/2(2+1) is the written expression given. in order to obtain the answer 1, it would have to be written 6/[2(2+1)]=1 and this would also be written:
6
------- = 1
2(2+1)
However, the given expression 6/2(2+1)=9 is written:
6
--- (2+1)=9
2