Which gives a tighter fit: a square peg in a round hole or a round peg in a square hole? (The tighter fit is the one for which the ratio of peg area to hole area is greater.)
Solution
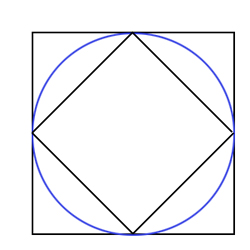
Consider the following picture:
Suppose that the side length of the large square is $a,$ so its area is $a^2.$ Then the circle has radius $a/2,$ so its area is $\pi a^2/4.$ By Pythagoras' theorem the small square has side length $\sqrt{a^2/2}$ so it's got area $a^2/2.$
The square peg in round hole fit is given by the ratio of the area of the small square to the area of the circle, which is $2/\pi.$
The round peg in square hole fit is given by the ratio of the area of the circle to the area of the large square, which is $\pi/4.$
Since $\pi > 3$ we have $\pi^2>8$ so $\pi > 8/\pi.$ Dividing by 4 gives $\pi/4 > 2/\pi$ so the round peg in a square hole gives the better fit.
Back to original puzzle
This puzzle was contributed by Colm Mulcahy, Associate Professor of Mathematics at Spelman College in Atlanta, Georgia.
Colm's own puzzles have appeared in Math Horizons and in the New York Times. He is a long-time columnist for the Mathematical Association of America and has his own blog. You can follow Colm on Twitter.
Anonymous
pi/4 > 3/4 > 2/3 > 2/pi
Anonymous
Couldn't you also consider this problem from the direction of a pressure fit?
In this case, if the height of each peg is the same then the "pressure fit" is equal for both the rectangular prism and the cylindrical hole described above.
A peg is a cylinder with a height, h. The peg would contact the sides of the square hole at the cylinder's tangents lines of length,h. Pressure = force*area. Pressure =force*(4h*negligible width of each contact line)
A rectangular prism peg with the same height, h would contact a cylindrical hole at it's 4 edges. Again the pressure would be equal. Pressure = force*4h*negligible width of each contact line.
Anonymous
A related problem which is fun, is to design a peg which fits into a triangular hole, a square hole, and a circular hole leaving no gaps.
Tim Davis
Anonymous
The entire puzzle is rendered invalid inasmuch as the puzzle asked which gives a 'tighter fit', while the answer suggested a 'better fit'. Details, details, details...
Anonymous
I thought the answer is just intuitive than mathematical: a round peg in a square hole can rotate about its axis. Whereas, a square peg in round hole cannot. (this is why manhole covers are square, though the hole itself is round)
Robertson Pon
I’ve read this 5 times and it still doesn’t make sense. Which axis are you talking about? If the z-axis, you are wrong, both can rotate. Any other, you are still wrong, neither can rotate as they are pegs.