
The beauty of maths is in the brain of the beholder
Maths is the language that explains our physical world, what the mathematician and physicist Eugene Wigner called "the unreasonable effectiveness of mathematics in the natural sciences". It is also the lightning that, sometimes unnoticed, precedes the thunder of technological innovations. Yes, mathematics serves and touches upon the advances of practically every field. Still, as a discipline unto itself, mathematics is an extraordinary example of the human pursuit of knowledge, versatile and capable of unifying areas that appear very different. The mathematician Michael F. Atiyah referred to these qualities in an address to the London Mathematical Society titled The unity of mathematics. In his own words, "The aspect of mathematics which fascinates me most is the rich interaction between its different branches, the unexpected links, the surprises, ..." .

Some visualisations of mathematical objects, like this one of the exceptional Lie group E8, are undoubtedly beautiful. But is maths by itself beautiful? (Image Jgmoxness, CC BY-SA 3.0.)
But mathematicians and mathematics aficionados also talk about the beauty of mathematics. For instance, the philosopher and mathematician Bertrand Russell affirmed that "mathematics, rightly viewed, possesses not only truth, but supreme beauty". Now, beauty is an slippery concept, much more subjective and difficult to frame than, say, applicability within maths or in other fields. To be sure, whatever beauty might be, mathematicians find an aesthetic value in the power of abstraction that mathematics has and in the connections it finds.
But how is this mathematical beauty similar to, or different from, the beauty we ascribe to a work of art? There are frequent references to mathematics as an art. In an article published in The Mathematical Intelligencer with the title Mathematics: art and science, the mathematician Armand Borel has this to say: "... mathematics is an extremely complex creation which displays so many essential traits in common with art and experimental and theoretical sciences that it has to be regarded as all three at the same time, and thus must be differentiated from all three as well."
So, as to how and why mathematics is connected to art or to other endeavours, the answer is typically ambiguous. It seems that questions of this nature are destined to remain a part of the mathematical folklore. Still, perhaps unknown to most mathematicians, something has been happening somewhere else.
A brain revolution
As early as 1909, an anatomist, Korbinian Brodmann, divided the cortex of the human brain into 47 areas, now called Brodmann areas, according to the structure and organisation of the cells. Later, as researchers began to understand the functions of different cells in the cortex, they were astounded by the fairly close relation emerging between certain Brodmann areas and the location of specific cell functions. Today, much is known about a wide range of these functions, showing the prodigious complexity of our brain. For instance, there seem to be about three thousand interconnected neurons, controlling most of our breathing and involving about 65 types of neurons!
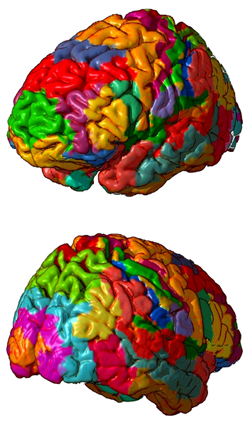
Brodmann areas in the brain.
Besides what we might call the physical functions, researchers are understanding the locations of what we might call intellectual functions. For example, an article published in 2011 in the journal NeuroImage, discussed the findings of a study locating the brain areas needed for numbers and calculations. Coincidentally, a study published the same year in the journal PLoS ONE, presented evidence towards a brain-based theory of beauty. Several studies had already shown how beauty, as related to visual, auditory and moral experience, was connected to activity observed in a specific region of what researchers call the emotional brain.
Based on all these findings, a team of two neurobiologists, Semir Zeki and John Paul Romaya, a physicist, Dionigi M. T. Benincasa, and the mathematician Michael F. Atiyah conjectured that the perception of mathematical beauty should excite the same parts of the emotional brain, roughly described by a collection of Brodmann areas. Their study, published in the journal Frontiers of human neuroscience in 2014, seems to confirm their conjecture, indeed placing mathematical beauty, as perceived by trained mathematicians, in the same areas previously identified with other manifestations of beauty.
As part of the study participants (mathematicians and non-mathematicians) were presented with sixty mathematical formulas and asked to rank them according to three categories; ugly, neutral and beautiful. The expression that was most consistently ranked as beautiful by the mathematicians was Euler's equation, $$ e^{i\pi }+1=0,$$ and the one most consistently ranked as ugly by the mathematicians was the following, extremely convoluted, formula representing the reciprocal of $\pi$ as an infinite sum: $$\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{k=0}^{\infty} \frac{(4k)! (1103 + 26390k)}{(k)!^4 396^{4k}}.$$ The formula is due to the mathematician Srinivasa Ramanujan. His collaborator Godfrey Hardy said that the formula had to be true, because no one could possibly concoct something so complicated.The choices that mathematicians made in the study seem to point to simplicity as an attribute of the mathematically beautiful.
Beauty and understanding
Although the perception of mathematical beauty might have the same characteristics, neurologically speaking, as the perception of beauty elicited by other sources, some differences remain.
To find beauty in a particular piece of music, we do not need to understand the intricacies of the composition. Likewise, we can feel the beauty of a painting or a sculpture at a "gut level", without thinking explicitly about the technical aspects.
However, the authors of the study speak at length of the difficulty of separating the perception of mathematical beauty from the understanding of the underlying mathematics. The subjects recruited for their study were sixteen postgraduate or postdoctoral students of mathematics, and twelve non-mathematicians. Among the mathematicians there was a strong correlation between understanding and perception of beauty, but it wasn't a perfect correlation: some formulas were rated ugly even though the mathematicians understood them well. Unsurprisingly, the non-mathematicians generally didn't understand the formulas very well, but they still rated some as beautiful. The authors suggest that the non-mathematician probably liked something about the formal qualities of the equations, for example their symmetrical distribution — this is something that will have to be investigated in a future study.
Finally, the tool used in this and other studies is a form of magnetic resonance imaging, fMRI, the letter f standing for "functional". The American chemist Paul Lauterbur and the English physicist Peter Mansfield were awarded the 2003 Nobel Prize in Physiology or Medicine for their development of MRI. In particular, Mansfield was credited with introducing its mathematical formalism. A nice way for our article to come full circle: the unreasonable effectiveness of maths allows us to observe our mental world and help us understand the nature of mathematics itself.
About the author

Josefina Alvarez first learnt about the study discussed in this article from a piece in the New York Times, via her husband Larry Hughes.
Josefina (Lolina) Alvarez was born in Spain. She earned a doctorate in mathematics from the University of Buenos Aires in Argentina, and is currently professor emeritus of mathematics at New Mexico State University, in the United States. Her long time interest is to communicate mathematics to general audiences. Lolina lives in Santa Fe, New Mexico with husband Larry and dog Lily. She walks every week many kilometres along the beautiful trails of Northern New Mexico. For more on her work, visit this website.
Comments
Andrew1
Great article.
David Harold Chester
John Keats (Ode to a Grecian Vase) claimed that beauty and truth are the same. Mathematics is more directly connected to truth, even if we cannot prove it to be absolute. Then due to this imperfection the comparison to beauty is rather poor and limited. What we envisage as beauty has more to do with symmetry and asymmetry of form. Indeed beauty is in the eye of the beholder and not all beholders see the same thing.
Brian Mulligan
No mention of Occam's Razor (Principle of Parsimony)? The general concept of beauty in Scientific theories applies in math as well - it's an evolutionary adaptive trait that allows us to identify the explanation of a phenomenon that is most likely to be true. Tut tut!