
Of the myriad strategems I employ to avoid useful work, the one I most enjoy is to envision how scientists of earlier eras would have made use of modern computers and what effect it would have had on the science of their times - and ours. For example, I suspect that Newton's geometrically-based arguments for particle motion would have remained essentially untouched by the hand of the machine (although Newton might well have used a relational database to trace out the various biblical lineages that seemed to have occupied most of his time). On the other hand, it's likely that Kepler would have discovered much more than his three laws of planetary motion, perhaps even anticipating Newton's equations, had he had access to a Sun or SGI workstation. And there's no doubt in my mind that Gauss would have proved the Prime Number Theorem long before de la Vallee Poussin and Hadamard if he'd been able to make use of packages like Mathematica or Maple to study the distribution of primes.
Recently, while surfing the Internet looking for some now long-forgotten item, I stumbled across a hyperlink to work of the great turn-of-the-century Scottish naturalist and polymath d'Arcy Wentworth Thompson. This serendipitous event underscored again the great advantage of search engines that are not too accurate or efficient, since the Web page that I was directed to ended up being vastly more interesting than the material I was originally trying to track down. Anyway, as any self-respecting mathematical biologist knows by now, d'Arcy Thompson's greatest contribution to theoretical biology was in the last chapter of his magisterial treatise On Growth and Form, in which he put forth a theory of biological transformations whereby one might compare the shapes of living things. What popped up on my screen that morning was nothing less than an account of what d'Arcy Thompson would have done if he'd had a computer on his worktable instead of a stack of graph paper, a ruler and a compass.
D'Arcy Thompson held a professorial chair in St. Andrews and Dundee in Scotland for the amazing period of 64 years, a record for tenure unlikely ever to be broken. Although he would write more than 300 scientific articles and books, Thompson's reputation is based primarily upon his attempts to reduce biological phenomena to mathematics in On Growth and Form. There he claimed that much about animals and plants could be understood by the laws of physics, as mirrored in the structures and patterns of mathematics. By this, Thompson displayed his essentially anti-Darwinist beliefs, at least in the sense that he would most certainly have disagreed with Theodosius Dobzhansky's well-known remark that, "nothing in biology makes any sense except in the light of evolution." Clearly, Thompson felt that a lot of biology made perfectly good sense quite outside the bounds of the principle of natural selection. Leaving aside his academic renown, Thompson seems also to have acquired a bit of a local reputation as a mild eccentric, and older folks in St. Andrews can still recall seeing him strolling about town with a parrot on his shoulder.
The novel idea Thompson set forth in On Growth and Form was to show how mathematical functions could be applied to the shape of one organism to continuously transform it into other, physically similar organisms. A famous example from his book is shown in Figure 1, in which a continuous squeezing and stretching of a rectangular Cartesian grid transforms the fish species Scarus sp. on the left to the species Pomacanthus on the right. Thompson used this same idea to show how to alter pictures of baboon skulls into skulls of other primates, as well as demonstrating how corresponding bones like the shoulder blades are related in different species.
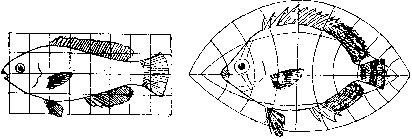
Figure 1. Two species of fish related by a continuous transformation
To a topologist, the fact that the fish species Scarus sp. can be continuously transformed into the species Pomacanthus is entirely unremarkable. This is because every organism is a closed surface, topologically speaking, and it has been known for many years what kinds of closed surfaces can and cannot be continuously mapped to each other. Speaking loosely, two such surfaces are equivalent in this sense if and only if they have the same number of "holes." Thus, considering the fact that just about all higher animals have the same number of holes for the digestive tract, ears, nostrils, and eyes, Thompson's work on biological transformations only confirms the topological fact that there exists a continuous transformation that will warp and twist the form of virtually any animal into any other one. So at first glance it doesn't seem as if there's too much "meat" in Thompson's idea, after all, since a world in which aardvarks and zebras are indistinguishable hardly seems to hold much promise for shedding light on the processes of embryology or evolution. But not so fast!
Simply knowing that there is some transformation deforming an aardvark into a zebra is a far different matter from knowing precisely which transformation(s) do the job. And if there's anything to be said for d'Arcy's view that the basic processes of evolution and development can be understood mathematically via biological transformations, then that something resides in the precise nature of the transformation. And it is to address exactly this point that I'm sure d'Arcy would have used a computer had such gadgets been available a century earlier. Fortunately, two of his successors on the faculty of the University of St. Andrews, John J. O'Connor and Edmund F. Robertson, took up this challenge and have created a program for studying the precise analytic form of these "Thompson transformations."
The program written by O'Connor and Robertson allows users to alter pictures in real time by varying parameters in mathematical functions describing the transformations, thus seeing the picture change "before their eyes" from, say, one fish to another. Figure 2 shows the program's user interface corresponding to another of d'Arcy Thompson's famous fish examples. The picture on the left, the species Argyropelecus olfersi, is mapped to the unknown species on the right by the quadratic transformation whose parameters are specified at the bottom of the screen. The reader will see from the figure that in this example the transformation only involves a linear stretching of the x and y axes, since the quadratic terms in the transformation are zero.
Symbolically, the program admits maps of the form (x, y) -> (p(x, y), q(x, y)), which take a point (x, y) of the plane on the left to the point (p, q) in the plane on the right, where p and q are polynomials of degree 2 (without constant terms) in the two variables x and y. As a result, there are a total of 10 parameters that can be varied in the process of transforming the source form on the left to any given target form on the right.
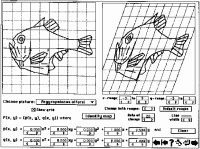
Figure 2. View of the user interface for the Thompson transformation program
Thus, with the O'Connor-Robertson program one can actually twist the 10 "knobs" independently, which corresponds to varying the 10 parameters in p and q until a particular target form is generated. Although Thompson used a wide variety of transformation, O'Connor and Robertson have discovered that most of his effects can be achieved by quadratic maps of the above sort. Consequently, by finding the parameters defining a particular quadratic map leading from one known species to another, we can hope to gain insight into the physical and evolutionary forces acting on different species. Alternately, we can also use the program to study intermediate forms like that of Figure 2, which have never before been observed - and possibly never existed.
The problem with these kinds of continuous deformations is that nothing essentially new ever turns up; by definition, there can be no discontinuous "jumps" from one species to an entirely different one via a sequence of continuous transformations. For this type of speciation to take place, we need singularities in the families of continuous transformations. While there's no room to discuss the matter further here, let me note in passing that it is to deal with precisely this situation that René Thom invented the mathematical theory of catastrophes around 30 years ago. And, in fact, Thom acknowledges his debt to d'Arcy Thompson's work, as well as to that of a later Scottish biologist, Conrad H. Waddington, in the preface to his pathbreaking work on the subject.
One set of images used by Thompson in his book was taken from work by the artist Albrecht Dürer's on facial angles. These experiments by Thompson on continuous distortions of such angles led to a wide variety of faces, calling to mind a program written a few years ago by Susan Brennan of the Hewlett-Packard Laboratories. Basically, her program is designed to continuously deform a given face in order to create a caricature of it. Serving to motivate the development of this program was the question of how humans so quickly recognize faces, even when only a few features are seen under adverse viewing conditions. Brennan hoped that her program could be used as a tool for investigating just which features people focus upon in this remarkable pattern-recognition process. The details of how the program works have been described elsewhere, but the principle is simplicity itself: Compare the target face with an "average" face, and then scale up those features that differ the most from the average face. An example of how the program caricaturizes former President Ronald Reagan is shown in Figure 3.
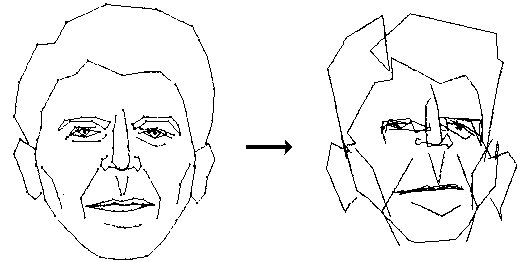
Figure 3: A computer caricature of Ronald Reagan.
Brennan has described her program as a fast way of exploring what she calls "face space." The 186 coordinates she uses to describe a target face can be thought of as the coordinates of a single point in a high-dimensional space. Since every face is a point in this same space, any two faces can be connected by a straight line in face space, each point along the line representing proportional changes in every coordinate value. The distance between any two points then serves as a measure of how similar the faces are. With d'Arcy Thompson in mind, we can also ask the computer to generate a transitional sequence from one face to another. Such a transition sequence from Elizabeth Taylor as Cleopatra to John F. Kennedy is shown in Figure 4.

Figure 4: A transitional sequence in face space.
A key factor motivating the work of both d'Arcy Thompson and Susan Brennan is to uncover invariants of the transformations from one form to another. If these transformations have any biological or psychological content at all, presumably it lies in telling us what it is exactly that allows us to recognize the caricatured version of Ronald Reagan as Ronald Reagan and not, say, JFK, or what exactly are the characteristics shared by the fish speciesScarus sp. and Pomacanthus. Only a deeper understanding of such invariants will enable us to unlock the complexity of living things. As d'Arcy himself put it, "I know that in the study of material things number, order, and position are the threefold clue to exact knowledge; and that these three, in the mathematician's hands, furnish the first outlines for a sketch of the Universe."
References
Brennan, S. "Caricature Generation: The Dynamic Exaggeration of Faces by Computer." Leonardo 18, No. 3 (1985), 170-178. (See also the account in Dewdney, K. "Facebender", in The Armchair Universe, New York: Freeman, 1988, pp. 89-99.)Rosen, R. "Dynamical Similarity and the Theory of Biological Transformations." Bulletin of Mathematical Biology, 40 (1978), 549-579.
Thom, R. Structural Stability and Morphogenesis Reading, MA: Addison-Wesley, 1975.
Thompson, d'Arcy W. On Growth and Form Cambridge: Cambridge University Press, 1917. (Dover reprint edition, 1992.)
About the author

John L. Casti is currently a member of the External Faculty of the Santa Fe Institute in Santa Fe, New Mexico, USA, where he's working on the application of biological metaphors to the mathematical modeling of problems. He edits the journals Applied Mathematics & Computation (Elsevier, New York) andComplexity, and has published a number of works of popular science such as:
- Paradigms Lost: Images of Man in the Mirror of Science (Morrow, 1989)
- Searching for Certainty: What Scientists Can Know About the Future (Morrow, 1991)
- Complexification (HarperCollins, 1994)
- Five Golden Rules: Great Theories of 20th-Century Mathematics---and Why They Matter. (John Wiley & Sons (New York) in September 1995)
- Would-Be Worlds (John Wiley)
This article was originally published in The Simply Complex column of Complexity, Vol. 1, No. 3.