Despite the name of the game, when John Conway developed the system he called Life he wasn't aiming to simulate life at all. All the same, the game's lifelike nature, with its endless complexities and unpredictabilities, has captured imaginations all over the world. Conway's original aim was entirely mathematical - he was trying to find a so-called universal system, that is, a system capable of carrying out arbitrary computations - a sort of infinitely programmable computer.
In the 1950's von Neumann, a pioneer in the field of cellular automata, succeeded in inventing a universal system. His system involved cellular automata on a two-dimensional plane, with the state of each cell at time t+1 depending only on the state of its neighbours at time t. Von Neumann's system was incredibly complicated - requiring 29 states - as a consequence of how he had derived the system. Conway describes the process von Neumann used to develop this complicated system thus: "If he wanted a certain ability, like the ability to transmit messages, he added a few more states and gave himself that ability. And if he wanted something else, he added a few more and so he got to 29 states. And the appendix to his paper is a big long list of transition tables...it's a real mess!"
By contrast, Conway's aim was to find a "spectacularly simple" universal system. Rather than explicitly forcing his system to behave in desired ways - the approach of von Neumann - he believed that the best approach was to pick a system with suitable-looking behaviour, live with it and, over time, learn how to program it to do arbitrary computations.
Is it Universal?
"For instance, take a whole lot of bits of electronics and connect them together at random in a warehouse. Then probably you have got a universal computing machine," Conway says. It's just a matter of living with the system and learning how it works. "You might press a button here and you notice that a little red light comes on, and then you try and understand how these buttons correspond to
these things and discover a way of adding two numbers. You press this button 5 times and then you do something else, and then you press it 8 times, and detect that the answer is 13. And, if the warehouse is big enough, and if the behaviour is interesting enough, you gradually learn how to use little bits of it to do whatever you like. So that's the dream. And the question now is how small can you
make the warehouse, how simple can you make the connections?"
|
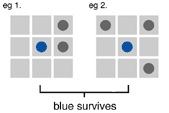
Life is played on a grid of squares where each cell is either alive (occupied) or dead (empty). You start with an initial configuration of live cells, and the game progresses through generations as the life and death rules are applied.
|
Life is not as simple as Conway had hoped, but is, he says, "a sort of pleasant failure". In one way von Neumann's system was simpler, as the state of a cell only depended on itself and its four crosswise neighbours, whereas Life involves all eight neighbours. Ideally, Conway was looking for a system that was "astonishingly simple", one that only involved one dimension - cellular automata in a line rather than in a plane. With a two-dimensional system "you have to hold the state of position (x,y) at time t. It would be much better if we could reduce the complexity of the space we are operating in", he says.
The hardest step turned out to be finding a suitable two-dimensional system to study. Although such systems operate on an infinite plane, studying them involves observing some limited finite section of the plane. Conway's research group used Go boards to develop Life, and in order to be able to study a system it was necessary that populations did not tend to explode and race off the board. This meant they had to impose some sort of death rule on the system. And of course a system would have to have sufficiently interesting behaviour in order to have any chance of being a universal system, so it was equally important that populations did not usually die out; hence, the birth rule.
"We played with all sorts of rules, studying their effects, and seeing what happened" Conway says. "Either things tended to explode in population tremendously, or else they tended to die off. So it became this question, how can you adjust the relative strengths of the birth and death rules so [that for a typical population] there is a fair probability that they won't die off, and that it doesn't grow linearly either." The real difficulty in finding a suitable system was finding the right relative strengths of these rules in order for the system to be both interesting enough to study and stable enough to live with.
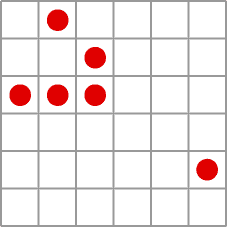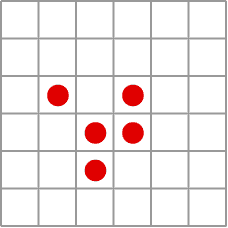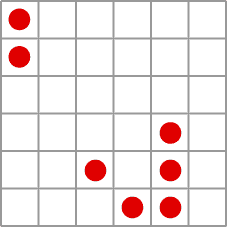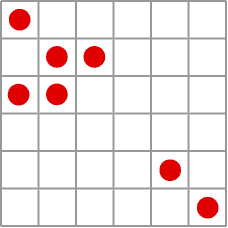
Gliders walking across the plane
Over two years of tea and coffee breaks Conway and a group of graduate students and colleagues experimented with the life and death rules. And when they arrived at the set of rules that became Life, they quickly stopped tinkering. Living with this system soon revealed the presence of configurations they decided to call "gliders" - configurations that "walked" across the plane - which was an early sign of success, because, in order to prove universality and show a system is capable of arbitrary computations, it is necessary to have some way to transmit information across the plane from one configuration to another. "When this system turned up, we totally stopped experimenting with any other rules because it was clear that this should work. It behaved in exactly the sort of way that we wanted, and we started trying to prove that it worked" Conway says.
In a matter of weeks the group had built nearly all the necessary configurations for arbitrary computations: AND gates, OR gates, and so on, just like the components of an ordinary computer. However, the one thing still missing was an initial source of gliders, which they called a "glider gun". At this point "I sort of advertised for it", says Conway. He wrote to Martin Gardner suggesting Life for his Mathematical Games column in the Scientific American and a prize of $50 was offered for a configuration whose population tended towards infinity. The column sparked the public's imagination and very quickly a glider gun was discovered by a group at MIT led by R.W. Gosper. Within two weeks of the discovery of the glider gun, both Conway's group and the group at MIT showed that the system was universal, and "it was a great success story".
Life has stimulated a huge amount of public interest ever since it was first publicised in Gardner's column. The US military at one point estimated that millions of dollars worth of computing time had been "wasted" looking at the Life game, and it still continues to be played today. Conway is pleased that Life interests the public. "I'm always trying to sell mathematics to the general public, to turn them on" he says. And perhaps it was lucky that Conway developed a two-dimensional system rather than a linear one, as it is watching Life playing out in the plane that people relate to.
It is the lifelike nature of the game that captures people's attention, and although imitating life wasn't really the goal, in a way, finding artificial life was. "I believe that if you have a large enough configuration you will see evolution in the plane," says Conway. "What would happen is every now and then there would be a creature capable of reproducing itself and then they would start to populate the plane. Except the plane is still filled with random junk which might kill some of them. So some of them will be better equipped to survive than others and every now and then they will run into something that hurts and might start a change. Most of these changes will probably be for the worse but every now and then one of these might be for the better and then you know the story. You will probably get evolution happening and you would get creatures that really deserve the name living." He can even imagine that if Life was left to play for a very long time, these creatures might eventually achieve consciousness.
Although the rules are reminiscent of those found in real life, Conway's intention was not to mimic life as we know it. "Many people have produced things of this kind that are closer to real life, such as one with DNA strings in the model. That's counter to my philosophy as it copies the reproductive mechanism that we have. My philosophy is to start with nothing and see if it has its own reproductive mechanism.
"Because I am really not interested in a way in what makes us tick. I have always had this idea that it's rather parochial to be too interested in us. What happens when we meet the Martians, by that I mean somebody out there, another form of intelligent life? There is no obvious reason why they are going to use DNA for their method of storing information, reproducing and so on. They probably have a totally different system.
"I feel that the abstract mathematical things that I am interested in are probably closer to the ones the Martians are interested in. The non-mathematical things that I am interested in, I am very interested in the English language, well, the Martians aren't going to know anything about the English language. And I have been interested in girls (laughs), well, they're not going to be interested in girls, well, in my type of girls! But I think we probably do have some common interests - the common interests are the mathematical ones".

The universal language of mathematics
Although Conway believes that the Martians will also be interested in physics, as we share the same physical universe, the advantage of mathematics is that it does not require expensive equipment to make discoveries. The mind alone is all that is required to study mathematics, and as Conway says, he can "interrogate the abstract universe from an armchair, bath or bed!" And, more than this, the mathematical universe is not just parochial to him. "Though I can sit alone and interrogate that abstract universe, it is not just my universe. It is my colleagues' universe as well. There is a certain stability about it, and I actually believe it is the Martians' abstract universe as well.
"I have always been interested in the abstract world. And the reason is that I don't understand why it's there. I don't understand why theorems don't change. We can still prove Pythagoras's theorem, it's still there 2,000 years after it was found."
Conway doesn't take even the concept of logic for granted. Although he works with logic and proofs every day as a mathematician, he questions whether our axioms of logic are fundamental. "I will be very interested to know what the Martians think," he says. "Do they actually think in the same way as we do? Will their logic be the same?"
The achievement Conway is proudest of is his discovery of a new kind of numbers, the surreal numbers, and it gives him pleasure to think that they will remain in this abstract universe for millennia, just like the theorems of Pythagoras (Donald Knuth wrote an excellent introduction to surreal numbers in the form of a short story - Surreal Numbers : How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness). He discovered the surreal numbers after watching the British Go champion playing in the mathematics department at Cambridge. "I noticed that in Go, near the end of a game it tended to break up as a sum [of games]. That's why I thought I might understand Go a bit better if I developed that theory." Conway went away and did just that and "discovered that some positions behaved like numbers. And then I discovered even more, that if you were playing infinite games, some positions behaved like a new kind of number! And that's how I discovered the surreal numbers."

Playing Go. Picture used courtesy of http://gobase.org/
In a way, Conway's discovery of the surreals parallels the development of Life. He was studying a random system, and as he lived with it he discovered a surprising world. "It has always been a bit of a miracle to me. I started off with the game of Go, and ended up with the surreal numbers, which is a hugely infinite world.
"I think that the Martians have also discovered the surreal numbers somewhere, perhaps not in this galaxy... In that case we would have achieved some sort of intellectual connection. [The alien mathematician would be] the Martian John Conway!" he says. Such a connection would add real value to the abstract mathematical universe by proving it existed independently from humans.
Then again, Conway understands that his whole concept of the shared abstract universe might be wrong. The whole question of mathematical existence, he says "drives me nuts! Maybe the Martians don't have the same notion of mathematical existence as we do, but whatever it is, it will be very interesting!"
About this article

Rachel Thomas is assistant editor on Plus. For this article Rachel interviewed mathematician John Conway.