
It's not unheard of for mathematicians and artists to look at each other with suspicion, and yet numerical relationships underly much form in art and nature. Indeed, many mathematicians are driven by a strongly aesthetic sense of creativity: "There is no permanent place in the world for ugly mathematics", as the mathematician G.H. Hardy once said.
At the Hewlett Packard campus in Bristol, a group of keen researchers have been bringing together the worlds of advanced mathematics and fine art under the umbrella of a Mathematics and Art Project. This project was supported by a Hewlett-Packard initiative, and by the Communications department at HP Labs Bristol, and involved researchers from the Basic Research Institute for the Mathematical Sciences (BRIMS). PASS Maths paid a visit to the project to look at some of their work.
BRIMS

Figure 1: HP Laboratories, Bristol (photo courtesy Hewlett Packard).
Hewlett Packard established the Basic Research Institute in the Mathematical Sciences at the Bristol campus in 1994.
The key research areas in which BRIMS is working (quantum physics, probability theory and dynamical systems) have been chosen to meet the Company's long term business needs, but within this constraint researchers are free to pursue their own interests. The Institute is run rather like a University research group, with support for travel and public meetings, and temporary placements for visiting researchers, postdoctoral assistants and graduate students.
The Mathematics and Art Project

Figure 2: Simon Thomas (left) and Andy Burbanks, Mathematics and Art Project.
The Mathematics and Art Project ("Order in Space") at BRIMS is the brainchild of Neil O'Connell, a mathematician, Simon Thomas, a sculptor, and Bina Shah, the Communications Manager at HP Laboratories Bristol.
While it might seem like a rather fun idea, the project's motivation is very serious. In its vision statement, the founders suggest that
"Mathematics seeks to describe reality by looking at the logical interrelationships between concepts. Through art, we experience reality in ways not directly accessible to reasoning, but which we find intuitively meaningful... Both try to express fundamental "truths" about the nature of reality, seeking structure and symmetry within the complex universe in which we find ourselves."
Simon Thomas

Figure 3: Simon Thomas with one of his sculptures at BRIMS.
Simon Thomas is a professional sculptor with an international reputation. His work has been exhibited widely, has produced numerous commissions for destinations around the world, and has won a number of awards. He was also a founding member of the Mathematics and Art Project at BRIMS.
"I never decided to be an artist", says Simon, "it just ended up that way!" Mathematics implicitly plays a significant part in his work: he describes himself as concerned with "dividing up space and understanding it", and says he has always had "a natural interest in patterns, forms, divisions of space".
Simon says that at school, he enjoyed maths, but that at some point he fell behind. He describes maths as a "hierarchy of knowledge",and says that at some point he missed some "important bits" and "felt lost and helpless. I became defensive".
After secondary school, he went to art college in Portsmouth, finishing with a First Class Honours degree in Fine Art. Three years later, he went to the Royal College of Art to take an MA in Sculpture. It was at the Royal College that he became interested in volumetric curves - "why were they special?". This steered him back towards maths. "I work from my gut, from intuition, but my need to understand space drove me towards maths."
"I asked friends who could help with vectors, and read a useful book called Maths Made Simple. I started working things out with compasses, by trial and error. It was good to have a chance to understand the boundaries of what I was doing." How does maths help? "You can use techniques of geometry to divide space, and there are formulas you can use to simplify calculations. I'm trying to make objects with presence, and there are things to learn - intervals, proportions, like in music."
Simon says that "art has its own logic, and you follow it. Your job is to stay with it. That's creativity." He points out that "the ultimate thing about art is that you play, and play is really important for learning. Maybe it's the same for learning maths - you need to play". Despite talking of play, he is quick to point out that "I work extremely hard. All the time. I never stop thinking about it!"
Hypercones

Figure 4: A hypercone by Simon Thomas.
A mathematical and artistic form that has lately been of great interest to Simon is something that he calls the hypercone.
A hypercone is the spiral-shaped envelope formed when a circle of exponentially decreasing radius is rotated through space, as shown in the sculptures of figures 4 and 5.


Figure 5: Detail from Simon Thomas's hypercone sculpture in the main foyer at HP Labs.
In these sculptures, the "idea" or "Platonic form", as Simon puts it, of a hypercone is represented by a series of concentric rings that have undergone certain rotations. The radii of the rings decrease exponentially and the width of each ring is a fixed proportion of its radius.
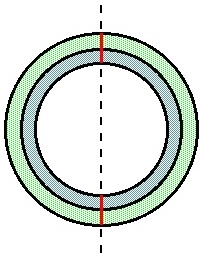
Starting point
Here are two concentric rings lying in a plane, with a common vertical axis running through them.
A hypercone is made of a larger number of such concentric rings (in the abstract, an infinite number, extending endlessly outwards with larger and larger rings and endlessly inwards with smaller and smaller ones).
Each ring in the hypercone is rotated about two axes with respect to its surrounding ring. Using the larger ring as a reference point, let's examine these rotations.
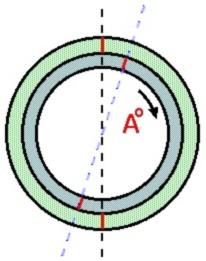
First rotation
Here is the first rotation. The inner ring is still in the same plane as the outer ring, but it has been "turned" in the plane by a fixed angle A (as indicated by the shift in the red alignment marks on the inner ring).
This has offset the original axis (dark dashed line) to produce the inner ring's new axis (pale dashed line).
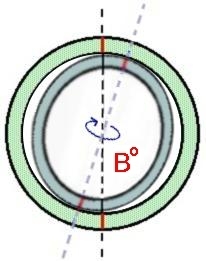
Second rotation
Here is the second rotation. The inner ring is now rotated out of the original plane, by rotating it around the new axis produced by the previous rotation.
The hypercone is now starting to take shape. The next step would be to place another ring of appropriate radius and width inside the inner ring and in the same plane as it, and then perform the same two rotations on this new ring, using the same angle magnitudes A and B.
The abstract idea underpinning these hypercones might be said to be that of a two-dimensional structure (a series of flat concentric rings) being manipulated in such a way that they occupy a volume in three-dimensional space. However, Simon Thomas has explored other artistic variations on the hypercone theme.

Figure 6: Serrated hypercone by Simon Thomas.
Figure 6 shows his "Serrated hypercone", where the plain rings have been replaced by rings with serrated edges to striking effect. The hypercone form here is beginning to look more like a three-dimensional surface than a two-dimensional form moving through three-dimensional space.

Figure 7: Computer model of a hypercone surface.
Figure 7 shows a computer simulation of a three-dimensional hypercone, where a surface has been interpolated around the edges of the rings that form the "skeleton" of the form.

Figure 8: Work in progress on a terraced hypercone at Simon Thomas's studio.
Figure 8 shows work in progress on a terraced interpretation of this surface by Simon Thomas.
Geodesic surfaces
The geodesic dome, invented by R.Buckminster Fuller in the late 1940s, is a structure which uses straight-line segments to approximate the surface of a sphere.
By using triangles of various sizes, Fuller discovered that it was possible to symmetrically subdivide the sphere into a series of bands approximating great circles, or geodesics (hence the name). A great circle is the circle of largest radius that can be drawn around a sphere (like the equator on the earth), and divides the sphere symmetrically into hemi-spheres. [See the Time and Motion article from issue 7 for more on great circles).]
The geodesic dome has gone on to become a popular structure in architecture, primarily because the required strength of its construction elements needs only to increase in proportion to the logarithm of the size of the building, and because it has the highest ratio of enclosed area to external surface area among structures built using only straight edges (i.e. structures composed of polygons).

Figure 9: Detail from Fir Sphere by Simon Thomas.
Geodesic surfaces have been another theme in the work of Simon Thomas. Figure 9 shows his early work Fir Sphere, created in Snowdonia National Park. Again, Simon came at this form "by instinct" rather than by mathematical prescription: as he says of this work,
"Created in a modern forestry plantation, Fir Sphere is an expression of the orders of this environment... At the time, I didn't have a knowledge of spherical division, so in the depths of Snowdonia National Park I somehow rediscovered the orders of Plato and Buckminster Fuller."
Fir Sphere is a comparatively early work, but geodesic surfaces have been a theme in Simon's later work as well.
In the same way that a "flat" hypercone such as that of figures 4 and 5 can be "filled" to a surface such as that in figure 7, the geodesic skeleton of Fir Sphere can form the basis of a filled geodesic surface.


Figure 10: Orb (left) and Marble Orb by Simon Thomas.
Figure 10 shows Simon's pieces Orb and Marble Orb, in form each a textured sphere whose surface has an underlying geodesic structure.
Though this is not immediately obvious to the eye, which sees a "woven" texture, the surface is actually made up of a collection of intersecting cones, aligned in triangles to form a geodesic structure.
Simon says of Orb"This 25cm carving in Crystical developed from knowledge already gained in creating Fir Sphere. Its geometry is based on the Icosahedron and follows the Archimedean division of a spherical surface."and of Marble Orb
"Marble Orb is two thirds of a metre in diameter and uses the same mathematical division of a spherical surface as Orb only a slightly looser knit. This marble carving was useful in better understanding the curved form of the ribbons; there are actually 240 shallow cones intersecting in equal orbit."

Figure 11: CY60 by Simon Thomas.
Figure 11 shows CY60, another variation on the geodesic theme. In this case, the woven-looking surface is actually made up of a collection of intersecting cylinders, again arranged along geodesic principles.
Lyapunov Fractals - A Teaser

This beautiful image was created by Andy Burbanks using a technique based on Lyapunov Exponents, which occur in the study of chaos. In our next issue we'll be including a feature article by Andy, which will explain how some simple maths can lead to the generation of such striking fractal images.
Acknowledgements
Many thanks are due to Neil O'Connell, Andy Burbanks and Simon Thomas for their assistance in preparing this article, and to BRIMS and Hewlett Packard for making our visit possible.