There may not be a Nobel Prize in mathematics, but yet again maths is at the heart of the work recognised in the 2006 Nobel Prizes.
Physics
The 2006 Nobel Prize for Physics goes to two people whose measurements allowed the mathematical models of the Universe's beginning to be tested for the first time. John Mather of NASA, and George Smoot, of the University of California, received the Prize for "their discovery of the blackbody form and anisotropy of the cosmic microwave background radiation". Their work looked at a relic of the early Universe — the cosmic microwave background radiation (CMB) — to try to understand how the Universe began and how galaxies and planets formed. They provided compelling evidence for the Big Bang theory which is now the accepted description of the origin of the Universe.
The CMB radiation that we can see and measure today is much like an echo of the Big Bang. "We're looking back to a time which is between 300,000 and 400,000 years after the Big Bang", says Smoot, "which seems like a long time, but we're 14 billion years after the Big Bang now. So, in human terms it's like looking at an embryo that's a few hours old."
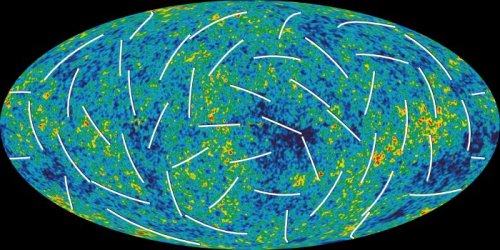
An image of the CMB taken by WMAP. Credit: NASA/WMAP Science Team
Mather's and Smoot's discoveries about the nature of the CMB were based on data from the COBE project — the Cosmic Background Explorer satellite. Mather was a driving force behind the project from its inception in 1974, coordinating the efforts of the over 1000 people involved. And after its launch in 1989, he only needed 9 minutes of data to show that the CMB was a blackbody — a perfect radiator that emits the maximum amount of energy for its temperature. Within minutes of receiving the data it was clear that the CMB radiation had this blackbody form, in fact it is the most perfect blackbody spectrum ever recorded. When the curve for the CMB spectrum was shown at an astronomy conference in January 1990, the results received a standing ovation.
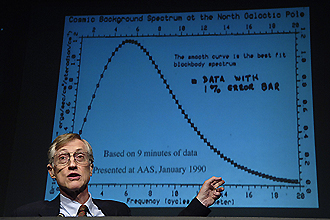
John C. Mather showing some of the earliest data from the COBE Satellite. Photo Credit: NASA/Bill Ingalls.
It is this perfect blackbody spectrum of the CMB, says Mather, that confirms "that the radiation really did come from the Big Bang. There really is not a good alternative explanation for having such a perfect blackbody spectrum." Thus, the data from COBE provided the first opportunity to test the competing mathematical models of the origin of the Universe, and helped take cosmology from a purely theoretical, and in essence mathematical, to a precise science.
The blackbody spectrum revealed by COBE also allowed researchers to develop theories explaining how galaxies and planets were formed. The secret here lies in the temperature of the early Universe, which the Laureates were able to measure. Smoot revealed that this temperature varies by tiny amounts in different directions, confirming the anisotropic nature of the CMB. These extremely small differences — difference of just a hundred-thousandth of a degree — brought with them fluctuations in the density of matter that under the influence of gravity grew into the concentrations that form today's galaxies and planets.
Tiny fluctuations on a quantum mechanical level, their role in shaping the Universe's structure and their reflection in the CBM were predicted by Stephen Hawking and others in the early 1980s. "The statistics of the observed temperature irregularities contain a wealth of information about the nature of the primordial perturbations, as well as the matter composition and geometry of the Universe," says Anthony Challinor, a cosmologist at the University of Cambridge. "By mapping the microwave sky, cosmologists thus hope to answer some of the biggest questions in physics."

George Smoot
With data from COBE, the Laureates were finally able to test the mathematical models of the early Universe, and give new insight into the how it began. While their work might seem to fall into the realms of observational cosmology, the role of mathematics in all this is crucial: without it, there would be no theoretical models to test the data against and no techniques to analyse them in the first place. In an interplay of theory and observation, the quest to understand the origin of the Universe continues. New observations give rise to new theories that explain them and new experiments seek to test those theories in the future (see Plus article Secrets of the Universe — where size really does matter ). Science continues to move forward by looking further and further into the past, to the very beginning of time.
Economics
The 2006 Nobel Prize for Economics went to Edmund S. Phelps of Columbia University, New York, "for his analysis of intertemporal tradeoffs in macroeconomic policy".
Three of the most important goals that any economy strives toward are low unemployment, stable prices (in other words low inflation) and rapid growth. Policy decisions made by governments and central banks can help economies to reach these goals, but often a measure that positively affects one aspect has a negative effect on another. Phelps considered several of these interdependencies and phrased the resulting theory in mathematical models. His results have lead to dramatic changes in economic policy.
During times of low unemployment, workers are in demand and companies need to offer higher wages to attract employees. This in turn drives up prices, leading to a higher rate of inflation. Conversely, high unemployment keeps wages and inflation down. During the 1950s and the 1960s the New Zealand economist A.W. Phillips seemingly verified this simple relationship by conducting a statistical analysis of real data collected in the UK between 1861 and 1957. The result of his research is the Phillips curve shown below, in which the rate of inflation is plotted against the unemployment rate.
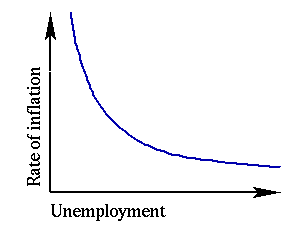
The Phillips curve
According to the curve, the price for a rise in employment is a predictable rise in the rate of inflation. This presents policy makers with a clear-cut basis for their decisions: choose between low inflation and high employment according to preference. However, doubts about the validity of the Phillips curve lingered, since it expressed a purely statistical relationship. Its various aspects, including the fact that there is a predictable tradeoff, could not be backed up by any economic theory.
Phelps applied himself to this problem in the late 1960s by analysing in more detail the wage and price-setting behaviour of businesses. He found that, since businesses do not generally have perfect information about the state of the economy, their decisions are based on expectations and beliefs, as well as on hard information. This led him to devise an equation in which the rate of inflation does not only depend on the rate of unemployment, but also on expectations of future inflation. This model is now known as the expectations-augmented Phillips curve.
It wasn't until some years later that Phelps's theoretical model was confirmed by real data and generally accepted. "In the 1970s," he says, "the Federal Reserve Bank in the United States embarked on policies that led to appreciably higher rates of inflation, with the thought that that was a way of escaping from the fall of employment that had occurred early in the 1970s, and it seemed not to work. And that was probably the decisive moment for this theory."

Edmund Phelps
Contrary to the Phillips curve, Phelps's theory implies that there is no one-time tradeoff between the rate of inflation and unemployment. Since a change in the rate of inflation feeds back into the model in the shape of a change in expectations, the process is a lot more complicated than the original curve stipulated. In some situations keeping employment at a certain level may even cause inflation to rise continually, eventually reaching unacceptable levels.
In the long run, however, an economy will approach an equilibrium unemployment rate, at which the actual rate of inflation equals the expected rate of inflation. It is this equilibrium rate that today guides the policies of most central banks and governments.
Another issue in which tradeoff decisions are central is that of future growth. How much capital should the current generation save in order to ensure the welfare of future generations? Questions like these are particularly acute, since many countries in the developed world have committed themselves to pay out vast amounts of money in pensions between 2020 and 2050. In this context, Phelps takes a Golden Rule approach: "Do unto others as you would have them do unto you". In economic terms, this translates to the idea that the level of consumption should be the same for all generations.
Phelps showed that in order to achieve the Golden Rule target, the rate of savings (as a fraction of national income) must be high enough to ensure that the rate of return of the savings equals the rate of growth of the economy. Interestingly, Phelps also showed that his Golden Rule approach can be generalised to research and development, as well as education: for an optimal outcome the rates of return of investment in these should equal the growth rate. His work also emphasises that better education helps the spread of technology within an economy, a fact that has important implications on poorer countries' quests to catch up with richer ones.
Although Phelps's results are mainly based on theoretical considerations, they have since been borne out by happenings in the real world. Just as in cosmology, economics advances in a delicate interplay between theory and observation — and maths is the language of both.
Further reading
- Read more about cosmology and the origins of the Universe in our special issue celebrating Stephen Hawking's 60th birthday
- Read more about the maths behind the economy in the Plus article Graphical methods III.
- Read more about this and previous Nobel prizes on the Nobel site and on Plus