Three mathematicians working in the USA have come up with a new way for soap to behave. Their new minimal surface is an infinitely twisted version of a plane with a handle sewn on.
The special thing about a film of soap spanning the area within a frame — like the plastic frames used to blow soap bubbles — is that it minimises the amount of soap needed to do just that. There are no unnecessary bulges or bumps, because the same pressure acts on each side of the film's surface.
In an ordinary soap bubble wand, the soap film that forms within the plastic frame is flat, and it is clear that the flat Euclidean plane is a minimal surface in the sense that it covers a least amount of area. But what if you start twisting the frame? How will the soap behave then? This question has fascinated mathematicians for centuries, and it was in the 1770s that French mathematician and general Jean Meusnier came up with a minimal surface called the helicoid, which is also the basis for the latest discovery.
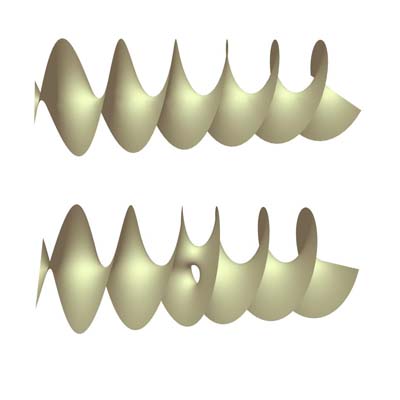
An ordinary helicoid on the top and a genus-one helicoid on the bottom. This image is reproduced here with the kind permission of Matthias Weber.
As the name suggests a helicoid has a lot of twists, in fact there are an infinite number of them; the surface looks a bit like the ramp of an infinite storey car park. A helicoid can be constructed by twisting the plane infinitely many times around a line of your choice within the plane. Any helicoid is given by Cartesian co-ordinates $(x,y,z)$, with $$ x= r cos(t),$$ $$y= r sin(t), $$ $$z= a t,$$ where $r$ and $t$ range from plus infinity to minus infinity, and $a$ is a fixed positive number describing how tightly the helicoid is wound. There is one helicoid for each $a$. It's easy to see that you can deform a helicoid into the plane without jerks or jumps by letting $a$ decrease to zero. You'll go through a range of helicoids, one for each $a$, and finally end up with a surface with co-ordinates $$ x= r cos(t),$$ $$y= r sin(t), $$ $$z=0,$$ which is simply the plane represented by polar co-ordinates.
Since it is made out of the plane, a helicoid has no boundary: an ant walking around on it will never fall off an edge (mathematicians say it is a complete surface). The way the plane has been twisted means that the helicoid does not intersect itself. But its most important property concerns its curvature. Take any point P on the helicoid and draw all the curves on the surface that pass through it. Now if the surface has a bump at P, then every curve has to follow that bump, so we can measure the surface's bumpiness — or lack of it — by measuring how deformed each curve is at P. In this way, we can find a curve that is least deformed at P and a curve that is most deformed. The average of their curviness is called the mean curvature of the surface at P. For the helicoid, you can prove that the mean curvature is zero at every point — meaning that there are no unnecessary bumps or bulges. This zero mean curvature condition is the defining property of a minimal surface.

For more than 200 years, the helicoid was the only known complete minimal surface that can be made by twisting a simple shape. But now the mathematicians Matthias Weber from Indiana University, David Hoffman from Stanford University and Michael Wolf from Rice University have found a second: the genus-one helicoid. The underlying shape is a flat plane with a handle sewn onto it, similar to the handle on a coffee cup. Like the helicoid the handled plane is twisted infinitely many times, only now the surface contains a hole arising from the sewn-on handle. "Until recently, most people would have guessed that any attempt to sew a handle onto a helicoidal soap film would have destroyed the soap film, even theoretically," says Michael Wolf.
It is not quite true to say that the genus-one helicoid is a recent discovery. Hoffman and his co-workers found it as early as 1992, but it took over ten years to prove that it really looks the way they thought it did. This proof is over 100 pages long, but a short version of it has now been published in the Proceedings of the National Academy of Sciences.
And what's the use of a helicoid with a handle? As yet, its discoverers can't think of any direct applications. The new result simply shows that a soap film can behave in ways that were thought impossible before. And anyway, a lack of applications has never stopped a pure mathematician: several millennia of mathematical experience have shown that what seems like pure intellectual indulgence today, may come in extremely useful a few decades or centuries later.
Further reading
- Look at some beautiful minimal surfaces in Matthias Weber's minimal surface gallery.
- Find out more about minimal surfaces on Wikipedia.
- Read the Plus articles Imaging maths - Inside the Klein bottle and Double bubble is no trouble.
- If you are brave, have a look at the (very long) original paper An embedded genus-one helicoid.