Protests against the Iranian election results on the streets of Teheran in June 2009. Photo: Shahram Sharif.
Did Mahmoud Ahmadinejad really win a landslide election on the 12th of June 2009? Many believe that he didn't, but only a full election re-run scrutinised by independent observers would bring absolute certainty. With this possibility thoroughly off the cards, as the Guardian Council has made clear, some analysts have had a long and hard look at the figures released by the Iranian government, to see if they reveal evidence of fraud.
A recent study, edited by Professor Ali Ansari of the Institute of Iranian Studies at the University of St Andrews and of the London think tank Chatham House, compared the official election results with census data collected in 2006 and the election results from 2005. The study found that, if the government figures are to be believed, then two provinces saw a turnout of over 100%. What's more, Ahmadinejad seems to have managed to win over a substantial number of people who had previously supported his fiercest opponents. Previous variations in turnout between provinces, so the study points out, have suddenly disappeared in this election. And those provinces that saw the largest increase in turnout did not correspond to those with the largest swing towards Ahmadinejad, throwing doubt on the argument that the landslide was down to the increased number of people who made their way to the ballot box in this election. Ahmadinejad's supporters have dismissed the study, pointing to pre-election opinion polls which, they say, heralded the swing in favour of Ahmadinejad, and putting the turnout of over 100% down to voters voting outside their home district.
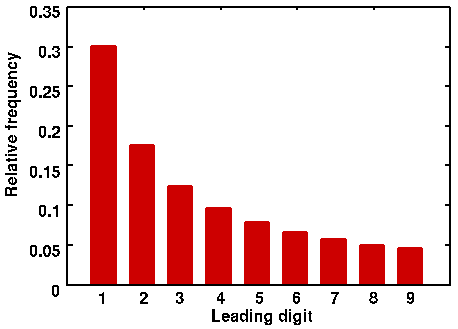
The proportional frequency of each leading digit predicted by Benford's Law.
Ansari's study is based on straight-forward totting up of numbers: it's easy to understand and, given its high-profile origin, has been widely reported. But there are also more subtle statistical tests for fraud. One of these, which has been applied to the Iranian election results by Boudewijn Roukema from Nicolaus Copernicus University in Poland, is based on a simple, but surprising, numerical fact. If you take a list of real-life data, for example the lengths of the world's rivers, an MP's expense claims, or the number of votes cast in electoral districts, then around 30% of these numbers will start with the digit 1, 17.6% will begin with a 2, 12.5% with a 3, and so on, down to the digit 9, which only heads up around 5% of the numbers. Contrary to intuition, the distribution of leading digits is heavily skewed towards 1 and decreases steadily as you go up to 9.
This may make you want to re-consider your lottery numbers, but don't go running off to the newsagent just yet. The curious fact, known as Benford's law, doesn't work for truly random sets of data, in which each digit is equally likely to come first, as intuition would suggest. Neither does it work for highly constrained sets of numbers, for example the heights of people measured in metres, which are unlikely to start with anything greater than 2. Benford's law only works for sets of numbers that are neither too random, nor too constrained. And this is where the potential for fraud detection lies: if the numbers you're looking at should fall into the Benford class, but it turns out that their leading digits don't follow the predicted distribution, then there is evidence that the numbers have been artificially constrained, or that the list has been tempered with in some way. (To find out why Benford's law works, read Plus article Looking out for number one.)

Mahmoud Ahmadinejad. Photo: Daniella Zalcman.
Roukema applied the Benford test to the total number of votes cast in each of Iran's 366 voting districts. The numbers did indeed follow the Benford distribution, but they diverged from it when he split the results between the candidates: the number of votes cast for the candidate Mehdi Karroubi began with a 7 in 41 of the 366 districts. This is almost twice the figure predicted by Benford's law. Roukema calculated that the probability of such a divergence occurring by chance is less than 1%. He also observed that three of the 41 non-Benford districts happened to be among those with the highest populations, in which Ahmadinejad performed especially well. This could be interpreted as evidence that the votes for Karroubi in these districts were tempered with in favour of Ahmadinejad.
The problem with looking at Benford's law for first digits is that, just like the heights of people, the sizes of voting districts may naturally fall within a certain range, so that the law doesn't apply. If, for example, many districts contain between 20,000 and 30,000 voters and see a turnout of around 80%, then a candidate with around 30% of the vote across districts will achieve mostly totals beginning with a 5 or 6. Political scientist and statistician Walter R. Mebane from the University of Michigan used an ingenious way around this problem by considering the second, rather than the first, digits in the totals of votes cast. Ignoring the first digit gives lists of numbers that are not subject to the size constraint and should therefore follow Benford's law. Mebane found that when looking at vote totals for whole towns, the second digits obligingly followed the law's prediction. But a different picture emerged when he looked at the data from individual ballot boxes: here, the second digits for all four candidates except Ahmadinejad's main rival Mir-Hossain Mousavi diverged significantly from the Benford distribution.

Mir-Hossein Mousavi, Ahmadinejad's main opponent. Photo: Mardetanha.
One allegation that has been made against the Iranian election is that many ballot boxes were sealed before opposition representatives had a chance to inspect them. This would give fraudsters the chance to add extra votes for Ahmadinejad (for example by "tombstone voting" — casting votes for dead people), throw away votes for other candidates, or shift them towards Ahmadinejad. One indication of such tempering is when a ballot box contains an unusually low or high proportion of spoilt ballot papers — for example, adding fake votes, or accepting invalid votes in favour of your preferred candidate that should have been discarded will decrease the proportion of invalid votes, while invalidating legitimate votes for other candidates will increase it.
It therefore makes sense to check if the divergence of the second digits from the Benford distribution is related to the proportions of invalid votes in the ballot boxes. Mebane did just that and did indeed find a pattern: in the ballot boxes for which the second digit counts for candidates Karroubi and Rezaei differed significantly from the Benford distribution, the proportion of invalid votes was below a certain theshold. If the Benford test has really spotted fraud, then the boxes involved in the fraud were those with an invalid proportion below this threshold. The divergent second digits for Ahmadinejad also fell within this range.
Mebane then had a look at how the support for the various candidates fared in relation to the proportion of invalid votes. He found that for boxes within the suspicious range of invalid proportions support for Ahmadinejad soared, while support for Karroubi and Rezaei decreased sharply. Outside the suspicious range, the support curves for all candidates flattened out. In other words, the Benford test suggests that fraud did indeed occur at some polling stations, which drove down the proportion of invalid votes in affected boxes and raised support for Ahmadinejad. "The ballot boxes that typically have substantial margins for Ahmadinejad over Mousavi," says Mebane, "are all in the range of invalid vote proportions that, [as] the Karroubi and Rezaei second digits strongly suggest, are affected by fraud. Without the [...] fraud, this analysis suggests, the election outcome should have been at least a runoff between Ahmadinejad and Mousavi."
"Lies, damn lies, and statistics," is the likely response from Ahmadinejad supporters, and they have a point. As Mebane points out, his results don't provide conclusive proof that fraud actually occurred, they only provide supporting evidence. It's possible that Ahmadinejad did win the election through a massive swing in his favour, and it takes political rather than statistical judgment to assess whether such a swing was likely to occur. What statistical tests like Benford's law can do, however, is show up patterns and relationships in sets of numbers that human judgment alone would not be able to pick out. So next time you fiddle your expense claims, tax return, or even an election, take care with those leading (and second and third...) digits.
This story was inspired by George Szpiro's piece for the Swiss newspaper NZZ am Sonntag.
Further reading
- Ali Ansari's report can be downloaded from the Chatham House website;
- Boudewijn Roukema's article is available on arXiv.org;
- And Walter R. Mebane's study is available on his website. In this study Mebane also applies other statistical methods to the Iranian election results.