
Premier league team Everton may have just replaced manager Walter Smith with David Moyes; however, next time they get fed up with a manager's performance, they might consider hiring a mathematician instead.
Operational researchers Mike Wright and Nobuyoshi Hirotsu from Lancaster University have modelled a soccer match as a Markov process. This type of probabilistic model is used to describe a system which at any point in time is in one of a set of defined states, and where the current state of the system only depends on the immediately previous state.
Their model approximates a match as a series of transitions between four states: team A scores a goal, team A is in possession of the ball, team B is in possession of the ball and team B scores a goal. When a player loses possession of the ball or a team scores a goal, the match moves between these four states. A probability can be assigned to each transition, for example, the transition rate between possession and scoring a goal for team A depends on how many goals are scored per minute of possession by team A.
The model can be fully described by specifying the transition probabilities:
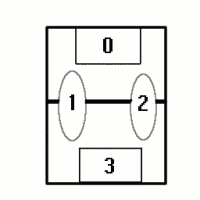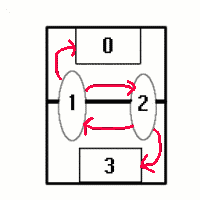 Only four of the transition probabilities (in red) will ever vary |
|
Some of these transition probabilities are the same for every match. For example, when team A scores a goal the ball will automatically go into possession of team B when one of their players kicks off from the centre of the field, so this transition probability will always been 1. By estimating some of the probabilities that vary between matches (highlighted in red above), Wright and Hirotsu are able to solve the differential equations governing the probability distributions for how many goals will be scored or league points won at any point in the game. These calculations take into account the current state of the game, the leading margin and how much time is left in the match.
For their first pass at estimating the probabilities involved, the researchers used match statistics from the English Premier League '98-'99 season published in the Carling Opta Football Yearbook. They counted the number of times the game moved from state 1 to state 2, that is, that the ball moved from possession of team A to team B, by adding up the recorded statistics for "pass to opposition player", "cross pass to opposition player", "dribble the ball lost" and "distribution to opposition player by the goal keeper" in a match. Dividing this by the total time team A were in possession of the ball (also estimated from the yearbook stats) they estimated a12, the probability of possession of the ball changing from team A to team B.
a12 = (the number of times the ball moves from possession of team A to B) / (total time that team A had possession of the ball)
But analysing past matches is not their real goal - they care more about modelling games that are yet to be played. Building on past research which provided methods for estimating home ground advantage and the offensive and defensive capabilities of individual teams, they are able to use data from previous matches to estimate the transition probabilities for a match yet to be played between any two teams.
For example, the transition probability a21 (of possession of the ball moving from team B to home team A) depends on the home ground advantage (in team A's favour), the capability of team A for gaining possession and the tendency of team B to lose possession.
Not only can Wright and Hirotsu estimate the transition probabilities for a particular match played between teams A and B, but also, given the relevant data, for team A playing with certain substitute players and certain strategies. This then means that at any point in the game, they can plug the current score, time left and possession into the probability distributions for goals scored and league points won for each version of the match, to advise when is the best time to make a substitution or to change strategies.
Of course, "any results should only be used as a rough guideline", say the researchers, "since there are many other factors involved in a decision to make a substitution or change formation [such as] considerations of form, fitness, pitch conditions and player availability". So perhaps David Moyes' job is still safe for some time yet.
Mathematically speaking

Meanwhile, sports commentators are often the fans' only live link to the game. So obviously a commentator's voice and how it is used will have a significant effect on fans' enjoyment.
A team of speech experts have developed a formula for rating a person's speech, by analysing the way eight sports commentators spoke and how audiences reacted to them:
\begin{eqnarray*} Speech Quality & = & Pitch - \frac{Overall Loudness}{2} + (2 \times Loudness Variability) \\ & + & \frac{Rate}{2} + ( 1.5 \times Tone) - \frac{Constriction}{2} \end{eqnarray*}
The formula takes into account a number of aspects of a person's speech patterns, including pitch, loudness, and speed. Most of us would score around 21.
The study highlighted how these factors affected the commentary of eight UK radio and television commentators. Barry Davies "used rhythm and tone to project excitement", as did Jon Champion, who built drama using rhythm and rising volume, while Clive Tyldesley conveyed emotions by squeezing and constricting his voice.
Of the eight commentators, the study found that John Motson had the most ideal voice for sports commentating. He has double the vocal range, speaks twice as fast, and can speak both louder and softer than someone with an average speaking voice. Motson scored 6 for pitch, 2 for overall loudness, 6 for loudness variability, 4 for rate, 6 for rhythm, 4 for tone and 2 for constriction, giving a total score of 30.
And the fans agree, with a third of those surveyed voting Motson as their favourite football commentator, saying he inspired the most trust, enthusiasm and excitement.