September 2002
Mathematical Misfits - two-dimensional
Take a square of sidelength 1; it has area $1 \mbox{ unit}^2$. The biggest circle that can fit inside has diameter 1 and area $\pi\times (0.5)^2 = \pi/4 \mbox{ units}^2$. \par The area of this circle divided by the area of the square containing it is $\pi/4$. \par Now we fit the largest possible square inside that circle of diameter 1. We use Pythagoras' Theorem to find its sidelength $d$. \begin{eqnarray*} 2d^2 & = & 1;\\ d & = & 1/\sqrt{2}. \end{eqnarray*} The area of this square is $1/2 \mbox{ units}^2$. \par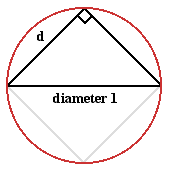
The area of this square divided by the area of the circle containing it is $0.5/\left(\pi/4\right) = 2/\pi.$ \par Since $\pi/4 > 2/\pi$, the round peg fits better in the square hole than the square peg fits in the round hole.
Go back to the main puzzle page