

Who gets the trophy? Image: Jameboy.
On May 22nd 2009 the English Premier league had ten more matches left to play, with West Bromwich Albion at the bottom of the league with 31 points, and Manchester United at the top with 87 points. The bottom three teams would be relegated: West Brom were certain to be one of them, but four teams could possibly join them. ManU were certain to end up the top team and so were not expected to play their strongest team in their away match against Hull City, who were one of the teams up for relegation and so had everything to play for.
The BBC Radio 4 programme More or Less had heard of the work we had been doing on modelling European football results, and they asked us to produce predictions for these final ten matches using a statistical method that could be explained on the radio. Quite a tricky challenge, particularly knowing that the predictions would be announced before the matches and then afterwards compared to what really happened and how well other pundits did. But using some basic probability theory we can quite easily produce a reasonable probability for all the possible results of a game.
We can start by looking at the state of the league on May 22nd 2009, with goals for and goals against.
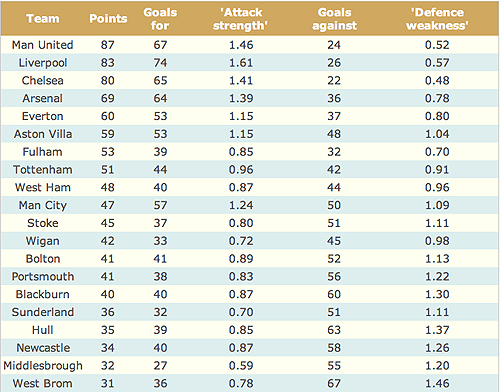
The Premier League table on May 22nd 2009 after 37 games each.
The average number of goals scored, and therefore also the average number of goals conceded, is 46. If we divide the number of goals scored by 46, we get a measure of the attack strength of a team: Arsenal's 64 goals divided by 46 gives 1.39, which shows they have scored 39% more goals than average. If we divide the number of goals conceded by 46 we get a measure of defence weakness: Stoke City's 51 conceded goals divided by 46 gives 1.11, which shows they let in 11% more goals than average.
We also need two other pieces of information: the average number of goals scored per match by a home team is 1.36, while for an away team it's 1.06. Now suppose we want to predict the result of Hull vs Manchester United. We start by estimating how many goals Hull will score. They are playing at home, so if they were an average team, we would expect them to score 1.36. But they are not average: over the season they have scored only 85% of the average number of goals, and so their attack strength is 0.85. Multiplying up we get 1.36 × 0.85 = 1.16. And their opposition is not average either: ManuU's defence weakness is 0.52, since they have conceded only 52% of the average. So we get a total of 1.36 × 0.85 × 0.52 = 0.60 expected goals by Hull, which does not look too good.
For Manchester United, the baseline is 1.06, the average number of goals scored by an away team. But by the time we adjust this for ManU's attack strength and Hulls' defence weakness, we get 1.06 × 1.46 × 1.37 = 2.12.
But, just like nobody has 2.4 children, nobody scores 2.12 goals — this is only an expected value. It's the average number of goals scored by ManU if the match were played again and again, heaven forbid. But we can use what is known as the Poisson probability distribution to distribute 100% of probability across the possible number of goals. The distribution expresses the probability of a number of events occurring in a given time period, if the average rate of the occurrence is known and the events are independent. Thus we get probability distributions shown in the table below.

The percentage probability of each team scoring a specified number of goals in the match on May 24th 2009, using a simple Poisson model.
So, if the next match follows past performance, there is a 55% probability that Hull won't score at all, and 63% (100 - 25 -12) probability ManU will get at least 2 goals, even though playing away.
To get the probability of an actual result, we might assume that the goals scored by each team are independent, in the sense that if we knew how many ManU scored, it would not give us any additional information about Hull's performance. This is a strong assumption and we'll come back to it in a moment, but it means that to find, for example, the probability of a 0-2 result, which is the most likely outcome, we multiply 55% by 27% to get 15% (55/100 × 15/100 = 0.1485), so even the most likely result is still not very likely!
In fact there tends to be some correlation between teams' results, in the sense that matches have a tendency to be either high or low scoring, which we might call a "pitch effect". Estimating probabilities allowing for correlations is more complicated and requires special software: the bivariate Poisson model is popular and can be fitted using free programs. Yin-Lam Ng, in her Cambridge MPhil in Statistical Science project, fitted models to all major league results in Europe over the last 15 years, and the predictions below are based on the best model found.
Statistical models assume that past performance predicts future results, and do not take into account new factors. For example, Hull City are trying to avoid relegation, Manchester United are conserving their strength having already topped the league, and so it is possible that Hull City may stand a much better chance of winning than the 9% we have given them — some people obviously thought so, as the odds offered by the bookies were more like 2 to 1 against, or a 33% chance of Hull winning.
Below is a table of the four most likely results for each match according to the statistical model.
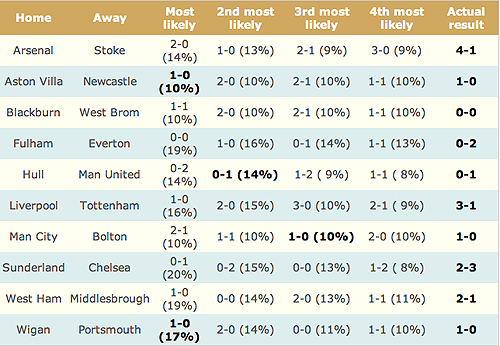
The four most likely results for each match, with their percentage probability according to a bivariate Poisson model.
Note that the highest chance is 20%, and for most matches there's only a around 50% chance that any of these top four results will occur. So it's rather misleading to treat the "most-likely" results as predictions — all this model does is produce (what we hope are) reasonable probabilities. If we add up the probabilities for results that lead to a win/draw/lose we get the probabilities shown below. Some of these become quite high, for example 72% for a home win in the Arsenal-Stoke match, but even these could not be considered as firm predictions.
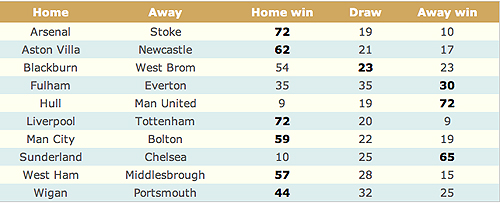
The percentage probability of each result for the final ten matches of the Premier league, based on a bivariate Poisson model. The actual results are shown in bold.
The most likely results were read out on the More or Less broadcast on May 22nd, without any qualifying probabilities, somewhat to our consternation. They were also given on the BBC More or Less website , this time with probabilities (although we mistakenly said the Fulham-Everton most-likely 0-0 prediction with probability 10% whereas we should have said 19%, and Liverpool-Tottenham's most-likely prediction was given probability 10% instead of 16%.)
So what happened? The day of the matches was nerve-wracking, but when the results were announced we were very relieved to find that using our best predictions, we got nine results out of ten right in terms of win/draw/lose, and we also predicted two exact scores: Aston Villa-Newcastle (1-0) and Wigan-Portsmouth (1-0). This was particularly gratifying as Mark Lawrenson, the official BBC football expert, only got seven correct results, and only one exact score.

A contented Alex Ferguson whose ManU are current Premier League champions. Image: Austin Osuide
This is a very good result for statistics! But perhaps a bit lucky — in particular it is very difficult to predict draws and it was rather fortunate that the most-likely 1-1 Blackburn-WestBrom score turned out to be a 0-0 draw, since a draw was not the most likely outcome. One possible advantage of the statistical method is that it is not influenced by emotion. For example, in the Hull-ManU match, Hull was considered as having some chance of a win, and Mark Lawrenson predicted a draw, but we went for a ManU win and were proved correct.
These types of models have been refined over the years and are now used by bookies and sports betting companies, who employ experienced statisticians and make use of the latest computational methods: in particular it is natural to extend our model to allow for a team's abilities to change over the season, and so discount historical evidence to allow recent performance to dominate. And, not surprisingly, they don't tell anyone exactly what they do! One thing you can bet on: simple models like those above will be very unlikely to out-perform the odds being offered by bookies, so you should not use them to spot good bets. We have heard that some people did make money from our predictions, and we have since been approached by people wanting to work with us on sports modelling, but I don't think we will take this up as a sideline — it could be much too engrossing.
About the authors


David Spiegelhalter is Winton Professor of the Public Understanding of Risk at the University of Cambridge.
Yin-Lam Ng was an MPhil student at Cambridge and has now joined Hong Kong Polytechnic University as a research assistant.
David and his team run the Understanding uncertainty website, which informs the public about issues involving risk and uncertainty.